总结
代码
观察过程代码
正确代码
细节代码
来自《啊哈算法》
前言
刚学了树在优先队列中的应用--堆的实现
那么树还有哪些神奇的用法呢我们从一个故事说起----揭秘犯罪团伙
故事
快过年了犯罪分子们也开始为年终奖“奋斗”了小哼的家乡出现多次抢劫事件。
由于强盗人数过于庞大作案频繁警察想调查清楚到底有几个犯罪团伙实在不容易。
不过警察叔叔还是搜集到了几条线索
现在有10个强盗9条线索

1--2表示1号强盗与2号强盗是同伙
3--45--24--62--68--79--71--62--4
规定强盗同伙的同伙也是同伙你能帮警察叔叔查出有多少个独立的犯罪团伙吗
思路
要解决这个问题先假设10个强盗相互不认识他们各自为政每个人都是自己的头只听自己的
之后我们通过警察的线索一步步“合并同伙”
1声明一维数组
申请一个一维数组daddad[1] 1表示1号强盗的头是自己10号强盗的头是10号自己用dad[10] 10表示
2初始化
初始化dad数组当然书里是f数组 令 dad[i] i; 即可

3合并同伙
如果发现两个强盗是同伙那么他俩是同一犯罪团伙但是。。。谁做老大呢
我们假定左边的强盗更厉害些规定一个“靠左法则”比如警察得到的第一条线索是1号和2号同伙
1
所以1号在左边更厉害那么2号归顺1号也就是1号是2号的头头所以dad[2] 1;表示2号强盗的头是1号强盗

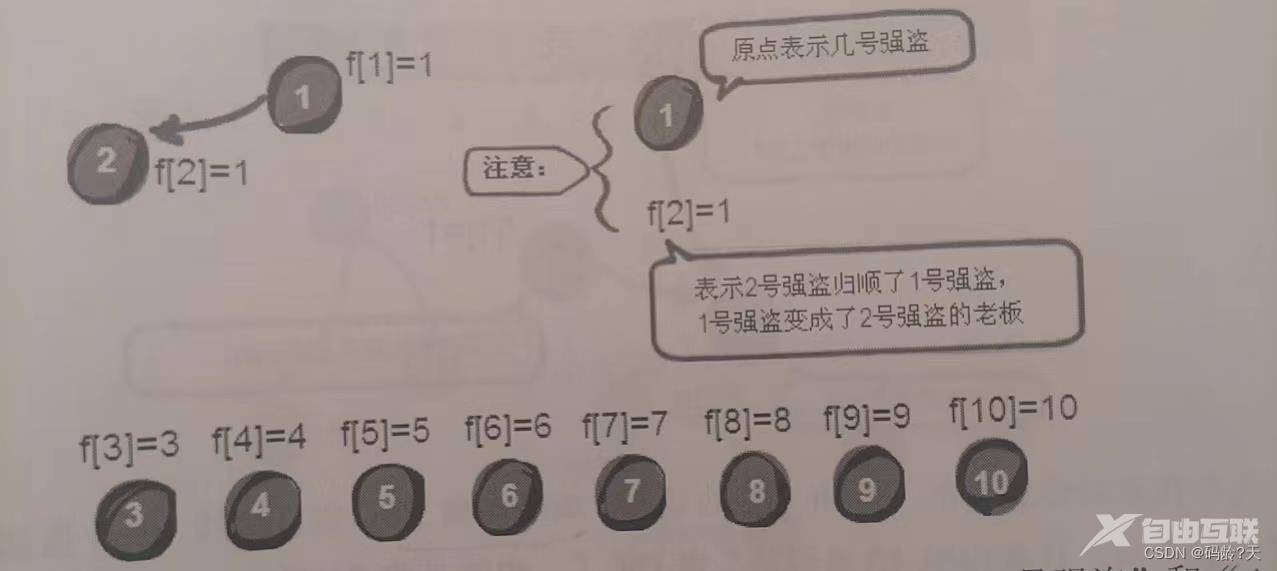
2
第二条线索3--43号强盗和4号是同伙根据“左边的更厉害”4号归顺3号所以 dad[4] 3;
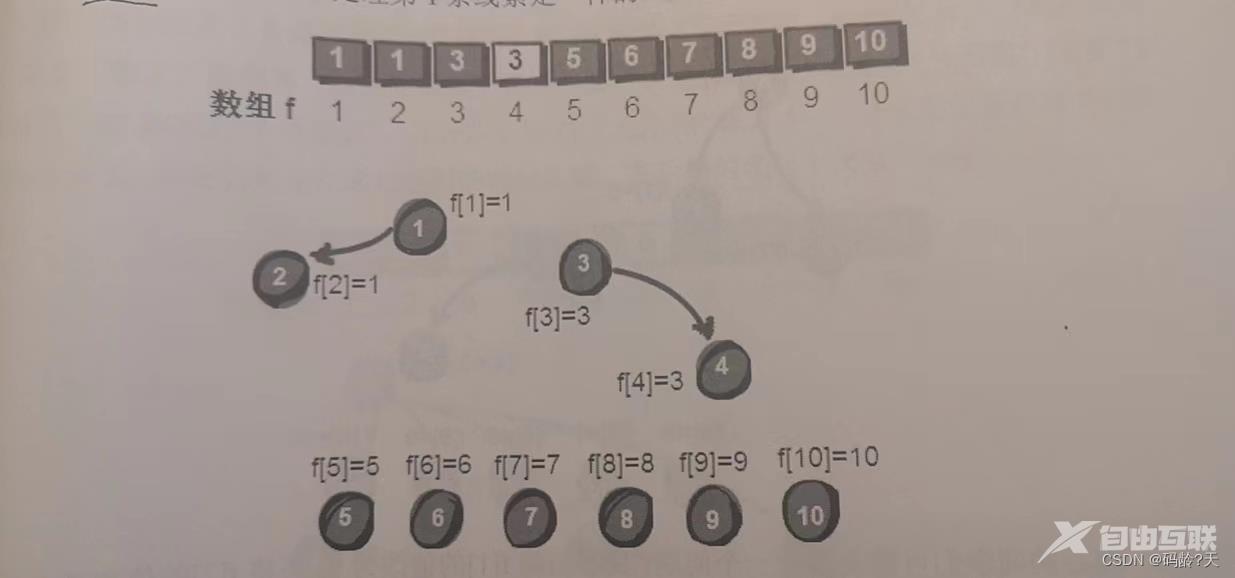
3
第3条线索5--25号和2号强盗是同伙dad[5] 5说明5号强盗的头是自己
dad[2] 1说明2号强盗的头是1号强盗
根据“左边的更厉害”此时应该让2号归顺5号那么“1号强盗”就不干了“你凭什么抢我的人”
于是这俩强盗差点打起来了这让2号为难了2号归顺5号还是继续跟着原来的头1号呢
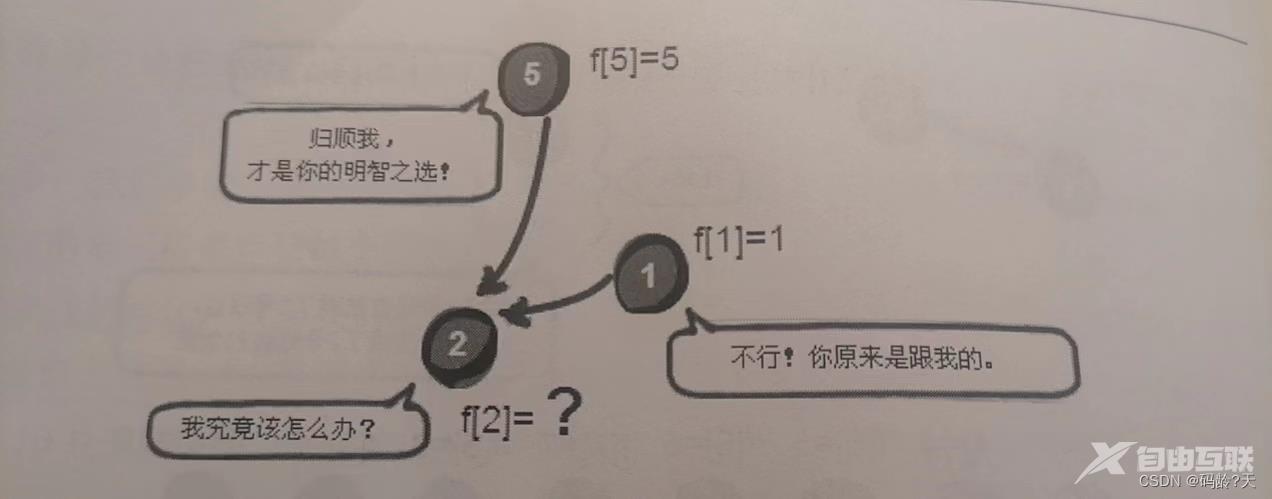
这里我们还是按左边的更厉害的原则5号强盗直接找2号的头1号谈让1号这个老大也归顺他(递归实现)
操作dad[1] 5; dad[2] 5;
为什么在1号这个老大归顺5号后还要再让2号归顺一次呢
这一步不是必须的但会提高后面找强盗最高领导人的速度也就是找树的祖先的速度
否则很容易形成单支树结构一长条。。。极大浪费空间和时间
dad[2] 5; 这看似多余的一步也叫路径压缩不要觉得名字很高大上其实就是一行代码的事
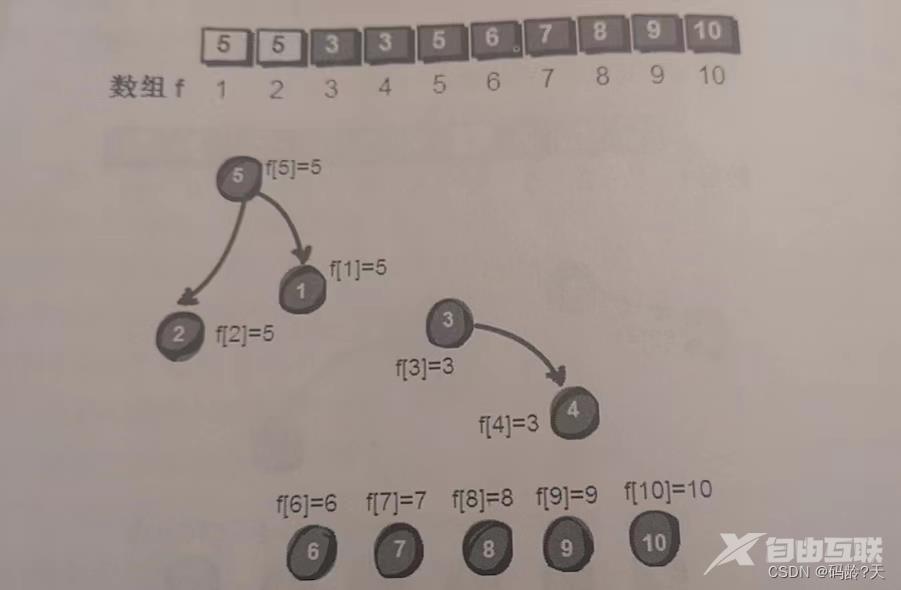
第四条线索
4--6这俩同伙
此时dad[4] 3, dad[6] 6我们让6号强盗加入“3号犯罪团伙”即dad[6] 3;

第5条线索
2--6
此时dad[2] 5, dad[6] 3
我们令6号和他的老大都归顺“5号犯罪团伙”(递归实现)dad[6] 5; 以及 dad[3] 5;
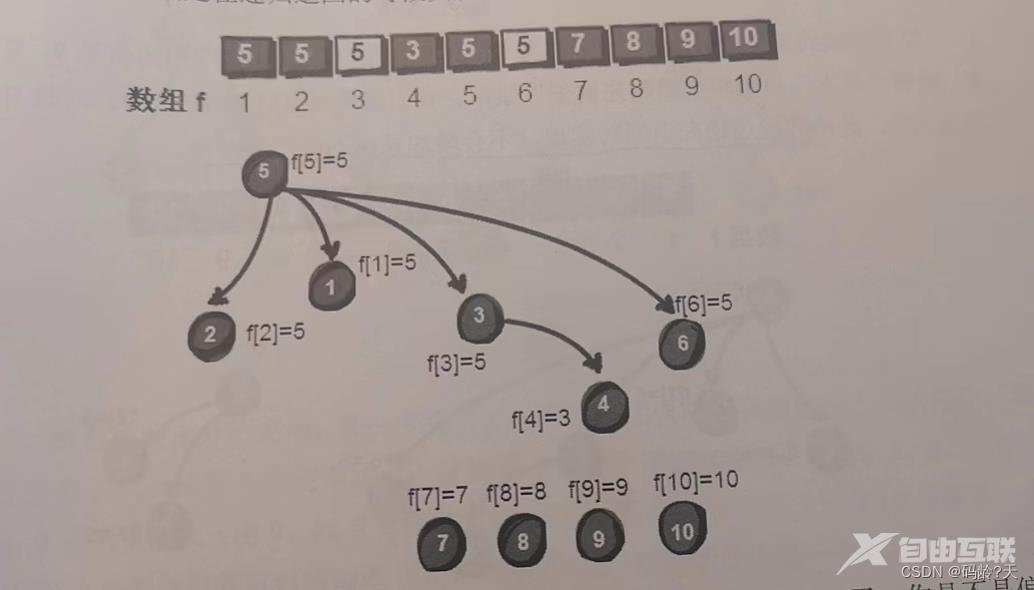
第6条线索
8--7
此时dad[8] 8, dad[7] 7, 让7号归顺8号好了dad[7] 8;
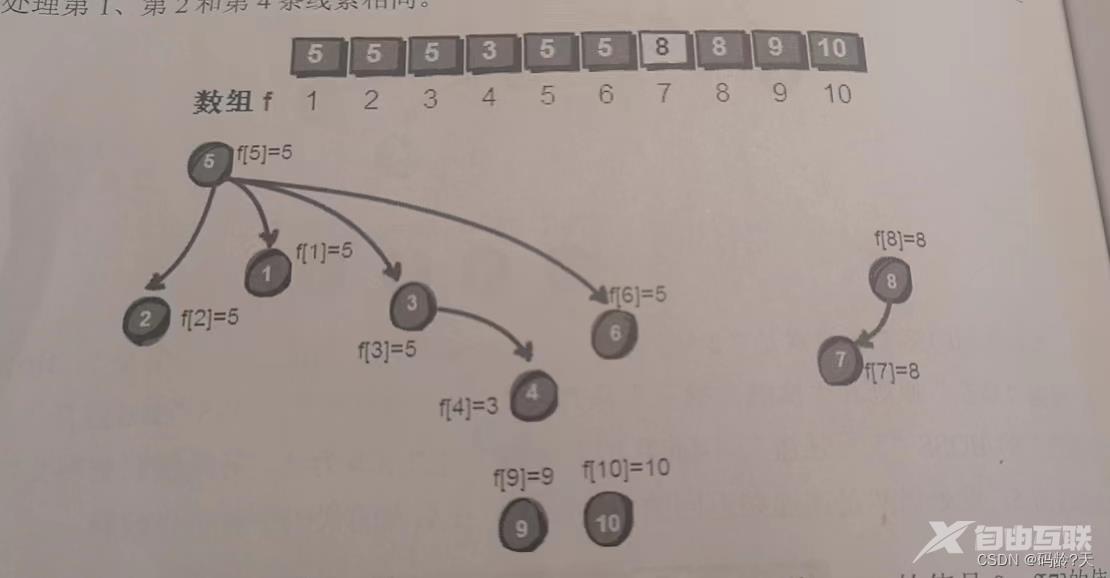
第7条线索
9--7
此时dad[9] 9, dad[7] 8所以8号和7号都归顺9号强盗(路径压缩)(递归实现)
dad[8] 9; dad[7] 9;

除了让7号的老大归顺9号我们还让7号也直接归顺9号这一步叫路径压缩这一步通过递归返回时实现不会增加时间复杂度
第8条线索
1--6
此时dad[1] 5, dad[6] 5已经是同伙了不需要操作
第9条线索
2--4
此时dad[2] 5, dad[4] 3
4号归顺3号3号归顺5号5号归顺自己所以5号是最高领导人
从4号顺藤摸瓜到5号最高领导人的过程就是递归
递归完后dad[4] 5;
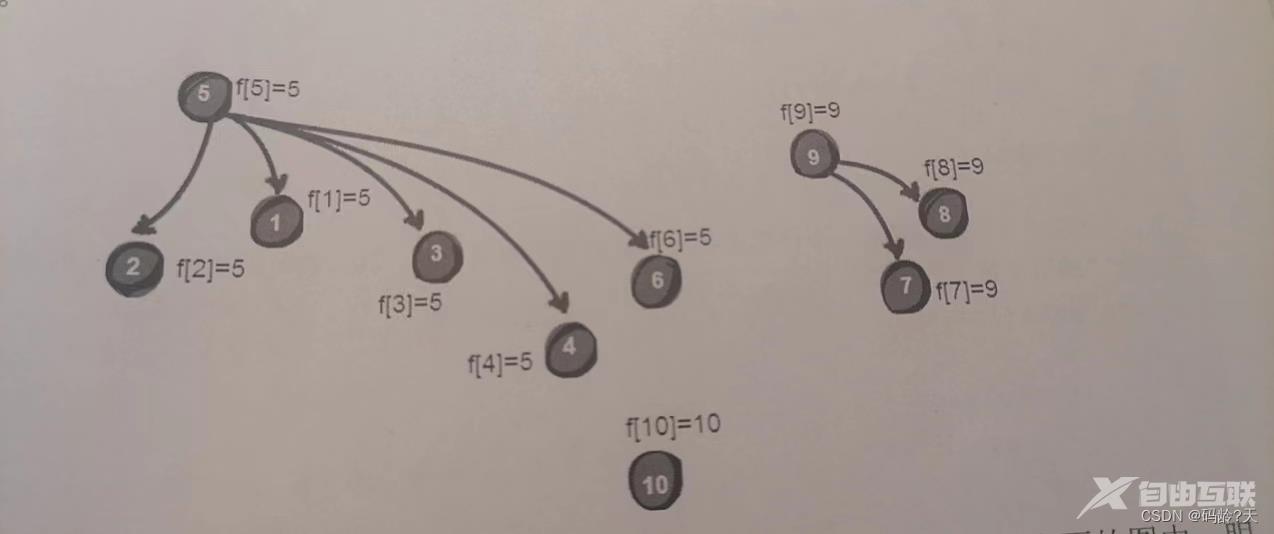
至此所有线索分析完毕那么有多少个犯罪团伙呢
由上图可知3个团伙
5号犯罪集团521346组成
9号犯罪集团987组成
10号犯罪集团10组成
容易知道如果 dad[i] i表示 i 号强盗是一个团伙的最高领导人最后数组dad中
dad[5] 5, dad[9] 9, dad[10] 10所以共3个犯罪团伙
总结

我们刚才模拟的是并查集算法并查集通过一个一维数组实现本质是维护一个森林。
初始森林每个点都是孤立的也就是每个强盗的老大都是自己也可以理解为每个点就是一棵只有一个节点的树
之后将这些孤立的点合并成一颗大树合并的过程就是叫爸爸的过程
叫爸爸的过程遵循“左边更厉害”和“擒贼先擒王”的原则
“擒贼先擒王”也就是先让老大归顺左边的强盗自己再归顺自己再归顺就是路径压缩
补充: 并查集也称为为不相交集数据结构
代码 观察过程代码
#includeusing namespace std;int dad[100];int Find(int x) //不停认老大, 直到顶头上司{if(dad[x] x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] Find(dad[x]);return dad[x];}}void join(int x, int y) //合并两个团伙{//m为x的最高领导人, n为y的最高领导人int m Find(dad[x]), n Find(dad[y]);if(m ! n) //路径压缩dad[n] m; //第2个最高领导人认第1个当老大}int main(){for(int i 1; i < 10; i)dad[i] i; //初始化自己为老大int a, b;for(int i 1; i < 9; i) {cout<<"第"< 为什么第一次没实现路径压缩呢就是虽然团伙总数确定了但是每个人依然跟着自己原来的老大没有跟着顶头上司 原来是代码第18行 m Find(dad[x]), n Find(dad[y]); 应该改成 m Find(x), n Find(y); 否则只是令右老大归顺了左老大但是右小弟没有直接归顺左老大右小弟依然跟着右老大 这样就没起到路径压缩的效果 即使是正确代码《啊哈算法》里也存在BUG不过无关痛痒而已对时间复杂度几乎没影响 #includeusing namespace std;int dad[100];int Find(int x) //不停认老大, 直到顶头上司{if(dad[x] x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] Find(dad[x]); //递归返回return dad[x];}}void join(int x, int y) //合并两个团伙{//m为x的最高领导人, n为y的最高领导人int m Find(x), n Find(y);if(m ! n) //路径压缩dad[n] m; //第2个最高领导人认第1个当老大}int main(){for(int i 1; i < 10; i)dad[i] i; //初始化自己为老大int a, b;for(int i 1; i >a>>b;join(a, b); //合并团伙}int ans 0;for(int i 1; i < 10; i)if(dad[i] i)ans 1;for(int i 1; i < 10; i)cout<<"第"< 上述代码实现了路径压缩但是第7个强盗的老大怎么还是8呢不应该是9吗 因为这种较为简单的路径压缩有一个小小的缺陷 需要第一次先找到祖宗第二次才能对路径上的节点进行压缩而输入9 7前7原来的老大是88的原来的老大也是8当输入9 7后进行join()函数 此时7的老大8号就归顺了9号但7的老大依然是8号没有变成9号需要在下一次递归查找老大时7的老大才变成9号但此时已经没有下次了 当然我们也可以在join()函数的最后重写一次 n Find(y) 就可以实现书里的效果但是不知道这样是否会影响时间复杂度 #includeusing namespace std;int dad[100];int Find(int x) //不停认老大, 直到顶头上司{if(dad[x] x) return x;else {//路径压缩, 将路径上所有点的上级都设置为根节点dad[x] Find(dad[x]); //递归返回return dad[x];}}void join(int x, int y) //合并两个团伙{//m为x的最高领导人, n为y的最高领导人int m Find(x), n Find(y);if(m ! n) //路径压缩dad[n] m; //第2个最高领导人认第1个当老大n Find(y); //重写一次}int main(){for(int i 1; i < 10; i)dad[i] i; //初始化自己为老大int a, b;for(int i 1; i >a>>b;join(a, b); //合并团伙}int ans 0;for(int i 1; i < 10; i)if(dad[i] i)ans 1;for(int i 1; i < 10; i)cout<<"第"<正确代码
细节代码
