6031. 找出数组中的所有 K 近邻下标
给你一个下标从 0 开始的整数数组 nums 和两个整数 key 和 k 。K 近邻下标 是 nums 中的一个下标 i ,并满足至少存在一个下标 j 使得 |i - j| <= k 且 nums[j] == key 。
以列表形式返回按 递增顺序 排序的所有 K 近邻下标。
示例 1:
输入:nums = [3,4,9,1,3,9,5], key = 9, k = 1输出:[1,2,3,4,5,6]解释:因此,nums[2] == key 且 nums[5] == key 。- 对下标 0 ,|0 - 2| > k 且 |0 - 5| > k ,所以不存在 j 使得 |0 - j| <= k 且 nums[j] == key 。所以 0 不是一个 K 近邻下标。- 对下标 1 ,|1 - 2| <= k 且 nums[2] == key ,所以 1 是一个 K 近邻下标。- 对下标 2 ,|2 - 2| <= k 且 nums[2] == key ,所以 2 是一个 K 近邻下标。- 对下标 3 ,|3 - 2| <= k 且 nums[2] == key ,所以 3 是一个 K 近邻下标。- 对下标 4 ,|4 - 5| <= k 且 nums[5] == key ,所以 4 是一个 K 近邻下标。- 对下标 5 ,|5 - 5| <= k 且 nums[5] == key ,所以 5 是一个 K 近邻下标。- 对下标 6 ,|6 - 5| <= k 且 nums[5] == key ,所以 6 是一个 K 近邻下标。因此,按递增顺序返回 [1,2,3,4,5,6] 。
示例 2:
输入:nums = [2,2,2,2,2], key = 2, k = 2输出:[0,1,2,3,4]解释:对 nums 的所有下标 i ,总存在某个下标 j 使得 |i - j| <= k 且 nums[j] == key ,所以每个下标都是一个 K 近邻下标。 因此,返回 [0,1,2,3,4] 。
提示:
- 1 <= nums.length <= 1000
- 1 <= nums[i] <= 1000
- key 是数组 nums 中的一个整数
- 1 <= k <= nums.length
两次循环
class Solution: def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]: n = len(nums) ans = [] for i in range(n): for j in range(max(0, i - k), min(n, i + k + 1)): if nums[j] == key: ans.append(i) break return ans
5203. 统计可以提取的工件
存在一个 n x n 大小、下标从 0 开始的网格,网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ,artifacts 描述了矩形工件的位置,其中 artifacts[i] = [r1i, c1i, r2i, c2i] 表示第 i 个工件在子网格中的填埋情况:
- (r1i, c1i) 是第 i 个工件 左上 单元格的坐标,且
- (r2i, c2i) 是第 i 个工件 右下 单元格的坐标。
你将会挖掘网格中的一些单元格,并清除其中的填埋物。如果单元格中埋着工件的一部分,那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来,你就可以提取该工件。
给你一个下标从 0 开始的二维整数数组 dig ,其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci) ,返回你可以提取的工件数目。
生成的测试用例满足:
- 不存在重叠的两个工件。
- 每个工件最多只覆盖 4 个单元格。
- dig 中的元素互不相同。
示例 1:
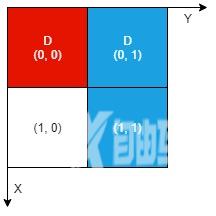
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]输出:1解释: 不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。有 1 个工件可以提取,即红色工件。蓝色工件在单元格 (1,1) 的部分尚未裸露出来,所以无法提取该工件。因此,返回 1 。
示例 2:
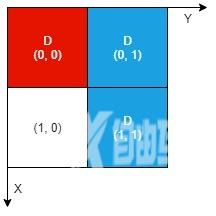
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]输出:2解释:红色工件和蓝色工件的所有部分都裸露出来(用 'D' 标记),都可以提取。因此,返回 2 。
提示:
- 1 <= n <= 1000
- 1 <= artifacts.length, dig.length <= min(n2, 10^5)
- artifacts[i].length == 4
- dig[i].length == 2
- 0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1
- r1i <= r2i
- c1i <= c2i
- 不存在重叠的两个工件
- 每个工件 最多 只覆盖 4 个单元格
- dig 中的元素互不相同
先挖再判断
class Solution: def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int: map = [[0] * n for _ in range(n)] for d in dig: map[d[0]][d[1]] = 1 count = 0 # 注意每个工件最多只覆盖 4 个单元格 for a, b, c, d in artifacts: judge = True for i in range(a, c + 1): for j in range(b, d + 1): if map[i][j] == 0: judge = False break if judge == False: break if judge == True: count += 1 return count
5227. K 次操作后最大化顶端元素
给你一个下标从 0 开始的整数数组 nums ,它表示一个 栈 ,其中 nums[0] 是栈顶的元素。
每一次操作中,你可以执行以下操作 之一 :
- 如果栈非空,那么 删除 栈顶端的元素。
- 如果存在 1 个或者多个被删除的元素,你可以从它们中选择任何一个,添加 回栈顶,这个元素成为新的栈顶元素。
同时给你一个整数 k ,它表示你总共需要执行操作的次数。
请你返回 恰好 执行 k 次操作以后,栈顶元素的 最大值 。如果执行完 k 次操作以后,栈一定为空,请你返回 -1 。
示例 1:
输入:nums = [5,2,2,4,0,6], k = 4输出:5解释:4 次操作后,栈顶元素为 5 的方法之一为:- 第 1 次操作:删除栈顶元素 5 ,栈变为 [2,2,4,0,6] 。- 第 2 次操作:删除栈顶元素 2 ,栈变为 [2,4,0,6] 。- 第 3 次操作:删除栈顶元素 2 ,栈变为 [4,0,6] 。- 第 4 次操作:将 5 添加回栈顶,栈变为 [5,4,0,6] 。注意,这不是最后栈顶元素为 5 的唯一方式。但可以证明,4 次操作以后 5 是能得到的最大栈顶元素。
示例 2:
输入:nums = [2], k = 1输出:-1解释:第 1 次操作中,我们唯一的选择是将栈顶元素弹出栈。由于 1 次操作后无法得到一个非空的栈,所以我们返回 -1 。
提示:
- 1 <= nums.length <= 10^5
- 0 <= nums[i], k <= 10^9
分类讨论
class Solution: def maximumTop(self, nums: List[int], k: int) -> int: # 如果只有一个元素,那么只能拿出再放回,因此 k 不能是奇数 if (len(nums) == 1 and k % 2 == 1): return -1 # 操作为 0 或者 1 if k <= 1: return nums[k] # 操作数大于长度,因此可以全部拿出,然后乱搞,最后一次把最大值放进去 if (k > len(nums)): return max(nums) # 可以拿出除最后一个的所有,然后返回最大值 if (k == len(nums)): temp = nums[:k-1] return max(temp) # 可以全部取出 k 个或者 取出 k - 1 个返回最大值 temp = nums[:k-1] return max(max(temp), nums[k])
6032. 得到要求路径的最小带权子图
给你一个整数 n ,它表示一个 带权有向 图的节点数,节点编号为 0 到 n - 1 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi, weighti] ,表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。
最后,给你三个 互不相同 的整数 src1 ,src2 和 dest ,表示图中三个不同的点。
请你从图中选出一个 边权和最小 的子图,使得从 src1 和 src2 出发,在这个子图中,都 可以 到达 dest 。如果这样的子图不存在,请返回 -1 。
子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。
示例 1:
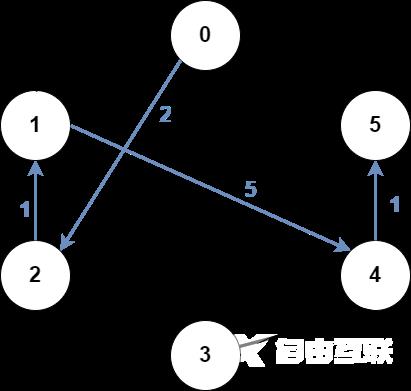
输入:n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5输出:9解释:上图为输入的图。蓝色边为最优子图之一。注意,子图 [[1,0,3],[0,5,6]] 也能得到最优解,但无法在满足所有限制的前提下,得到更优解。
示例 2:

输入:n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2输出:-1解释:上图为输入的图。可以看到,不存在从节点 1 到节点 2 的路径,所以不存在任何子图满足所有限制。
提示:
- 3 <= n <= 10^5
- 0 <= edges.length <= 10^5
- edges[i].length == 3
- 0 <= fromi, toi, src1, src2, dest <= n - 1
- fromi != toi
- src1 ,src2 和 dest 两两不同。
- 1 <= weight[i] <= 10^5
分析
我们可以是a->b->c 或者 b->a->c 或者 a->c and b->c或者 a->x and b->x and x->c 。而且我们可以发现前三种情况是后面一种的特殊情况,那我们只要考虑 a 和 b 通过一个中间点,然后到 c 。中间点可以是 a、b、c 自身。然后就是枚举中间点求最小值就好。
那么我们需要知道 a 到每个点的最小距离,b 到每个点的最小距离,c 到每个点的最小距离。a 和 b 只要搜索就好了,但是 c 到每个点的距离不太好求,如果求每个点到 c 的距离的话复杂度就高了。因此可以考虑再反向建个图,然后 c 开始搜索。
搜索的时候用的 bfs ,但是很无奈,超时了。因为这里有权重,所以我们用 Astar 启发式搜索,用一个优先队列队首元素为当前的最小值。
class Solution: def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int: # 很奇怪,没加这句有个隐藏测试 if len(edges) <= 1: return -1 # 正向图 edge1 = [[] for _ in range(n)] # 反向图 edge2 = [[] for _ in range(n)] for e in edges: a, b, c = e[0], e[1], e[2] edge1[a].append((b, c)) edge2[b].append((a, c)) # dp1[i] 表示 src1 到点 i 的最短距离 dp1 = [1e11] * n # dp2[i] 表示 src2 到点 i 的最短距离 dp2 = [1e11] * n # dp3[i] 表示 dect 到点 i 的最短距离 dp3 = [1e11] * n qu = [] def bfs1 (x: int): dp1[x] = 0 heapq.heappush(qu, (0, x)) while len(qu) > 0: w, x = heapq.heappop(qu) # die'q while w > dp1[x] and len(qu) > 0: w, x = heapq.heappop(qu) for y, w1 in edge1[x]: if w + w1
