典型的存储方式就两种要么是顺序存储利用数组这种机制要么是链式存储利用链表这种机制。
基于二叉树区别于其他树的结构且其最多只有两个孩子结点等特性二叉树可以用顺序存储来实现但这种顺序存储在空间利用率上会有一定的缺陷。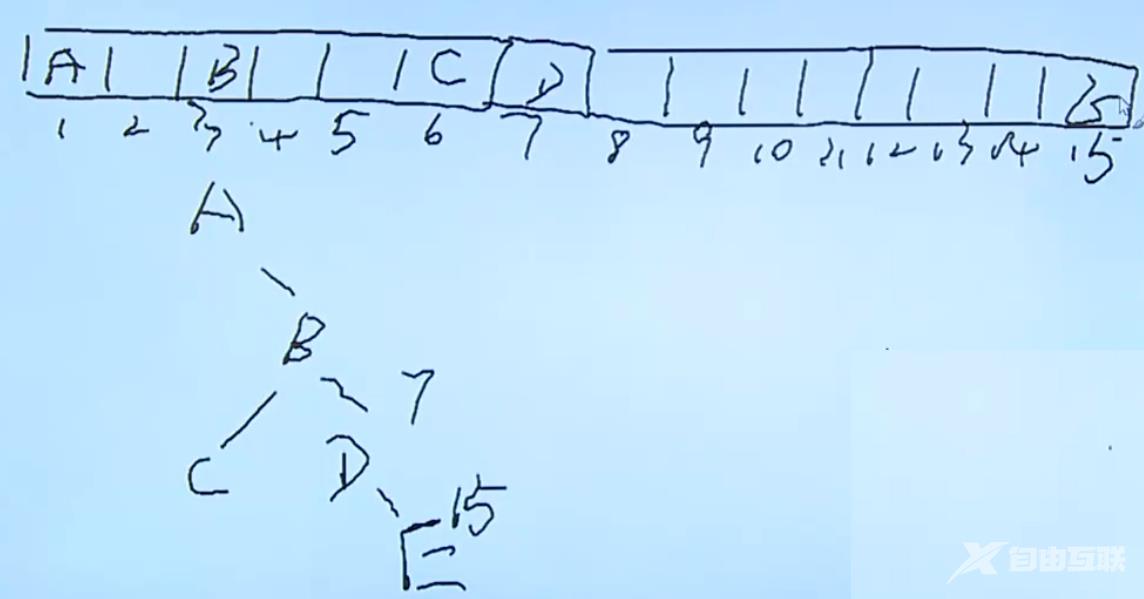 
n层二叉树或者说深度为 n 的二叉树最多有2n - 1个结点。
使用顺序存储利用数组来实现满二叉树和完全二叉树是非常适合的斜二叉树就不合适了。
实现二叉树的最基本的思想就是 “ 递归 ”
这里创建二叉树的规则如下
与当前结点的 id 的值进行比较若比当前结点小就作为当前结点的左子树如果比当前结点大就作为当前结点的右子树。如果当前结点已经有了左子树或者右子树就继续与它的左子树或者右子树进行比较然后进行创建。
具体实现是
在程序中我们会事先把每个要创建的结点的 id 都定义在一个数组中。当然由于第一个 id 之前没有其他的 id无法比较所以我们就直接把它作为根节点。当创建第二个结点的时候就让它与根节点进行比较然后依此进行。
示例如下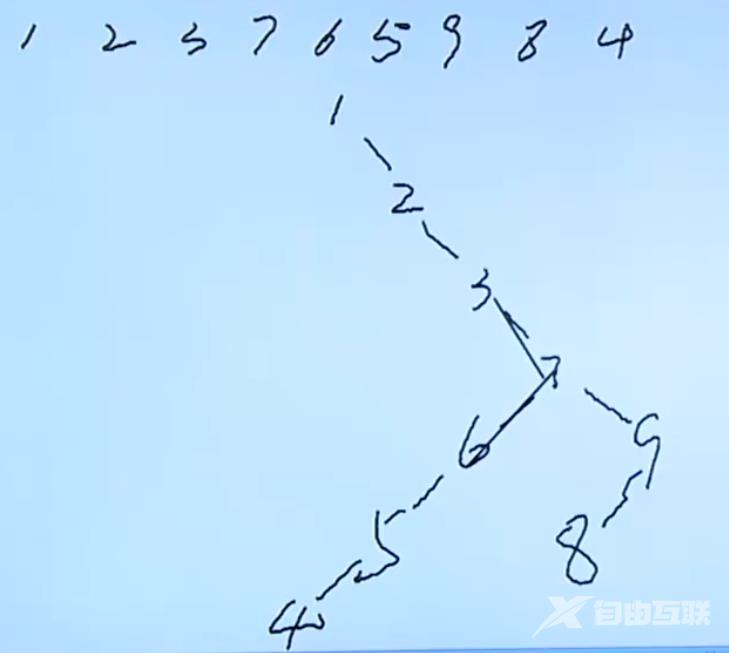 
程序中在二叉树中插入第一个结点的示意图如下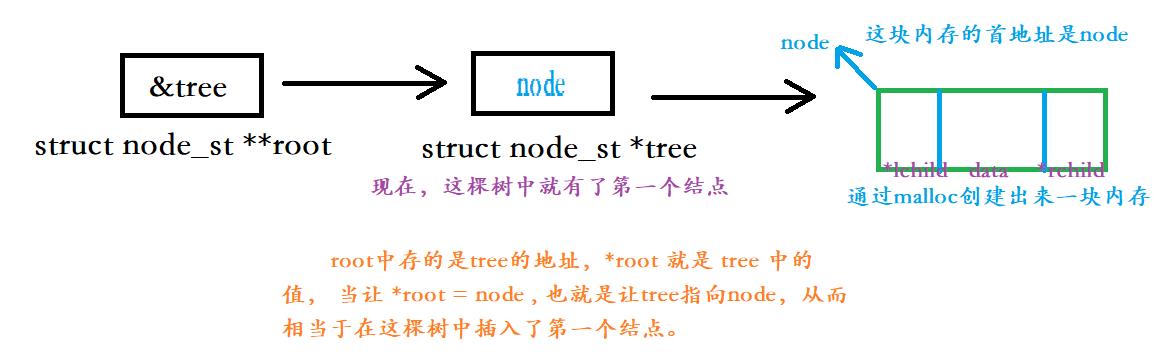 
这个程序实现了三个功能 1、在二叉树中插入结点 2、根据 id 来查找结点 3、采用 “左倒” 的方式将二叉树给绘制出来。
程序代码如下
目前对于递归的思想没有理解的很透彻
#include #include #define NAMESIZE 32struct score_st{int id;char name[NAMESIZE];int math;int chinese;};/*二叉链表的基本思想令二叉树的每个结点对应一个链表结点链表结点除了存放与数据信息之外还要设置指示左右孩子的指针。*///二叉链表的缺点--不能够通过孩子结点来找到它的双亲struct node_st{//数据域struct score_st data;//指针域struct node_st *lchild,*rchild;};//待插入的数据 -- 要遵循一定的原则//注意第一个参数是一个二级指针int insert(struct node_st **root,struct score_st *data){struct node_st *node;//当第一个结点插入进来if(*root NULL){node malloc(sizeof(*node));if(node NULL)return -1;node->data *data;node->lchild NULL;node->rchild NULL;*root node ;return 0;}//将要插入的这个结点的id与当前结点的id进行比较//如果相等或者更小的话就插入到左子树//否则就插入到右子树。if(data->id data.id)//.用于结构体变量访问成员,->用于结构体指针访问成员return insert(return insert(}void print_s(struct score_st *data){printf("%d %s %d %d.\n",data->id,data->name,data->math,data->chinese);}struct score_st *find(struct node_st *root,int id){if(root NULL)return NULL;if(id root->data.id)return if(id data.id)return find(root->lchild,id);elsereturn find(root->rchild,id);}//struct node_st *root -- 当前结点//level -- 当前结点所在的层数void draw_(struct node_st *root,int level){int i;//如果当前结点为叶子结点if(root NULL)return;//父结点的右子树 -- 右子树位于它的父结点的下一层draw_(root->rchild,level1);for(i0;idata);//左子树 -- 左子树位于它的父结点的下一层draw_(root->lchild,level1);}void draw(struct node_st *root){//画图采用向左倒的方式/* CA 左倒 // \ ---> AB C \B*/// 画出这样的一棵树需要有两个要素1、要分清楚当前结点的左右子树// 2、还要进行计数,得到当前数的度(层数),方便计算出空格数draw_(root,0);//从这棵树的第一层,即根节点开始}int main(){int i;int arr[] {1,2,3,7,6,5,9,8,4};//一说到链式存储,就要反应到要不要有头结点//这里,头结点没有什么必要。//创建一颗空树struct node_st *tree NULL;//我要想调用insert的话,首先把每个结点的数据结构给做出来struct score_st tmp,*find_result;//我们要使用insert函数将这棵树给构建起来for(i0;i < sizeof(arr)/sizeof(*arr);i){tmp.id arr[i];snprintf(tmp.name,NAMESIZE,"stu%d",arr[i]);tmp.math rand()%100;tmp.chinese rand()%100;//这棵数由于是不带头结点的,所以起始位置会变化,所以应该传入的是这棵树的地址过去.insert(}//把这棵树给绘制出来draw(tree);//这里将查找的测试代码给注释了#if 0//我要来查找有没有id为2的那个人int tmpid 2;//我希望在这棵树中查找一个指定的idfind_result find(tree,tmpid);if(find_result NULL)printf("Can not find the id %d . \n",tmpid);elseprint_s(find_result);return 0;#endif}
对于该程序的递归调用参考 https://www.bilibili.com/video/BV1ze411x7x8.