文章目录
- 前言
- 一、神经网络的全连接层
- 二、**函数
- 三，误差计算
- 四，梯度下降
- 五，反向传播
- 总结
前言
提示：这里可以添加本文要记录的大概内容： 例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。
提示：以下是本篇文章正文内容，下面案例可供参考
一、神经网络的全连接层
对于线性函数 h=relu([email protected]+b)的图形解释如下：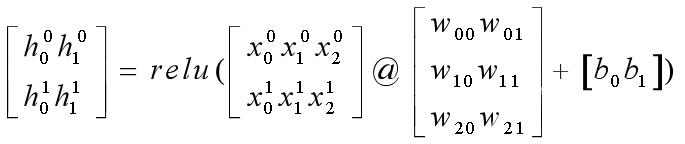
令输出h是一个两行两列的矩阵，输入X是一个两行三列的矩阵，权值W是一个三行两列的矩阵，偏置b为0，**函数为relu函数。当且仅当只看输入x0,x1,x2，则对应的模型部分的图形解释如图：
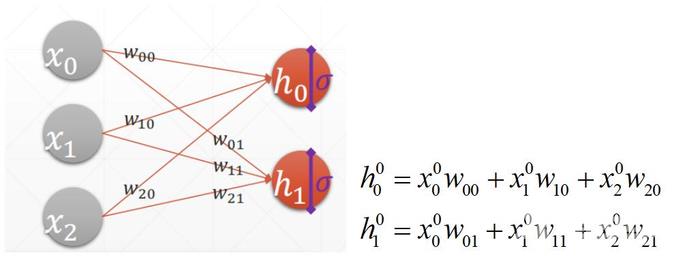完全符合矩阵运算，其输入需要经过relu函数进行判定，即公式 h=relu([email protected]+b) 在此基础上增加输入值数量和隐藏层h1,h2,h3…hn.即构成简单的多层神经网络结构的模型。如图所示：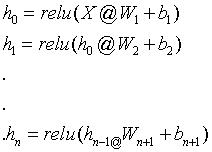
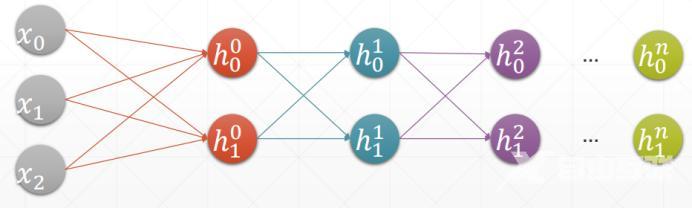
示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。
二、**函数
**函数是用来控制数据输出的，模拟生物的神经元则解释为**函数为细胞核，当给与细胞的刺激（输入）不同时，细胞做出的反应（输出）不同。通过**函数，可以让神经网络模型解决非线性问题，且一个合适的**函数可以让模型快速收敛，以得到合适的解。以下简单介绍三个广泛运用的**函数。
三，误差计算
前面已经讲解了神经网络的基本模型，那么对于模型的输出结果是如何进行衡量和优化的呢？这便是下面讲述的重点——损失（误差）函数loss 对于有监督神经网络来说，我们将模型的输出称为预测值，将被预测物体的事实称为真实值，预测值越逼近真实值，则模型越好，而衡量的标准称为loss。 以下给出常用的二种loss：MSE（mean square error） 分为两种，一种的平方差均值，另一种是2范数。 y是真实值（ground-truth） out为预测值（prob）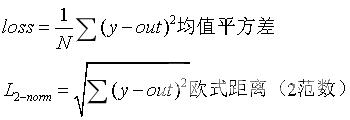
CEL（cross entropy loss）交叉熵 常用于分类问题。p,q为不同的事件。
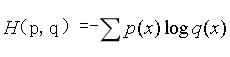熵的意义：一件事的熵越大，则该事件的惊喜度越低，该事件越稳定越确定。
总的来说，优化神经网络的过程就是让loss变小的过程，即不断更新loss的过程。
四，梯度下降
介绍了优化神经网络的标准，即loss。而优化loss最常见的方法便是梯度下降法。梯度是一个向量，是函数在每个方向的导数的组合。梯度的方向代表函数值增大的方向，梯度的长度代表函数增大的速度。所以，loss减少的过程就是函数向梯度减少的方向进行更新的过程。令loss为平方差均值，f(x)为线性感知机模型WX+b，即：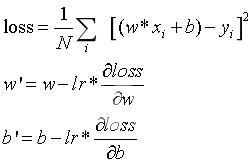
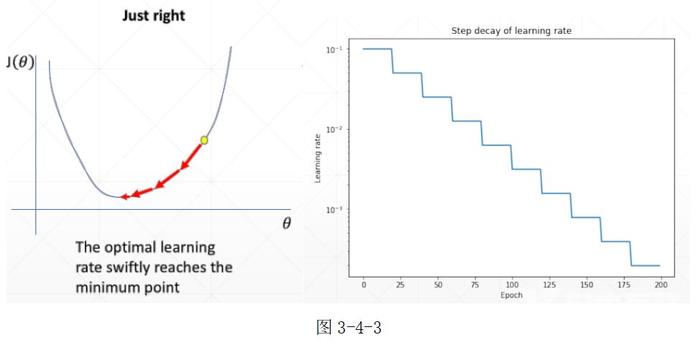
W’和b’分别向梯度相反的方向更新，目的是使W’* x + b’-> y，而使得loss变小。lr是学习步长（learning rate）通过lr控制更新的步长，lr的设置要合理，若过大则很容易产生梯度震荡而得不到最优解，而lr过小会导致训练速度过慢，训练不容易收敛。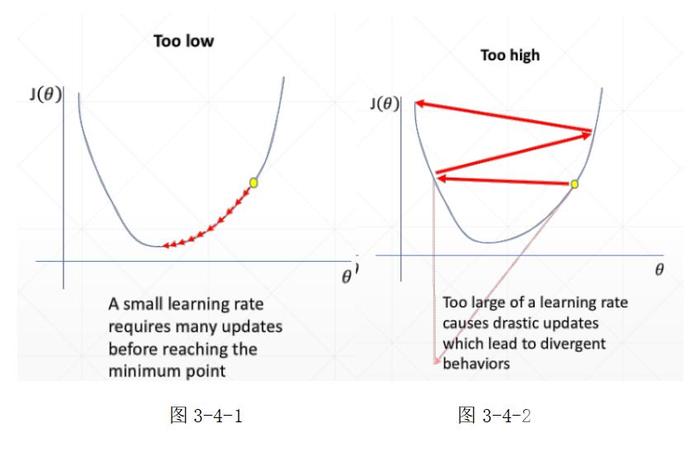
如图3-4-1所示，若参数lr过小，模型更新时每次向最小值的点移动的距离很小，模型的训练时间越长，且若loss函数复杂可能会造成梯度收敛困难。 如图3-4-2所示，若参数lr过大，模型更新时每次向最小值的点移动的距离很大，可能造成权值更新的来回震荡，而得不到最优解（最小值）。 设置lr的一个较好的方式是——learning rate decay。即刚因为起始点可能距离最优解较远，lr可以设置的较大（如0.01），随着模型更新次数的迭代，lr也逐渐减少，便于求得最优解，如图3-4-3所示。
五，反向传播
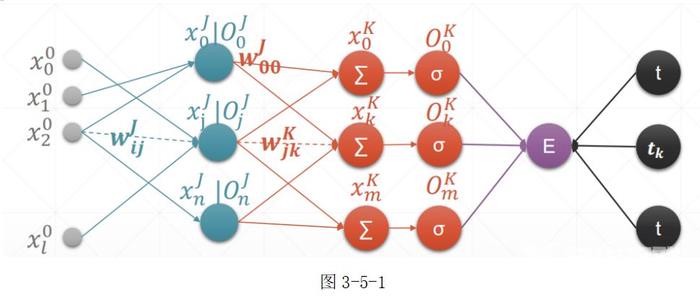
通过以上介绍我们已经建立了一个简单的神经网络模型，且探讨的如何求得最优解的方法，接下我们将探讨如何更新模型的权值，使模型得到自我优化。一个最经典的方法就是反向传播。
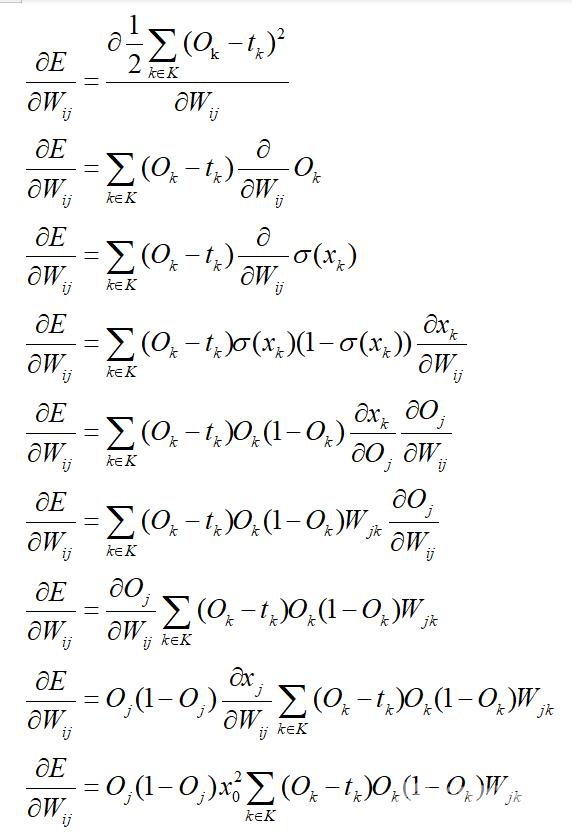
总结
本章依次讲解了神经网络模型的建立，**函数，误差分析，梯度下降和反向传播，这五部组合起来就是完整的BP神经网络模型