数字信号处理——IIR滤波器设计

一、前言。IIR滤波器是利用模拟滤波器经过变换得到数字滤波器。所以要先介绍模拟滤波器的设计。二、模拟滤波器设计。1.1巴特沃斯低通滤波器设计。巴特沃斯的模方函数如下close all;clc;As=10; %dBAp=1;ws=0.4 * pi; %rad/swp=0.1 * pi;N = order(As,Ap,ws,wp);fprintf(N = %d\r\n,N);[wc1,wc2] = cutFreq(As,Ap,ws,wp,N);fprintf(wc = [%0.4f , %0.4f]\r\n,wc1,wc2);syms s wcS = pole(N);Hs = sysFunc(S);pretty(expand(Hs)) % 计算系统函数wcc = wc1; %代入wc计算零极点分布图b = [wcc^2]; %系统函数分子a = [1 sqrt(2)*wcc wcc^2]; %系统函数分母sys = tf(b,a)subplot(211);pzmap(sys)w = 0:0.01:2*pi;wc = wc2;Gw = gainFunc(N,wc,w);subplot(212);plot(w,Gw); % 计算增益曲线图wsValue = gainFunc(N,wc,ws); %标记ws,wpwpValue = gainFunc(N,wc,wp);text(ws,wsValue,o,color,r)text(wp,wpValue,o,color,b)text(ws,-5,[(ws=,num2str(ws,%0.1f),,G=,num2str(wsValue,%0.1f),dB)],color,r)text(wp,-22,[(wp=,num2str(wp,%0.1f),,G=,num2str(wpValue,%0.1f),dB)],color,b)function N = order(As,Ap,ws,wp) % 计算阶数Nn = log10( (10^(0.1*As) - 1) / (10^(0.1*Ap) - 1) );m = 2*log10(ws/wp);N = ceil(n/m);function [wc1,wc2] = cutFreq(As,Ap,ws,wp,N) % 计算截止频率 wc1 <= wc <= wc2wc1 = wp / ((10^(0.1*Ap) - 1)^(1/(2*N)));wc2 = ws / ((10^(0.1*As) - 1)^(1/(2*N)));function S = pole(N) % 计算极点syms wcfor k=1:NS(k) = wc * exp(i*pi*(1/2 + (2*k-1)/(2*N) ));endfunction Hs = sysFunc(S) % 计算系统函数N = length(S);Hs = 1;syms s wcfor k=1:NHs = Hs * ( (-S(k)) / ( s - S(k) ));endfunction Gw = gainFunc(N,wc,w) % 增益函数 Gw=-AwGw = -10*log10(1 + ((w/wc) .^ (2*N)));

最终结果如下：

1.2 切比雪夫I型低通滤波器。

切比雪夫I型的模方函数如下：

设计步骤如下：

function [] = cb1_filter() %切比雪夫I型低通滤波器clear;close all;clc;As=10; %dBAp=1;ws=0.4 * pi; %rad/swp=0.1 * pi;wc=wp;epsilon = epsilonCalulate(Ap); % 计算epsilonN = order(As,epsilon,ws,wp); % 计算阶数Nfprintf(epsilon = %d\r\n,epsilon);fprintf(N = %d\r\n,N);fprintf(wc = %0.4f\r\n,wc);S = pole(N,epsilon) % 计算极点Hs = sysFunc(S,N,epsilon); % 计算系统函数digits(5); %减少小数位数pretty(expand(vpa(Hs,4))) % 化简系统函数b = [0.794]; %系统函数分子a = [1 1.1 1.1]; %系统函数分母sys = tf(b,a)subplot(211);pzmap(sys)w = 0:0.01:2*pi;Gw = gainFunc(N,wc,w,epsilon);subplot(212);plot(w,Gw); % 计算增益曲线图wsValue = gainFunc(N,wc,ws,epsilon); %标记ws,wpwpValue = gainFunc(N,wc,wp,epsilon);text(ws,wsValue,o,color,r)text(wp,wpValue,o,color,b)text(ws,1,[(ws=,num2str(ws,%0.1f),,G=,num2str(wsValue,%0.1f),dB)],color,r)text(wp,5,[(wp=,num2str(wp,%0.1f),,G=,num2str(wpValue,%0.1f),dB)],color,b)function N = order(As,epsilon,ws,wp) % 计算阶数Nn = acosh((1/epsilon)* sqrt( (10^0.1*As) - 1 ) );m = acosh(ws/wp);N = ceil(n/m);function epsilon = epsilonCalulate(Ap) % 计算epsilOnepsilon= sqrt((10 ^ (0.1*Ap)) - 1);function S = pole(N,epsilon) % 计算极点beta = asinh(1/epsilon) / N;for k=1:Nsita = -sinh(beta)*sin( (2*k-1)*pi/(2*N) );omiga = -cosh(beta)*cos( (2*k-1)*pi/(2*N) );S(k) = sita + i*omiga;endfunction h0 = h0Calulate(N,epsilon) % 计算H0if(mod(N,2) == 0) %偶数h0 = sqrt( 1/(1 + (epsilon^2)) );elseh0 = 1;endfunction Hs = sysFunc(S,N,epsilon) % 计算系统函数N = length(S);Hs = 1;h0 = h0Calulate(N,epsilon); % 计算H0syms sfor k=1:NHs = Hs * (h0 / ( s-S(k) ));endfunction CNx = cnxFunc(N,x) % 计算CN(x)函数for i=1:length(x)if abs(x(i)) <= 1CNx(i) = cos(N*acos(x(i)));elseCNx(i) = cosh(N*acosh(x(i)));endendfunction Gw = gainFunc(N,wc,w,epsilon) % 增益函数 Gw=-AwGw = -10*log10(1 + (epsilon^2) * cnxFunc(N,w/wc) );

最终结果如下：

1.3 切比雪夫II型低通滤波器。

切比雪夫II型的模方函数如下：

设计步骤如下：

function [] = cb2_filter() %切比雪夫II型低通滤波器clear;close all;clc;As=10; %dBAp=1;ws=0.4 * pi; %rad/swp=0.1 * pi;wc=ws;epsilon = epsilonCalulate(As); % 计算epsilonN = order(Ap,epsilon,ws,wp); % 计算阶数Nfprintf(epsilon = %d\r\n,epsilon);fprintf(N = %d\r\n,N);fprintf(wc = %0.4f\r\n,wc);S = pole(N,epsilon) % 计算极点Hs = sysFunc(S,N,epsilon); % 计算系统函数digits(4); %减少小数位数pretty(expand(vpa(Hs,2))) % 化简系统函数b = [1]; %系统函数分子a = [1 1.47 1.581]; %系统函数分母sys = tf(b,a)subplot(211);pzmap(sys)w = 0.01:0.01:2*pi;Gw = gainFunc(N,wc,w,epsilon);subplot(212);plot(w,Gw); % 计算增益曲线图wsValue = gainFunc(N,wc,ws,epsilon); %标记ws,wpwpValue = gainFunc(N,wc,wp,epsilon);text(ws,wsValue,o,color,r)text(wp,wpValue,o,color,b)text(ws,-20,[(ws=,num2str(ws,%0.1f),,G=,num2str(wsValue,%0.1f),dB)],color,r)text(wp,-3,[(wp=,num2str(wp,%0.1f),,G=,num2str(wpValue,%0.1f),dB)],color,b)function N = order(Ap,epsilon,ws,wp) % 计算阶数Nn = acosh(1/(epsilon * sqrt( (10^(0.1*Ap)) - 1 ) ));m = acosh(ws/wp);N = ceil(n/m);function epsilon = epsilonCalulate(As) % 计算epsilOnepsilon= 1/(sqrt((10 ^ (0.1*As)) - 1));function S = pole(N,epsilon) % 计算极点beta = asinh(1/epsilon) / N;for k=1:Nsita = -sinh(beta)*sin( (2*k-1)*pi/(2*N) );omiga = -cosh(beta)*cos( (2*k-1)*pi/(2*N) );S(k) = sita + i*omiga;endfunction Hs = sysFunc(S,N,epsilon) % 计算系统函数N = length(S);Hs = 1;h0 = 1; % wc>0 endfunction CNx = cnxFunc(N,x) % 计算CN(x)函数for i=1:length(x)if abs(x(i)) <= 1CNx(i) = cos(N*acos(x(i)));elseCNx(i) = cosh(N*acosh(x(i)));endendfunction Gw = gainFunc(N,wc,w,epsilon) % 增益函数 Gw=-Awn = (epsilon^2) * (cnxFunc(N,wc./w).^2);m = 1+n;Gw = 10*log10(n./m);

最终结果如下：

1.4 椭圆低通滤波器。

由于没有找到合适的资料，这里略。

三、模拟域频率转换。

要想设计模拟高通、带通、带阻滤波器，先设计低通滤波器，再经过频率转换后，得到其它滤波器。

2.1 低通到高通。

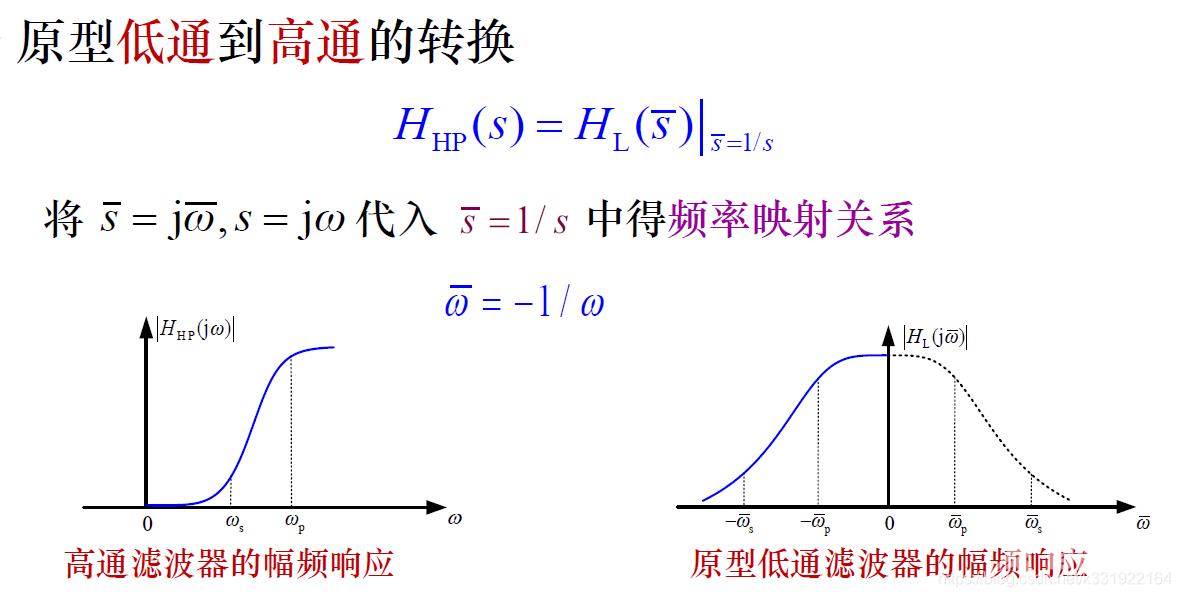
2.2 低通到带通。

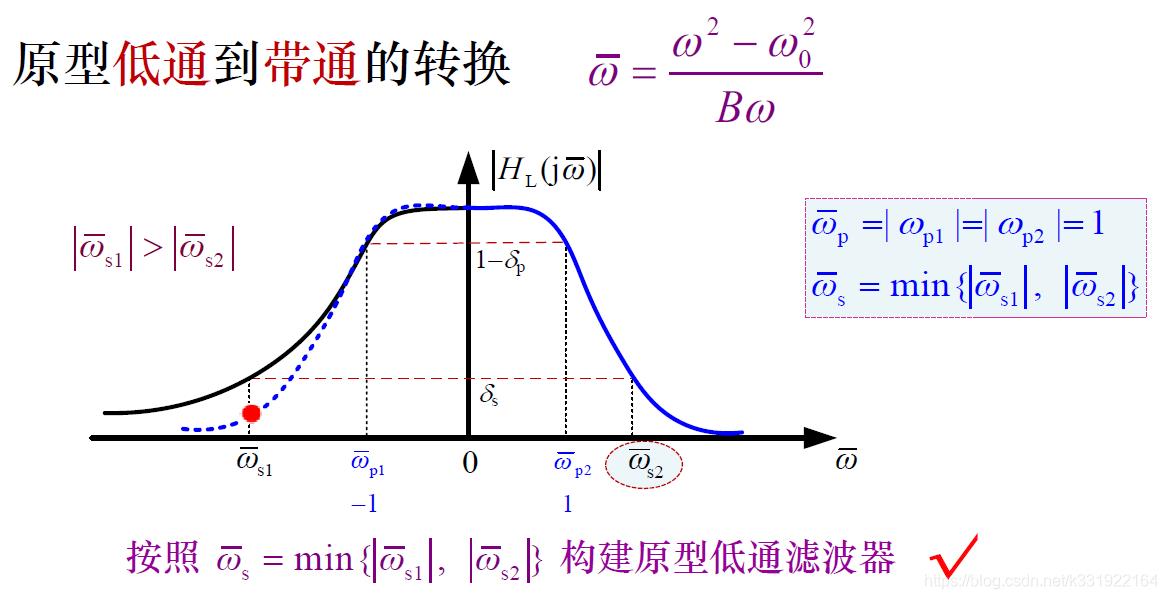
2.3 低通到带阻。

2.4 总结。

先用高通、带通、带阻的参数指标，经过频率转换，得到低通的参数指标，再设计好低通滤波器得到低通的系统函数H(s)，

最后通过复频率转换，得到高通、带通、带阻的系统函数。其中频率转换的代码如下：

function [] = freq_conv() %模拟频率转换clear;close all;clc;wp1 = 10; wp2 = 30; ws1 = 19; ws2 = 21;[lpws,lpwp] = bs2lp(ws1,ws2,wp1,wp2)wp1 = 6; wp2 = 8; ws1 = 4; ws2 = 11;[lpws,lpwp] = bp2lp(ws1,ws2,wp1,wp2)function [lpws,lpwp] = hp2lp(hpws,hpwp) % 高通到低通lpws = 1/hpws;lpwp = 1/hpwp;function [lpws,lpwp] = bp2lp(bpws1,bpws2,bpwp1,bpwp2) % 低通到带通B = abs( bpwp2 - bpwp1 );w0_2 = bpwp1 * bpwp2;ws1_ = (bpws1^2 - w0_2) / (B * bpws1);ws2_ = (bpws2^2 - w0_2) / (B * bpws2);lpws = min(abs(ws1_),abs(ws2_));lpwp = 1;function [lpws,lpwp] = bs2lp(bsws1,bsws2,bswp1,bswp2) % 带阻到低通B = abs( bsws2 - bsws1 );w0_2 = bsws1 * bsws2;wp1_ = (B * bswp1) / (-(bswp1^2) + w0_2) ;wp2_ = (B * bswp2) / (-(bswp2^2) + w0_2) ;lpwp = max(abs(wp1_),abs(wp2_));lpws = 1;

四、脉冲响应不变法。

脉冲响应不变法的原理是：得到模拟滤波器的系统函数H(s)，经过拉氏反变换得到时域的h(t)，通过抽样到得离散的h(t)，再经过z变换得到数字滤波器的H(z)。

由于这里用到时域抽样，所以一定要保证h(t)为带限信号，所以脉冲响应不变法不能用于设计高通、带阻（存在高频分量、非带限）滤波器。

五、双线性变换法。

双线性变换法的原理是在脉冲响应不变法的基础上，进行改进。

通过arctan/tan函数将非带限信号转换为带限信号（arctan、tan的等价无穷小为x），也就是说在x很小时候，可以看作是线性变换。

再设计出模拟滤波器得到系统函数H(s)，再经过第二次线性变换，得到H(z)。

由于双线性变换可以将非带限信号转为带限信号，那么它可以设计高通、低通、带通、带阻滤波器。