【转】基础算法转载声明
本文是基础极其薄弱的博主根据OI-Wiki上的相关内容组织而成,自己写的东西很少,大部分摘自上述的学习网站,摘选的内容也是博主自己掌握不好或者没写过笔记的知识点,特此声明。 狗头保命??
话说那个网站真的好,语言简练又不失重点,如果担心博主我写的可能不准确,可以参看那个网站上的相关内容,标题是相同的。
递归和分治
他讲的很详细,很好,我就不复制粘贴了....强烈推荐去看看
贪心
贪心算法顾名思义就是用计算机来模拟一个“贪心”的人做出决策的过程。
这个人每一步行动总是按某种指标选取最优的操作,他总是 只看眼前,并不考虑以后可能造成的影响 。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
常见做法
在提高组难度以下的题目中,最常见的贪心有两种。
- 一种是:「我们将 XXX 按照某某顺序排序,然后按某种顺序(例如从小到大)处理」。
- 另一种是:「我们每次都取 XXX 中最大/小的东西,并更新 XXX」,有时「XXX 中最大/小的东西」可以优化,比如用优先队列维护。
为啥分成两种?你可以发现,一种是离线的,一种是在线的。
证明方法
从来都是大胆猜想,从来不会小心求证
以下套路请按照题目自行斟酌,一般情况下一道题只会用到其中的一种方法来证明。
排序法
用排序法常见的情况是输入一个包含几个(一般一到两个)权值的数组,通过排序然后遍历模拟计算的方法求出最优值。
有些题的排序方法非常显然,如 「USACO1.3」修理牛棚 Barn Repair 就是将输入数组差分后排序模拟求值。
然而有些时候很难直接一下子看出排序方法,比如 NOIP 2012 国王游戏, 一个常见办法就是尝试交换数组相邻的两个元素来 推导 出正确的排序方法。
证明方法详见原网址
如果看懂了就可以尝试下一道类似的题: Luogu P2123 皇后游戏
看了两个小时,然后发现这题并不是那么简单。。。。这里贴上luogu题解,建议观摩前三篇题解(尤其是第三篇),博主实力有限,就不献丑了...本来这题准备直接粘贴代码的,现在copy都不敢了2333
就只写一个注意点吧:
在结构体里重载运算符<时,不能在里面写=之类的
因为重载过后,它判定相等的方式是:!(a=b),当a, b真的相等的时候,是不会判定正确的。
而写之类的就行,因为它判相等的方式和上面的一样:!(ab),所以是合法的....吧(我口胡的
我发现这种用排序法做贪心的题型,按题意写出不等关系后,需要做的就是把引入的参数想办法消掉,之后只得出用相邻两个struct所含的元素组成的不等式,然后编写排序函数求解。
后悔法
「USACO09OPEN」工作调度 Work Scheduling
贪心思想:
按照时间顺序,每一项工作都做,遇见时间不够的现象,就在之前的时间中选出利润最小的工作,与当前工作做比较,如果当前工作利润更高,就“回到过去”,不做那个工作,即后悔,然后做这个工作。
排序
归并排序
采用分治思想
//左闭右开void merge(int ll, int rr) { if(rr - ll <= 1) return ; int mid = ll + ((rr - ll) >> 1); merge(ll, mid); merge(mid, rr); int p = ll, q = mid, s = ll; while(s <= rr) { if(p >= mid || (q a[q])) { tmp[s++] = a[q++]; //ans += (long long)mid-p; }else tmp[s++] = a[p++]; } for(int i = ll; i 原网址,有需要的同学请进 这里只补充我没学过的,全部详细内容请进 int l = 1, r = 1000000001; //因为是左闭右开的,所以右边界要加1 while (l + 1 (求合法的最大值的题目提问的形式大多是:“求最大的XXX”或者“再大一点就不成立”或者其他的什么,总之要好好读题,因为这不是绝对的,因题而异): 因为搜到最后,会这样 然后会: 合法的最小值恰恰相反。 倍增,从字面上理解就是加倍增加,是一种思想。 和二进制联系较为紧密,通常运用是RMQ和求LCA。 给出一个长度为\(n\) 的环和一个常数 \(k\),每次会从第 \(i\) 个点跳到第\((i+k) \mod n + 1\)个点,总共跳了\(m\)次。每个点都有一个权值,记为$ a_i\(,求\)m$次跳跃的起点的权值之和对\(10^9 +7\) 取模的结果。 数据范围:$ 1 \le n \le 10^6, 1 \le m \le 10^{18}, 1 \le k \le n, 0 \le a_i \le 10^9$ 分析:每个数都可以表示成二进制的形式,所以我们显然不用(也显然不能)直接枚举, 对于从每个点开始的\(2^i\)步,记录一个 go[i][x] 表示第\(x\) 个点跳\(2^i\)步之后的终点,而 sum[i][x] 表示点权和。对于跳\(2^i\)步的信息,预处理的时候可以看作是先跳了\(2^{i-1}\),再跳了\(2^{i-1}\)步。 总结: 这就是倍增预处理出以二的整数次幂为单位的信息: 在递推中,如果状态空间很大,可以通过成倍增长的方式,只递推出状态空间在2的整数次幂的值作为代表。 要求这个递推问题的状态空间关于2的次幂具有可划分性。 注意:为了保证统计的时候不重不漏,一般预处理出左闭右开的点权和。 还有个应用,就是ST表 原题链接, 大意如下(因为我是看的大意,所以就不写原题了): 给定一个整数 ??,对于任意一个整数集合 ??,定义“校验值”如下:从集合 ?? 中取出 ?? 对数(即 2×?? 个数,不能重复使用集合中的数,如果 ?? 中的整数不够 ?? 对,则取到不能取为止),使得“每对数的差的平方”之和最大,这个最大值就称为集合 ?? 的“校验值”。 现在给定一个长度为 ?? 的数列 ?? 以及一个整数 ??。我们要把 ?? 分成若干段,使得每一段的“校验值”都不超过 ??(貌似原来的顺序不能被改变)。求最少需要分成几段。 多测,测试组数为 T\[T \leq 12,1 \leq n, m \leq 5 \times 10^{5}, 0 \leq k \leq 10^{18}, 0 \leq P_i\leq 2^{20}\]分析: 先考虑怎么对每一段求“校验值”:把每一段的最大的M个和最小的M个配对,最大配最小,所得结果即为校验值(可以用四个数自己证明一下)。 题目说要是的分的段数最少,所以每一段都应该尽量在合法的条件下,包含更多的数。这时问题变为:当确定左端点L时,右端点在合法时,最大能取到哪。这就变成了找区间长度的问题。 当校验值较小时,在整段区间上二分右端点R是有点不划算的(二分从中间判断,但是最后R可能只扩展了1点); 总结:需要与右端点R扩展的长度相适应的算法:倍增。 以下代码最后一个点T掉了... #include#includeusing namespace std;#pragma GCC optimize(3,"Ofast","inline")const int N = 5e5+9;inline int read() { int x = 0; char ch = getchar(); while(ch9) {ch = getchar();} while(ch>=0 9) {x = (x<<3)+(x<<1)+(ch^48); ch = getchar();} return x;}int p[N], n, m, T, kl, kr, tmp[N], a[N];//kl, kr 保存上一次调整区间的l,rlong long K;void merge(int l, int r, int x, int y) {//只是把俩有序序列合并 int i = l, j = x, s = l; while(s <= y) { if(i > r || (j a[j])) tmp[s++] = a[j++]; else tmp[s++] = a[i++]; } for(int i = l; i <= y; i++) a[i] = tmp[i];}bool judge(int l, int r) { if(l == kl i <= r; i++) a[i] = p[i]; sort(a+kr+1, a+r+1);//只需先把[kr+1, r]弄有序 merge(kl, kr, kr+1, r);//再merge这俩区间就行了(如果一直sort会超时) kr = r;//记得更新 }else {//说明此时已换另一段序列(有另一个左端点) kl = l, kr = r; for(int i = l; i <= r; i++) a[i] = p[i]; sort(a+l, a+r+1); } int k = 0; long long cnt = 0; while(k 因为主要是讲解题目,所以有需要的同学请点这里这里 摘选内容不完整,简直寻章摘句,所以,对于想要打好基础的同学,务必前往原地址学习 再次感谢。
快速排序
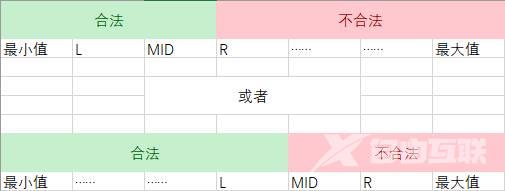
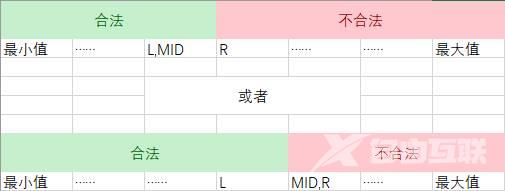
二分
倍增
例题:认识倍增
例题:倍增与二分
构造
后记
