研究生课程系列文章参见索引《在信科的那些课》题目一个旅行者准备随身携带一个背包可以放入背包的物品有n种每种物品的重量和价值分别为wj,vj.如果背 研究生课程系列文章参见索引
研究生课程系列文章参见索引《在信科的那些课》
题目
一个旅行者准备随身携带一个背包可以放入背包的物品有n种每种物品的重量和价值分别为wj, vj . 如果背包的最大重量限制是b, 怎样选择放入背包的物品以使得背包的价值最大? 目标函数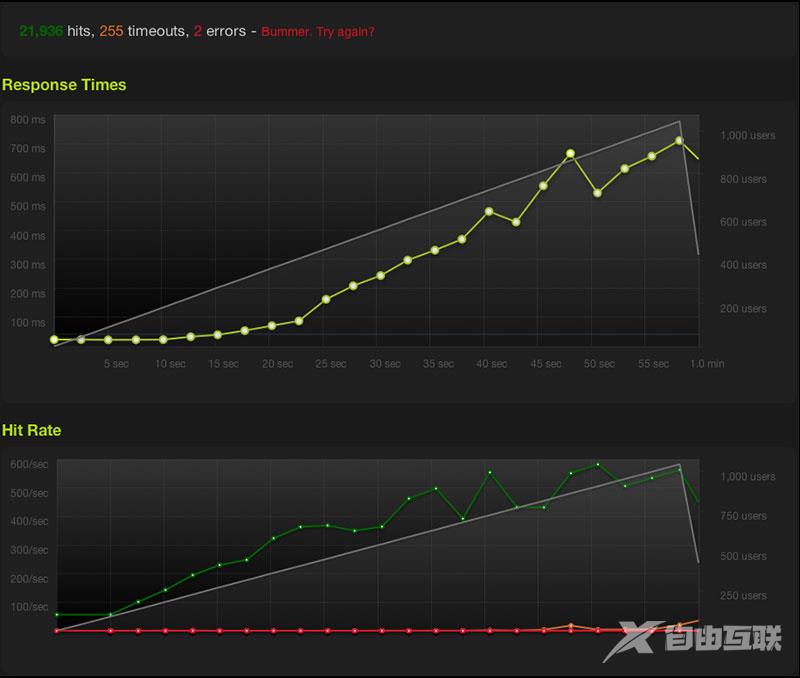
约束条件 
算法设计
设Fk(y) 表示只允许装前k 种物品,背包总重不超过y 时背包的最大价值。Fk(y)有两种情况不装第k件物品或至少装1件第k种物品。 如果不装第k件物品那么只能用前k-1件物品装入背包背包的限制重量仍为y所以最大价值是Fk-1(y) 如果装1件第k件物品那么装入的第k件物品价值为vk重量为wk剩下的物品仍要在前k件里选择因为每件物品可以装多件如果只能装1件就是在前k-1件里选择。于是问题规约为背包限制重量y-wk的情况下前k件物品取得最大价值即Fk(y-wk)vk。递推方程与边界条件
上式初值比较多F0(y)是不装物品的最大价值F1(y)是只能装第一件物品时最多装|_y/w1_|件递推式Fk(y-wk)y-wk有可能得到负值即不能再装物品所以设置最小数以保证在优化问题中淘汰这种情况。 算法实现
标记函数实现是需要一个ik(y)记录优化函数Fk(y)用到物品的最大标号。计算Fk(y)时如果Fk-1(y)>Fk(y-wk)vk即没有加入第k件物品ik(y)即为Fk-1(y)的物品最大标号反正加入第k件物品ik(y)记为k。标记函数递归关系
代码如下 void Knapsack(int v[N],int w[N],int F[][B1],int tagi[][B1]){for(int k0;k
实例及解的追踪
试验下面的例子 v11v23v35v49w12w23w34w47b10 运行结果如下图
我们需要在标记函数ik(y)中把实际解及每个物品分别装入多少件追踪出来。 由最后i4(10)开始i4(10)4表示此时第4件物品至少装入1件占用重量w47于是背包剩余重量为10-73继续查询i4(3)由i4(3)2表示剩余物品最大标号为2第2件物品至少装入1件。剩余重量为0即不能再装入物品。用公式表示追踪解的过程 
根据实例可以理出追踪解的思路代码如下 void TrackSolution(int v[N],int w[N],int tagi[][B1]){//x[i-1]标记第i件物品的件数int x[N];for(int i0;i
其他题目
背包问题是很经典的动态规划问题很多问题都是背包的变种比如下面两个题目- 设P是一台Internet上的Web服务器。T{1,2,...,n}是n个下载请求集合ai为正整数表示下载请求i所申请的带宽已知服务器的最大带宽是正整数K。我们的目标是使带宽得到最大限度的利用即确定T的一个子集S使得
且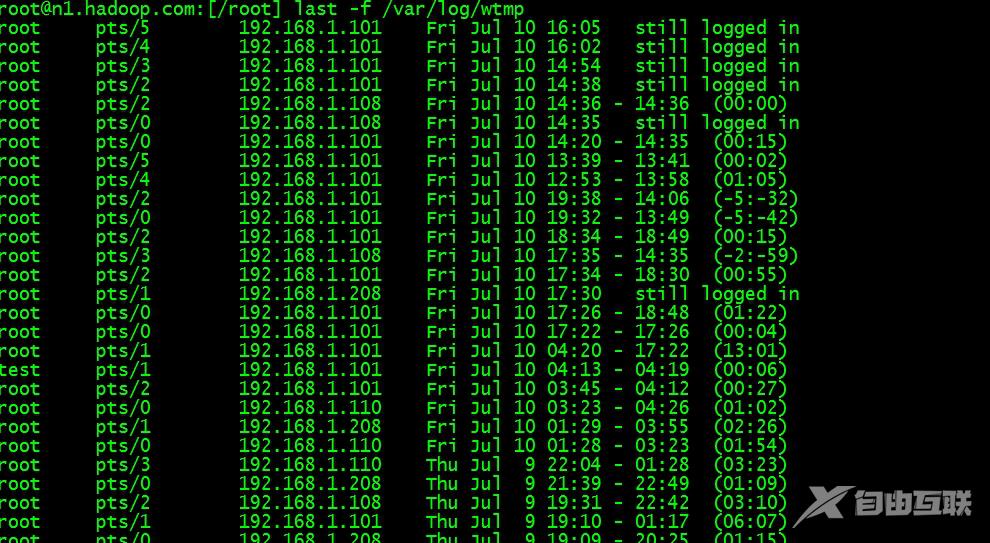
达到最小。设计一个算法求服务器下载问题。 - 设有n项任务加工时间分别表示为正整数t1t2...tn。现有2台同样的机器从0时刻可以安排对这些任务的加工知道T时刻所有任务完成总加工时间为T。设计算法使得总加工时间T最小的调度方案。
注意0-1背包和背包问题的递推关系主要区别是当选择第k件物品时Fk(y)表示为Fk-1(y-wk)vk而非Fk(y-wk)vk即只能在前k-1件物品里继续选择。另外F1(y)的边界函数也不同。 至于第二个题目其实就是使得一条加工线上的加工时间不超过T/2时加工时间尽可能大的问题和第一个问题是一样的。 代码下载http://download.csdn.net/detail/xiaowei_cqu/4775367 参考资料屈婉玲 刘田等 《算法设计与分析》