标签
二叉树、递归
题目
有一棵有\mathit nn个节点的二叉树其根节点为\mathit rootroot。修剪规则如下: 1.修剪掉当前二叉树的叶子节点但是不能直接删除叶子节点 2.只能修剪叶子节点的父节点修剪了父节点之后叶子节点也会对应删掉 3.如果想在留下尽可能多的节点前提下修剪掉所有的叶子节点。请你返回修剪后的二叉树。 有如下二叉树:
o/ \o o/ \ / \o o o o
修剪过后仅会留下根节点。
示例1
输入{1,1,1,1,1,1,1} 返回值{1}
说明叶子节点为最下面的4个1节点但是不能直接修剪只能修剪中间的2个1修剪掉之后只有根节点了 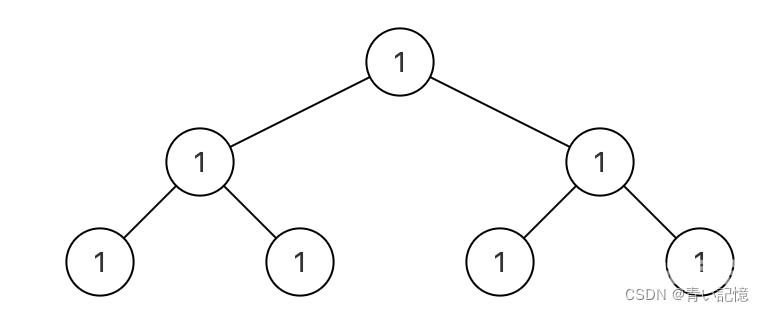
示例2
输入{1,#,1,#,1,#,1,#,1} 返回值{1,#,1,#,1}
说明退化为一条链了将最后两个节点删除。
反思
这道题目其实不难主要是要知道叶子节点怎么判断就行然后判断到叶子节点直接把叶子节点的父节点的通路给置为null
叶子节点的判断 node.left null null
用到的知识点
树、递归
代码
public class PruneLeaves {public TreeNode pruneLeaves(TreeNode root) {// write code hereif (root null) {return null;}if (root.left ! null) {if (root.left.left null null) {return null;} else {root.left pruneLeaves(root.left);}}if (root.right ! null) {if (root.right.left null null) {return null;} else {root.right pruneLeaves(root.right);}}return root;}}
