图是一种抽象数据结构,本质和树结构是一样的。
图与树相比较,图具有封闭性,可以把树结构看成是图结构的前生。如果将兄弟节点或子节点之间的水平连接应用于树形结构,则可以创建一个图形结构。
树适合描述从上向下的一对多的数据结构,如公司的组织结构。
图适合描述更复杂的多对多数据结构,如复杂的群体社交关系。
借助计算机解决现实世界中的问题时,除了要存储现实世界中的信息,还需要正确地描述信息之间的关系。
如在开发地图程序时,需要在计算机中正确模拟出城市与城市、或城市中各道路之间的关系图。只有在这个基础上,才能用算法计算出从一个城市到另一个城市,或从指定起点到目标点的最佳路径。
类似的还有航班路线图、火车线路图、社交交系图。
图结构可以有效地反映现实世界中如上所述信息之间的复杂关系。以此可使用算法方便的计算出如航班线路中的最短路径、如火车线路中的最佳中转方案,如社交圈中谁与谁关系最好、婚姻网中谁与谁最般配……
1.1 图的概念顶点:顶点也称为节点,可认为图就是顶点组成的集合。顶点本身是有数据含义的,所以顶点都会带有附加信息,称作"有效载荷"。
顶点可以是现实世界中的城市、地名、站名、人……
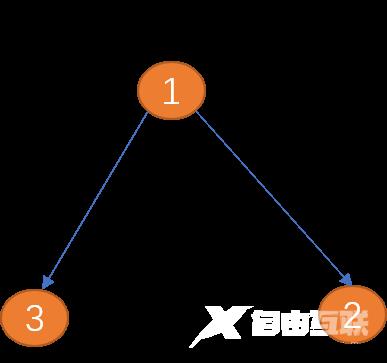
边: 图中的边用来描述顶点之间的关系。边可以有方向也可以没有方向,有方向的边又可分为单向边和双向边。
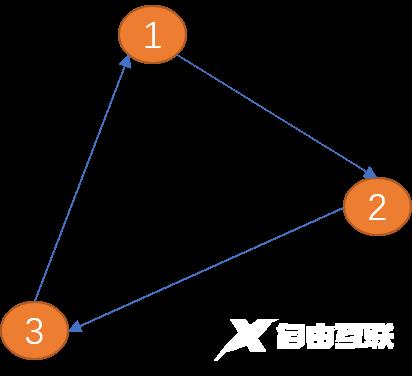
如下图(项点1)到(顶点2)之间的边只有一方向(箭头所示为方向),称为单向边。类似现实世界中的单向道。
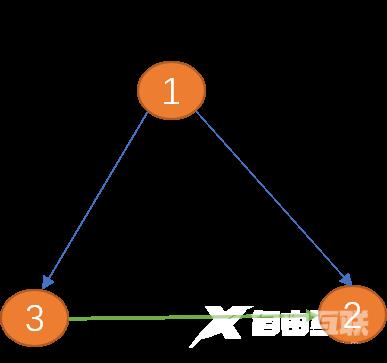
(顶点1)到(顶点2)之间的边有两个方向(双向箭头),称为双向边。 城市与城市之间的关系为双向边。
权重: 边上可以附加值信息,附加的值称为权重。有权重的边用来描述一个顶点到另一个顶点的连接强度。
如现实生活中的地铁路线中,权重可以描述两个车站之间时间长度、公里数、票价……
边描述的是顶点之间的关系,权重描述的是连接的差异性。
路径:
先了解现实世界中路径概念
如:从一个城市开车去另一个城市,就需要先确定好路径。也就是 从出发地到目的地要经过那些城市?要走多少里程?
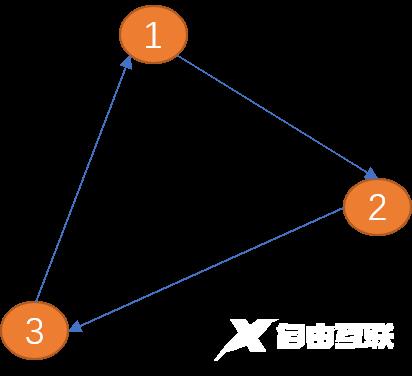
可以说路径是由边连接的顶点组成的序列。因路径不只一条,所以,从一个项点到另一个项点的路径描述也不指一种。
在图结构中如何计算路径?
无权重路径的长度是路径上的边数。
有权重路径的长度是路径上的边的权重之和。
如上图从(顶点1)到(顶点3)的路径长度为 8。
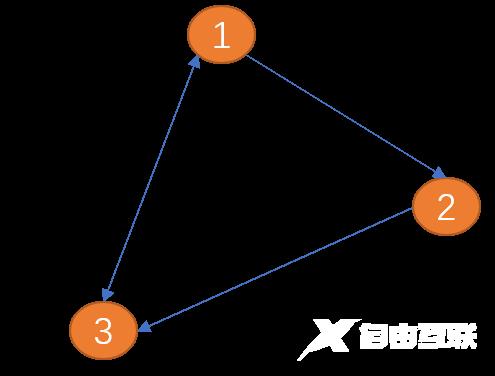
环: 从起点出发,最后又回到起点(终点也是起点)就会形成一个环,环是一种特殊的路径。如上 (V1, V2, V3, V1) 就是一个环。
图的类型:
综上所述,图可以分为如下几类:
有向图: 边有方向的图称为有向图。
无向图: 边没有方向的图称为无向图。
加权图: 边上面有权重信息的图称为加权图。
无环图: 没有环的图被称为无环图。
有向无环图: 没有环的有向图,简称 DAG。
根据图的特性,图数据结构中至少要包含两类信息:
所有顶点构成集合信息,这里用 V 表示(如地图程序中,所有城市构在顶点集合)。
所有边构成集合信息,这里用 E 表示(城市与城市之间的关系描述)。
如何描述边?
边用来表示项点之间的关系。所以一条边可以包括 3 个元数据(起点,终点,权重)。当然,权重是可以省略的,但一般研究图时,都是指的加权图。
如果用 G 表示图,则 G = (V, E)。每一条边可以用二元组 (fv, ev) 也可以使用 三元组 (fv,ev,w) 描述。
fv 表示起点,ev 表示终点。且 fv,ev 数据必须引用于 V 集合。
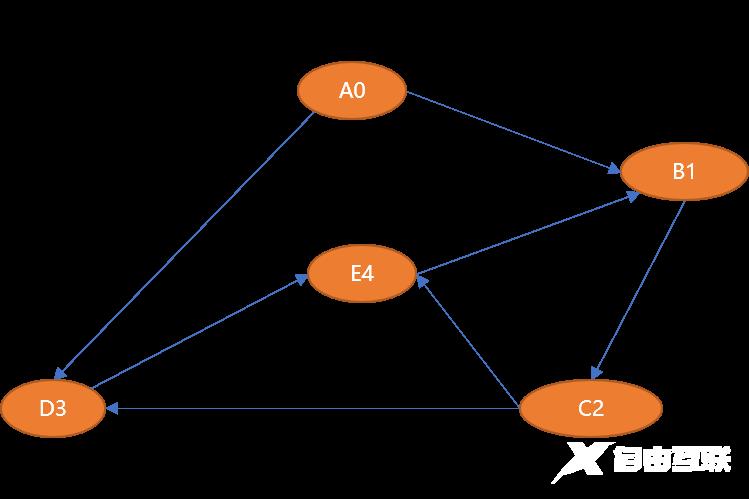
如上的图结构可以描述如下:
# 5 个顶点
V={A0,B1,C2,D3,E4}
# 7 条边
E={ (A0,B1,3),(B1,C2,4),(C2,D3,6),(C2,E4,1),(D3,E4,2),(A0,D3,5),(E4,B1,7)}1.3 图的抽象数据结构图的抽象数据描述中至少要有的方法:
Graph ( ): 用来创建一个新图。add_vertex( vert ):向图中添加一个新节点,参数应该是一个节点类型的对象。add_edge(fv,tv ):在 2 个项点之间建立起边关系。add_edge(fv,tv,w ):在 2 个项点之间建立起一条边并指定连接权重。find_vertex( key ): 根据关键字 key 在图中查找顶点。find_vertexs( ):查询所有顶点信息。find_path( fv,tv):查找.从一个顶点到另一个顶点之间的路径。
图的存储实现主流有 2 种:邻接矩阵和链接表,本文主要介绍邻接矩阵。
2.1 邻接矩阵使用二维矩阵(数组)存储顶点之间的关系。
如 graph[5][5] 可以存储 5 个顶点的关系数据,行号和列号表示顶点,第 v 行的第 w 列交叉的单元格中的值表示从顶点 v 到顶点 w 的边的权重,如 grap[2][3]=6 表示 C2 顶点和 D3 顶点的有连接(相邻),权重为 6
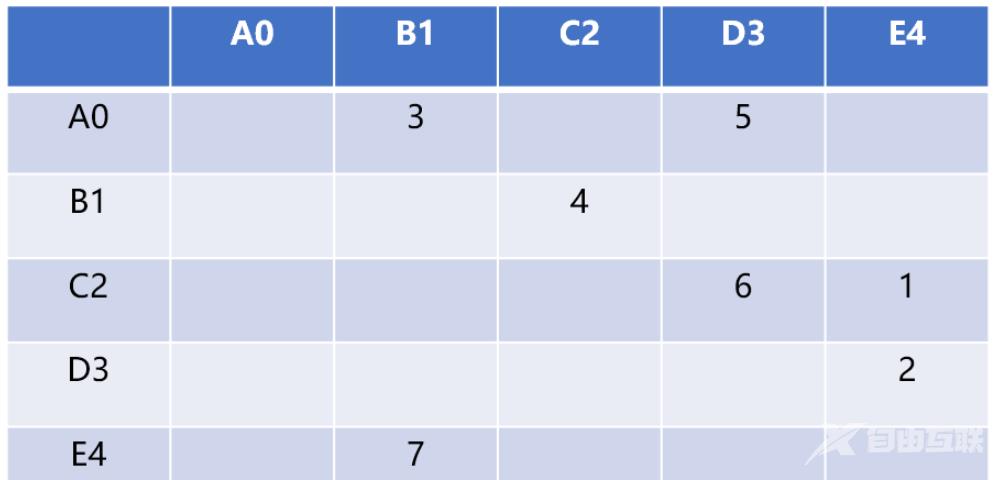
相邻矩阵的优点就是简单,可以清晰表示那些顶点是相连的。由于并非每对顶点之间都存在连接,因此矩阵中存在许多未被利用的空间,通常被称为“稀疏矩阵”。
只有当每一个顶点和其它顶点都有关系时,矩阵才会填满。如果图结构的关系不是太复杂,使用这种结构存储图数据会浪费大量的空间。
邻接矩阵适合表示关系复杂的图结构,如互联网上网页之间的链接、社交圈中人与人之间的社会关系……
2.2 编码实现邻接矩阵因顶点本身有数据含义,需要先定义顶点类型。
顶点类:
"""
节(顶)点类
"""
class Vertex:
def __init__(self, name, v_id=0):
# 顶点的编号
self.v_id = v_id
# 顶点的名称
self.v_name = name
# 是否被访问过:False 没有 True:有
self.visited = False
# 自我显示
def __str__(self):
return '[编号为 {0},名称为 {1} ] 的顶点'.format(self.v_id, self.v_name)顶点类中 v_id 和 v_name 很好理解。为什么要添加一个 visited?
这个变量用来记录顶点在路径搜索过程中是否已经被搜索过,避免重复搜索计算。
图类:图类的方法较多,这里逐方法介绍。
初始化方法
class Graph:
"""
nums:相邻矩阵的大小
"""
def __init__(self, nums):
# 一维列表,保存节点,最多只能有 nums 个节点
self.vert_list = []
# 二维列表,存储顶点及顶点间的关系(权重)
# 初始权重为 0 ,表示节点与节点之间还没有建立起关系
self.matrix = [[0] * nums for _ in range(nums)]
# 顶点个数
self.v_nums = 0
# 使用队列模拟队列或栈,用于广度、深度优先搜索算法
self.queue_stack = []
# 保存搜索到的路径
self.searchPath = []
# 暂省略……初始化方法用来初始化图中的数据类型:
一维列表 vert_list 保存所有顶点数据。
二维列表 matrix 保存顶点与顶点之间的关系数据。
queue_stack 使用列表模拟队列或栈,用于后续的广度搜索和深度搜索。
怎么使用列表模拟队列或栈?
列表有 append()、pop() 2 个很价值的方法。
append() 用来向列表中添加数据,且每次都是从列表最后面添加。
pop() 默认从列表最后面删除且弹出数据, pop(参数) 可以提供索引值用来从指定位置删除且弹出数据。
使用 append() 和 pop() 方法就能模拟栈,从同一个地方进出数据。
使用 append() 和 pop(0) 方法就能模拟队列,从后面添加数据,从最前面获取数据
searchPath : 用来保存使用广度或深度优先路径搜索中的结果。
添加新节(顶)点方法:
"""
添加新顶点
"""
def add_vertex(self, vert):
if vert in self.vert_list:
# 已经存在
return
if self.v_nums >= len(self.matrix):
# 超过相邻矩阵所能存储的节点上限
return
# 顶点的编号内部生成
vert.v_id = self.v_nums
self.vert_list.append(vert)
# 数量增一
self.v_nums += 1上述方法注意一点,节点的编号由图内部逻辑提供,便于节点编号顺序的统一。
添加边方法
此方法是邻接矩阵表示法的核心逻辑。
'''
添加节点与节点之间的边,
如果是无权重图,统一设定为 1
'''
def add_edge(self, from_v, to_v):
# 如果节点不存在
if from_v not in self.vert_list:
self.add_vertex(from_v)
if to_v not in self.vert_list:
self.add_vertex(to_v)
# from_v 节点的编号为行号,to_v 节点的编号为列号
self.matrix[from_v.v_id][to_v.v_id] = 1
'''
添加有权重的边
'''
def add_edge(self, from_v, to_v, weight):
# 如果节点不存在
if from_v not in self.vert_list:
self.add_vertex(from_v)
if to_v not in self.vert_list:
self.add_vertex(to_v)
# from_v 节点的编号为行号,to_v 节点的编号为列号
self.matrix[from_v.v_id][to_v.v_id] = weight添加边信息的方法有 2 个,一个用来添加无权重边,一个用来添加有权重的边。
查找某节点
使用线性查找法从节点集合中查找某一个节点。
'''
根据节点编号返回节点
'''
def find_vertex(self, v_id):
if v_id >= 0 or v_id <= self.v_nums:
# 节点编号必须存在
return [tmp_v for tmp_v in self.vert_list if tmp_v.v_id == v_id][0]查询所有节点
'''
输出所有顶点信息
'''
def find_only_vertexes(self):
for tmp_v in self.vert_list:
print(tmp_v)此方法仅为了查询方便。
查询节点之间的关系
'''
迭代节点与节点之间的关系(边)
'''
def find_vertexes(self):
for tmp_v in self.vert_list:
edges = self.matrix[tmp_v.v_id]
for col in range(len(edges)):
w = edges[col]
if w != 0:
print(tmp_v, '和', self.vert_list[col], '的权重为:', w)测试代码:
if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称( q 为退出):")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
# 输出顶点及边a
print("-----------顶点与顶点关系--------------")
g.find_vertexes()
'''
输出结果:
顶点的名称( q 为退出):A
顶点的名称( q 为退出):B
顶点的名称( q 为退出):C
顶点的名称( q 为退出):D
顶点的名称( q 为退出):E
[编号为 0,名称为 A ] 的顶点 和 [编号为 1,名称为 B ] 的顶点 的权重为: 3
[编号为 0,名称为 A ] 的顶点 和 [编号为 3,名称为 D ] 的顶点 的权重为: 5
[编号为 1,名称为 B ] 的顶点 和 [编号为 2,名称为 C ] 的顶点 的权重为: 4
[编号为 2,名称为 C ] 的顶点 和 [编号为 3,名称为 D ] 的顶点 的权重为: 6
[编号为 2,名称为 C ] 的顶点 和 [编号为 4,名称为 E ] 的顶点 的权重为: 1
[编号为 3,名称为 D ] 的顶点 和 [编号为 4,名称为 E ] 的顶点 的权重为: 2
[编号为 4,名称为 E ] 的顶点 和 [编号为 1,名称为 B ] 的顶点 的权重为: 7
'''3. 搜索路径在图中经常做的操作,就是查找从一个顶点到另一个顶点的路径。如怎么查找到 A0 到 E4 之间的路径长度:

从人的直观思维角度查找一下,可以找到如下路径:
{A0,B1,C2,E4}路径长度为 8。{A0,D3,E4}路径长度为 7。{A0,B1,C2,D3,E4}路径长度为 15。
在路径查找时,人的思维具有知识性和直观性特点,因此不存在所谓的尝试或碰壁问题。而计算机是试探性思维,就会出现这条路不通,再找另一条路的现象。
所以路径算法中常常会以错误为代价,在查找过程中会走一些弯路。常用的路径搜索算法有 2 种:
广度优先搜索
深度优先搜索
先看一下广度优先搜索的示意图:

广度优先搜索的基本思路:
确定出发点,本案例是 A0 顶点。
以出发点相邻的顶点为候选点,并存储至队列。
从队列中每拿出一个顶点后,再把与此顶点相邻的其它顶点做为候选点存储于队列。
不停重复上述过程,至到找到目标顶点或队列为空。
使用广度搜索到的路径与候选节点进入队列的先后顺序有关系。如第 1 步确定候选节点时 B1 和 D3 谁先进入队列,对于后面的查找也会有影响。
上图使用广度搜索可找到 A0~E4 路径是:
{A0,B1,D3,C2,E4}
其实 {A0,B1,C2,E4} 也是一条有效路径,有可能搜索不出来,这里因为搜索到 B1 后不会马上搜索 C2,因为 B3 先于 C2 进入,广度优先搜索算法只能保证找到路径,而不能保存找到最佳路径。
编码实现广度优先搜索:
广度优先搜索需要借助队列临时存储选节点,本文使用列表模拟队列。
在图类中实现广度优先搜索算法的方法:
class Graph():
# 省略其它代码
'''
广度优先搜索算法
'''
def bfs(self, from_v, to_v):
# 查找与 fv 相邻的节点
self.find_neighbor(from_v)
# 临时路径
lst_path = [from_v]
# 重复条件:队列不为空
while len(self.queue_stack) != 0:
# 从队列中一个节点(模拟队列)
tmp_v = self.queue_stack.pop(0)
# 添加到列表中
lst_path.append(tmp_v)
# 是不是目标节点
if tmp_v.v_id == to_v.v_id:
self.searchPath.append(lst_path)
print('找到一条路径', [v_.v_id for v_ in lst_path])
lst_path.pop()
else:
self.find_neighbor(tmp_v)
'''
查找某一节点的相邻节点,并添加到队列(栈)中
'''
def find_neighbor(self, find_v):
if find_v.visited:
return
find_v.visited = True
# 找到保存 find_v 节点相邻节点的列表
lst = self.matrix[find_v.v_id]
for idx in range(len(lst)):
if lst[idx] != 0:
# 权重不为 0 ,可判断相邻
self.queue_stack.append(self.vert_list[idx])广度优先搜索过程中,需要随时获取与当前节点相邻的节点,find_neighbor() 方法的作用就是用来把当前节点的相邻节点压入队列中。
测试广度优先搜索算法:
if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称( q 为退出):")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
print("----------- 广度优先路径搜索--------------")
f_v = g.find_vertex(0)
t_v = g.find_vertex(4)
g.bfs(f_v,t_v)
'''
输出结果
顶点的名称( q 为退出):A
顶点的名称( q 为退出):B
顶点的名称( q 为退出):C
顶点的名称( q 为退出):D
顶点的名称( q 为退出):E
----------- 广度优先路径搜索--------------
找到一条路径 [0, 1, 3, 2, 4]
找到一条路径 [0, 1, 3, 2, 3, 4]
'''使用递归实现广度优先搜索算法:
'''
递归方式实现广度搜索
'''
def bfs_dg(self, from_v, to_v):
self.searchPath.append(from_v)
if from_v.v_id != to_v.v_id:
self.find_neighbor(from_v)
if len(self.queue_stack) != 0:
self.bfs_dg(self.queue_stack.pop(0), to_v)3.2 深度优先搜索算法先看一下深度优先算法的示意图。
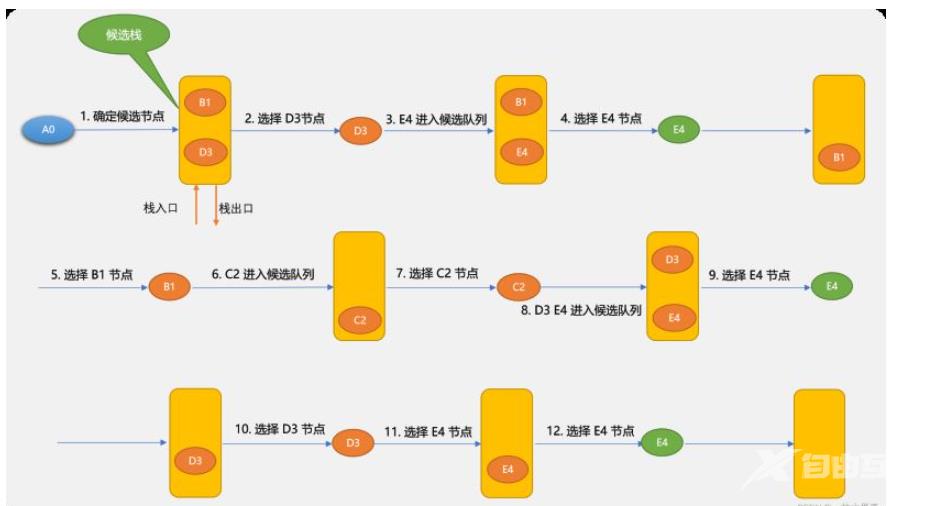
深度优先搜索算法和广度优先搜索算法不同的地方在于:深度优先搜索算法将候选节点放在堆栈中。因栈是先进后出,所以,搜索到的节点顺序不一样。
使用循环实现深度优先搜索算法:
深度优先搜索算法需要用到栈,本文使用列表模拟。
'''
深度优先搜索算法
使用栈存储下一个需要查找的节点
'''
def dfs(self, from_v, to_v):
# 查找与 from_v 相邻的节点
self.find_neighbor(from_v)
# 临时路径
lst_path = [from_v]
# 重复条件:栈不为空
while len(self.queue_stack) != 0:
# 从栈中取一个节点(模拟栈)
tmp_v = self.queue_stack.pop()
# 添加到列表中
lst_path.append(tmp_v)
# 是不是目标节点
if tmp_v.v_id == to_v.v_id:
self.searchPath.append(lst_path)
print('找到一条路径:', [v_.v_id for v_ in lst_path])
lst_path.pop()
else:
self.find_neighbor(tmp_v)测试:
if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称( q 为退出):")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
# 输出顶点及边a
print("-----------顶点与顶点关系--------------")
g.find_vertexes()
print("----------- 深度优先路径搜索--------------")
f_v = g.find_vertex(0)
t_v = g.find_vertex(4)
g.dfs(f_v, t_v)
'''
输出结果
顶点的名称( q 为退出):A
顶点的名称( q 为退出):B
顶点的名称( q 为退出):C
顶点的名称( q 为退出):D
顶点的名称( q 为退出):E
-----------顶点与顶点关系--------------
[编号为 0,名称为 A ] 的顶点 和 [编号为 1,名称为 B ] 的顶点 的权重为: 3
[编号为 0,名称为 A ] 的顶点 和 [编号为 3,名称为 D ] 的顶点 的权重为: 5
[编号为 1,名称为 B ] 的顶点 和 [编号为 2,名称为 C ] 的顶点 的权重为: 4
[编号为 2,名称为 C ] 的顶点 和 [编号为 3,名称为 D ] 的顶点 的权重为: 6
[编号为 2,名称为 C ] 的顶点 和 [编号为 4,名称为 E ] 的顶点 的权重为: 1
[编号为 3,名称为 D ] 的顶点 和 [编号为 4,名称为 E ] 的顶点 的权重为: 2
[编号为 4,名称为 E ] 的顶点 和 [编号为 1,名称为 B ] 的顶点 的权重为: 7
----------- 深度优先路径搜索--------------
找到一条路径: [0, 3, 4]
找到一条路径: [0, 3, 1, 2, 4]
'''使用递归实现深度优先搜索算法:
'''
递归实现深度搜索算法
'''
def def_dg(self, from_v, to_v):
self.searchPath.append(from_v)
if from_v.v_id != to_v.v_id:
# 查找与 from_v 节点相连的子节点
lst = self.find_neighbor_(from_v)
if lst is not None:
for tmp_v in lst[::-1]:
self.def_dg(tmp_v, to_v)
"""
查找某一节点的相邻节点,以列表方式返回
"""
def find_neighbor_(self, find_v):
if find_v.visited:
return
find_v.visited = True
# 查找与 find_v 节点相邻的节点
lst = self.matrix[find_v.v_id]
return [self.vert_list[idx] for idx in range(len(lst)) if lst[idx] != 0]递归实现时,不需要使用全局栈,只需要获到当前节点的相邻节点便可。
【文章原创作者:国外高防服务器 http://www.558idc.com/shsgf.html转载请说明出处】
