展示神经符号编程的力量
在过去的几年里,我们看到了基于 Transformer 的模型的兴起,并在自然语言处理或计算机视觉等许多领域取得了成功的应用。在本文中,我们将探索一种简洁、可解释和可扩展的方式来表达深度学习模型,特别是 Transformer,作为混合架构,即通过将深度学习与符号人工智能结合起来。因此,我们将在一个名为 PyNeuraLogic 的 Python 神经符号框架中来实现该模型。
通过将符号表示与深度学习相结合,我们填补了当前深度学习模型的空缺,例如可解释性的开箱即用和缺少推理技术。也许,增加参数的数量并不是实现这些预期结果的最合理方法,就像增加相机百万像素的数量不一定会产生更好的照片一样。
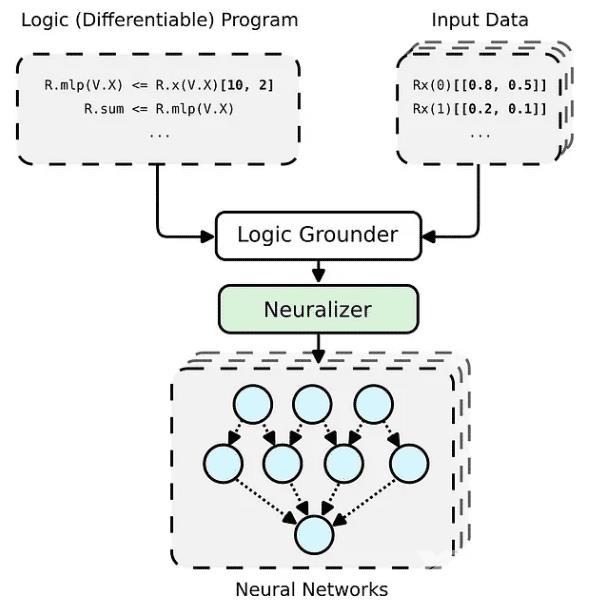
PyNeuraLogic 框架基于逻辑编程——逻辑程序包含可微分的参数。该框架非常适合较小的结构化数据(例如分子)和复杂模型(例如 Transformers 和图形神经网络)。PyNeuraLogic is not the best choice for non-relational and large tensor data.。
该框架的关键组成部分是一个可微分的逻辑程序,我们称之为模板。模板由以抽象方式定义神经网络结构的逻辑规则组成——我们可以将模板视为模型架构的蓝图。然后将模板应用于每个输入数据实例,以生成(通过基础和神经化)输入样本独有的神经网络。与其他预定义架构完全不同的是,这个过程无法自我调整以适应不同的输入样本。
2. Symbolic Transformers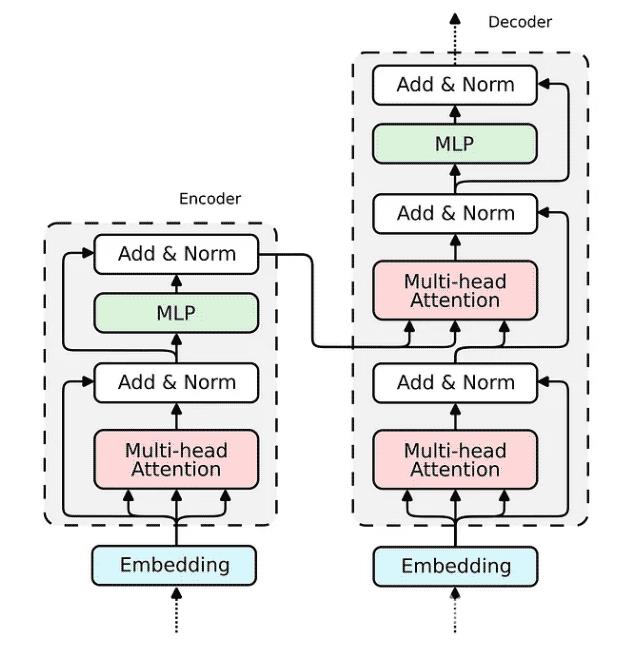
通常,我们会将深度学习模型实现为对批处理的输入令牌成一个大张量进行张量操作。这是有道理的,因为深度学习框架和硬件(例如 GPU)通常针对处理更大的张量而不是形状和大小不同的多个张量进行了优化。 Transformers 也不例外,通常将单个标记向量表示批处理到一个大矩阵中,并将模型表示为对此类矩阵的操作。然而,这样的实现隐藏了各个输入标记如何相互关联,这可以在 Transformer 的注意力机制中得到证明。
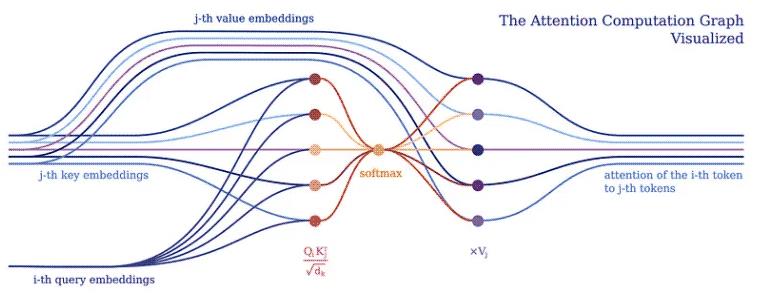
3. Attention 机制注意力机制构成了所有 Transformer 模型的核心。具体来说,它的经典版本使用了所谓的多头缩放点积注意力。让我们用一个头(为了清楚起见)将缩放的点积注意力分解成一个简单的逻辑程序。
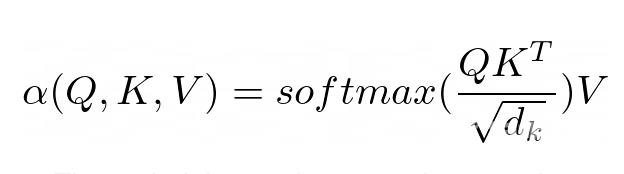
注意力的目的是决定网络应该关注输入的哪些部分。实现时需注意加权计算值 V,权重表示输入键 K 和查询 Q 的兼容性。在这个特定版本中,权重由查询 Q 和查询的点积的 softmax 函数计算键 K,除以输入特征向量维数 d_k 的平方根。
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]
在 PyNeuraLogic 中,我们可以通过上述逻辑规则充分捕捉注意力机制。第一条规则表示权重的计算——它计算维度的平方根倒数与转置的第 j 个键向量和第 i 个查询向量的乘积。接着,我们使用softmax函数将i与所有可能的j的结果进行聚合。
然后,第二条规则计算该权重向量与相应的第 j 个值向量之间的乘积,并对每个第 i 个标记的不同 j 的结果求和。
4. Attention Masking在训练和评估期间,我们通常会限制输入令牌可以参与的内容。例如,我们想限制标记向前看和关注即将到来的单词。流行的框架,例如 PyTorch,通过屏蔽实现这一点,即将缩放的点积结果的元素子集设置为某个非常低的负数。这些数字指定了强制 softmax 函数将相应标记对的权重设为零。
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],通过在我们的符号中添加身体关系约束,我们可以轻松地达到这一点。我们限制第 i 个指标大于或等于第 j 个指标,以计算权重。与掩码相反,我们只计算所需的缩放点积。
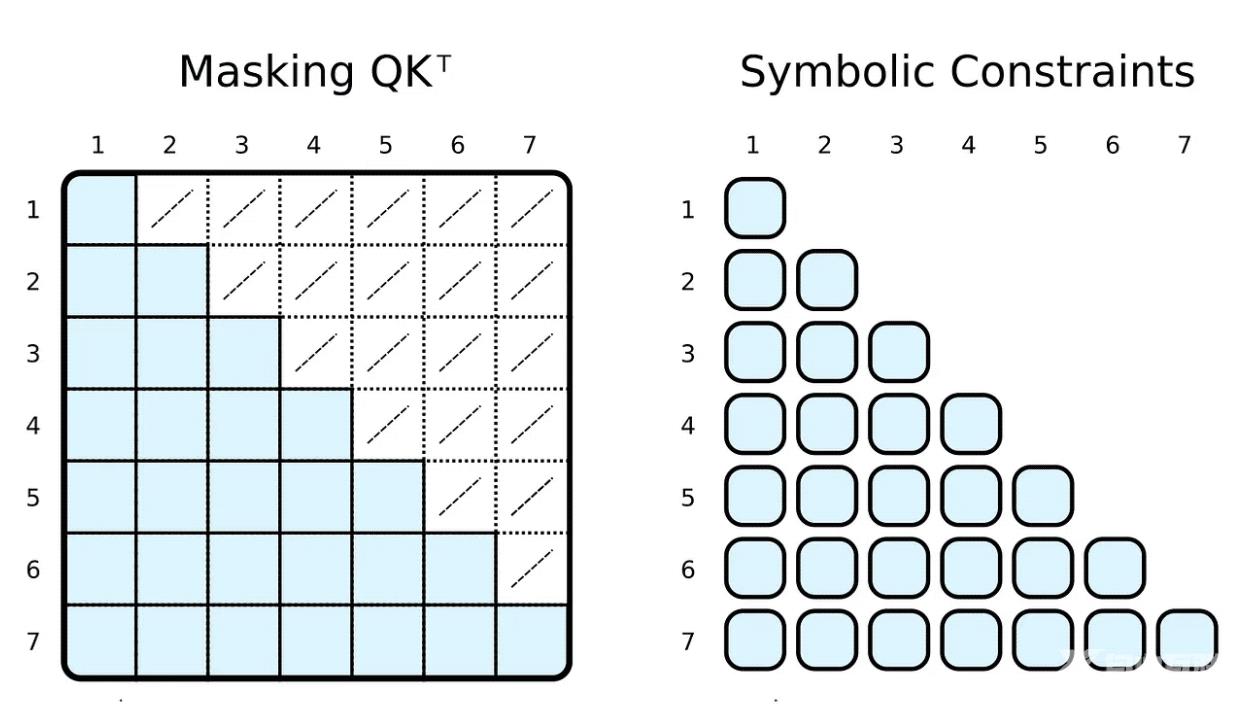
当然,象征性的“掩蔽”可以是完全任意的。大多数人都听过基于稀疏变换器的 GPT-3⁴,或其应用程序,例如 ChatGPT。⁵ 稀疏变换器的注意力(跨步版本)有两种类型的注意力头:
一个只关注前 n 个标记 (0 ≤ i − j ≤ n)
一个只关注每第 n 个前一个标记 ((i − j) % n = 0)
两种类型的头的实现都只需要微小的改变(例如,对于 n = 5)。
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],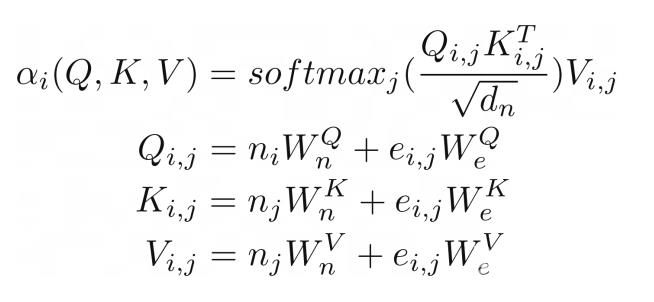
我们可以进一步推进,将类似图形输入的注意力概括到关系注意力的程度。⁶ 这种类型的注意力在图形上运行,其中节点只关注它们的邻居(由边连接的节点)。结果是节点向量嵌入和边嵌入的键 K、查询 Q 和值 V 相加。
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product], R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]), R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]), R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),
在我们的示例中,这种类型的注意力与之前展示的点积缩放注意力几乎相同。唯一的区别是添加了额外的术语来捕获边缘。将图作为注意力机制的输入似乎很自然,这并不奇怪,因为 Transformer 是一种图神经网络,作用于完全连接的图(未应用掩码时)。在传统的张量表示中,这并不是那么明显。
6. Encoder现在,当我们展示 Attention 机制的实现时,构建整个 transformer 编码器块的缺失部分相对简单。
如何在 Relational Attention 中实现嵌入已经为我们所展现。对于传统的 Transformer,嵌入将非常相似。我们将输入向量投影到三个嵌入向量中——键、查询和值。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v],
查询嵌入通过跳过连接与注意力的输出相加。然后将生成的向量归一化并传递到多层感知器 (MLP)。
(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],
对于 MLP,我们将实现一个具有两个隐藏层的全连接神经网络,它可以优雅地表达为一个逻辑规则。
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],
最后一个带有规范化的跳过连接与前一个相同。
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
所有构建 Transformer 编码器所需的组件都已经被构建完成。解码器使用相同的组件;因此,其实施将是类似的。让我们将所有块组合成一个可微分逻辑程序,该程序可以嵌入到 Python 脚本中并使用 PyNeuraLogic 编译到神经网络中。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v], R.d_k[1 / math.sqrt(embed_dim)], (R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product], (R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm], (R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu], (R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
【本文来源:美国服务器 http://www.558idc.com/mg.html提供,感恩】
