python排序算法之选择排序怎么实现

初级排序算法是指几种较为基础且容易理解的排序算法。初级排序算法包括插入排序、选择排序和冒泡排序3种。虽然它们的效率相对于高级排序算法偏低，但是在了解初级排序算法之后，再去学习相对复杂的高级排序算法会容易许多。

选择排序表示从无序的数组中，每次选择最小或最大的数据，从无序数组中放到有序数组的末尾，以达到排序的效果。

选择排序的平均时间复杂度是O(n2)，最好情况下的时间复杂度和最坏情况下的时间复杂度都是O( n2 )。另外，它是一个不稳定的排序算法。选择排序的过程很容易理解。以递增排序的算法为例，我们先遍历未排序的数组，在其中找到最小的元素，如图2-4所示。然后，将未排序数组中最小的元素删除，并将其添加到有序数组的末尾。

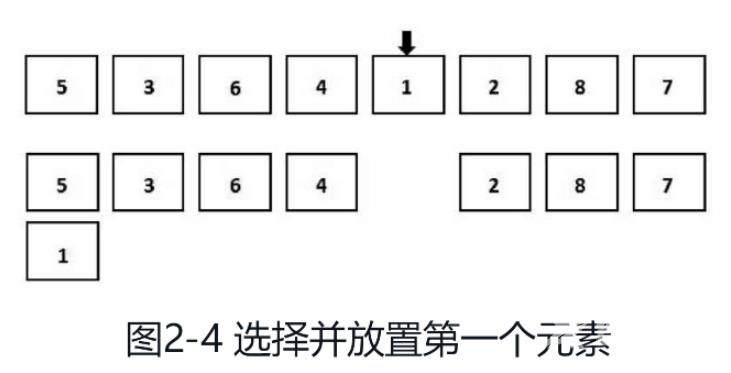
因为最小的元素是1，所以1被添加到仍为空的有序数组末尾。

如图2-5所示，我们继续对剩余元素进行遍历。这次，最小的元素是2。我们把它添加到已排序的数组末尾。这个操作是正确的，因为已排序数组中的元素一定比未排序数组中的元素小。

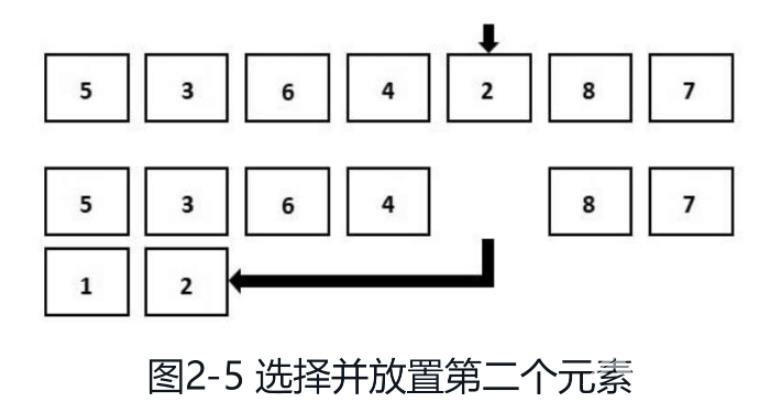
如图2-6所示，重复上述步骤，当未排序数组中只剩下一个元素时，把它添加到已排序的数组末尾，整个数组的排序就完成了。

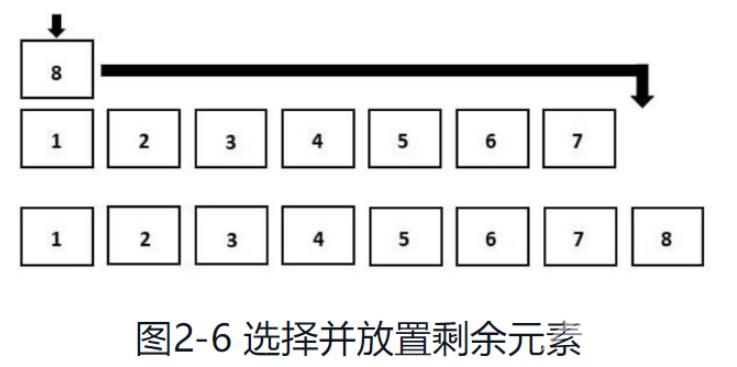
选择排序代码：

nums = [5,3,6,4,1,2,8,7]
res = []　　　#用于存储已排序元素的数组
while len(nums): #当未排序数组内还有元素时，重复执行选择最小数的代码
 minInd = 0 #初始化存储最小数下标的变量，默认为第一个数
 for i in range(1, len(nums)):
  if(nums[i] < nums[minInd]): #更新最小数的下标
    minInd = i
 temp = nums[minInd]
 nums.pop(minInd) #把最小数从未排序数组中删除
 res.append(temp) #把最小数插入到已排序数组的末尾
print(res)

运行程序，输出结果为：

[1,2,3,4,5,6,7,8]

在程序中，第一个for循环中的i代表了未排序数组中的第一个位置，即有序数组之后的第一个位置。随后，再使用一个for循环，在未排序数组中找到最小值的下标。初始时，将最小值下标minInd赋值为未排序数组的第一个元素的下标。当遇到比当前最小值更小的元素时，只需更新索引并遍历整个数组。把找到的最小值和未排序数组中的第一个元素进行交换后，最小值就被放到了有序数组的末尾位置。