XGBoost核心思想是多个基础模型的线性拟合,基础模型使用CART树(我喜欢),因为CART树普遍来讲要比线性基础模型的效果要好。
首先,xgboost采用的是加法训练,也就是要确定第t颗树最优,先确定第t-1颗树最优,依次类推。
所以,其目标函数:
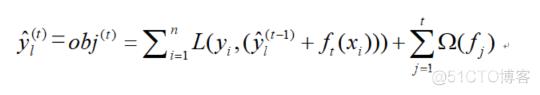
表示经过第t轮迭代后的模型预测值, 表示已知t-1个基础模型得到预测值; 表示第t个基础模型( ,w是叶子的向量、q是树的结构), 寻找一个使目标函数尽可能最大化降低的 ,那问题就解决了!因为前面的t-1颗树这时候已经固定了,找到 之后,模型主要求解部分基本结束,再把正则项化简, 即可求解。 为第j个正则化项,正则化惩罚项的目的是防止模型的复杂度与防止过拟合。根据泰勒展开式:
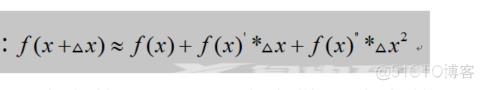
假设 为泰勒公式中的, ,L为泰勒公式中的f,损失函数的 为泰勒公式中的x,那么对于目标函数的求解一切将清晰明了:
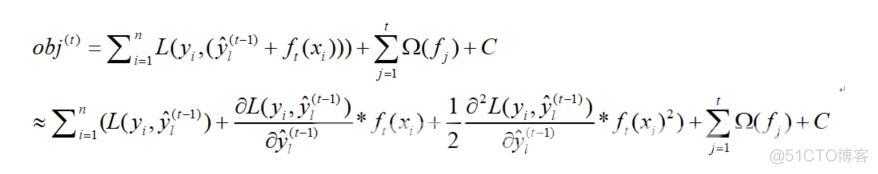
也就是说只要定义的损失函数可求一阶导和二阶导,那么只要再求解正则化项 出来,那么函数求解即可结束,即可开始考虑树结构的分割规则。
当然,如果使用最小二乘法作为损失,求导过程也就可以跳过,因为使用最小二乘法化简之后,一切将变得更加简单:
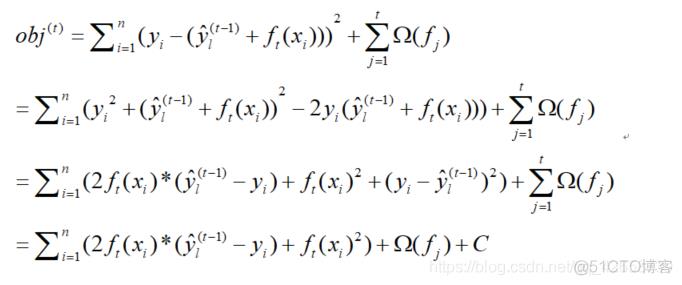
当然上面只是一个举例,其它的类似,虽然方法可能不再是最小二乘,但想法都是要把其进行化简,方便后面消去 。
其中,对于 来说, 是已知的,因为这个原理就是利用牛顿迭代法迭代出来的,只要第一个知道,后面迭代运算即可。由于 本质上是残差的平方,所以该项是一个常数。令其为C即可,后面再有常数直接与C合并即可,对模型并无影响。
Xgboost的基础模型 采取CART树,其实不管是预测还是回归,CART只有一个原理,只是在方式上有所不同,分类的时候采取了投票原则,回归的时候将叶子节点中的样本均值作为了该节点的预测值!对于回归,可以这样认为:假如自变量中X有n个观测,则计算相邻两个观测之间的均值 ,也就是说有(n-1)个均值,以均值为判断值将数据分为两部分, 为n1部分,反之为n2部分,这时候n1和n2中都分别含有两个分类的样本量,基尼指数下降速率为:
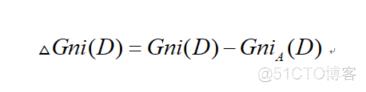
基尼指数下降速率表示了自变量对因变量的影响程度,下降越快影响越强。
CART树的字段选择指标是基尼指数 :
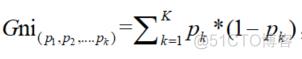
由基尼指数出发可以得到条件基尼指数 :
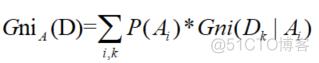
条件基尼指数采取二分法原理,以上用的概率都是用经验概率替代:
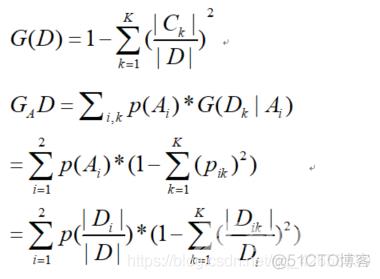
pk :某事件第k个可能值的发生概率,使用经验概率代替;
P(A)表示A变量在某个二元划分下第i组的概率,经验概率为A中第i组的样本量与总样本量的商。 表示 内变量D取第k种值的经验概率。
|D|:表示事件中的所有样本点, 那个除的式子表示事件的第k个可能值出现的次数。
该树由结构部分q和叶子节点对应的输出值w构成
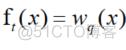
,T表示叶子节点的个数,则树的复杂度:
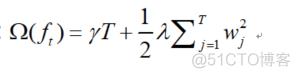
也就是说,T越多,树生长的越复杂。γ和λ是xgboost自己定义的,可以设定它们的值,γ越大,表示越希望获得结构简单的树,此时对较多叶子节点的树的惩罚越大。λ越大也是越希望获得结构简单的树。
将目标函数改写:
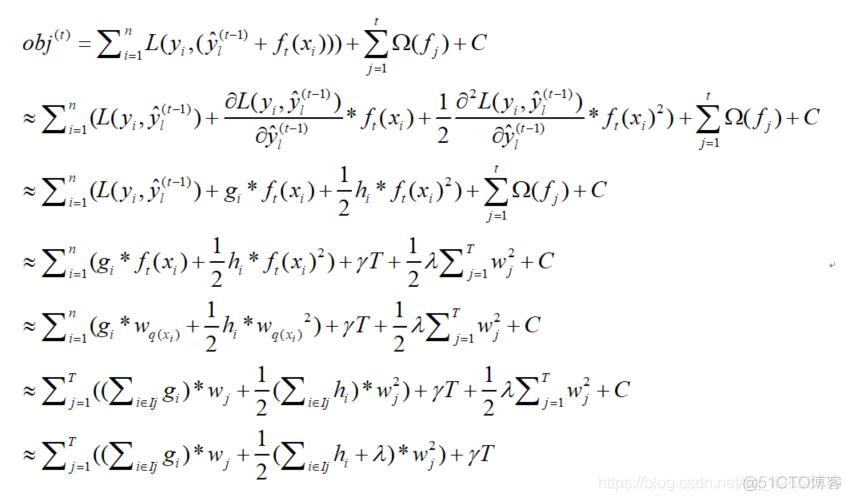
其中, 表示每个叶子节点j中所包含的样本集合, 表示第i个样本点的输入值 对应的输出值。这里一阶导使用 代替,二阶导使用 代替.
一样的道理,求偏导!对 求偏导,并令导函数为0。即:
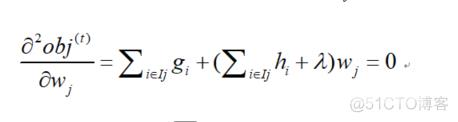
所以:
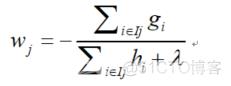
将 w代回obj ,得:

