C语言矩阵连乘 (动态规划)详解

动态规划法

题目描述：给定n个矩阵{A1,A2....An}，其中Ai与Ai+1是可以相乘的，判断这n个矩阵通过加括号的方式相乘，使得相乘的次数最少!

以矩阵链ABCD为例

按照矩阵链长度递增计算最优值

矩阵链长度为1时，分别计算出矩阵链A、B、C、D的最优值
矩阵链长度为2时，分别计算出矩阵链AB、BC、CD的最优值
矩阵链长度为3时，分别计算出矩阵链ABC、BCD的最优值
矩阵链长度为4时，计算出矩阵链ABCD的最优值

动归方程：

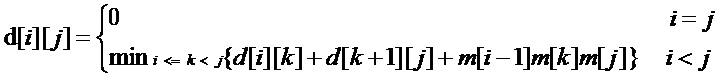
分析:

k为矩阵链断开的位置
d数组存放矩阵链计算的最优值，d[i][j]是以第i个矩阵为首，第j个矩阵为尾的矩阵链的最优值，i > 0
m数组内存放矩阵链的行列信息，m[i-1]和m[i]分别为第i个矩阵的行和列（i = 1、2、3...）

c语言实现代码：

#include <stdio.h>
#define N 20 
void MatrixChain(int p[N],int n,int m[N][N],int s[N][N]){ 
  int i,j,t,k;   
  int r;             //记录相乘的矩阵个数变量 
  for(i=1;i<=n;i++){ 
    m[i][i]=0;         //当一个矩阵相乘时，相乘次数为 0  
  }   
  //矩阵个数从两个开始一次递增  
  for(r=2;r<=n;r++){ 
    //从某个矩阵开始     
    for(i=1;i<=n-r+1;i++){ 
      //到某个矩阵的结束  
      j=i+r-1; 
      //拿到从 i 到 j 矩阵连乘的次数  
      m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; 
      //拿到矩阵连乘断开的位置  
      s[i][j]=i; 
      //寻找加括号不同，矩阵连乘次数的最小值，修改 m 数组，和断开的位置 s 数组  
      for(k=i+1;k<j;k++){ 
        t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]; 
        if(t<m[i][j]){ 
          m[i][j]=t; 
          s[i][j]=k; 
        } 
      } 
    } 
  }  
} 
 
int main(void){ 
  int n,n1,m1,i,j=2; 
  int p[N]={0};          //存储矩阵的行和列数组  
  int m[N][N]={0};        //存储矩阵与矩阵相乘的最小次数 
  int s[N][N]={0};        //存储矩阵与矩阵相乘断开的位置  
  printf("请输入矩阵个数:\n"); 
  scanf("%d",&n); 
  for(i=1;i<=n;i++){ 
    printf("请输入第%d个矩阵的行和列(n1*m1 格式):",i); 
    scanf("%d*%d",&n1,&m1); 
    if(i==1){ 
      p[0]=n1; 
      p[1]=m1; 
    } 
    else{ 
      p[j++]=m1; 
    } 
  } 
  printf("\n记录矩阵行和列:\n"); 
  for(i=0;i<=n;i++){ 
    printf("%d ",p[i]); 
  } 
  printf("\n"); 
  MatrixChain(p,n,m,s); 
  printf("\n矩阵相乘的最小次数矩阵为:\n"); 
  for(i=1;i<=n;i++){ 
    for(j=1;j<=n;j++){ 
      printf("%d  ",m[i][j]); 
    } 
    printf("\n"); 
  } 
  printf("\n矩阵相乘断开的位置矩阵为:\n"); 
  for(i=1;i<=n;i++){ 
    for(j=1;j<=n;j++){ 
      printf("%d ",s[i][j]); 
    } 
    printf("\n"); 
  } 
  printf("矩阵最小相乘次数为:%d\n",m[1][n]); 
  return 0; 
} 

感谢阅读，希望能帮助到大家，谢谢大家对本站的支持！