一、Torch与Numpy
Torch可以把tensor放到GPU加速上训练,就像Numpy把array放到CPU上训练一样。
torch tensor和numpy array的相互转换
tensor=torch.from_numpy(array)
array=tensor.numpy()
1 import torch 2 import numpy as np 3 4 np_data = np.arange(6).reshape((2, 3)) 5 torch_data = torch.from_numpy(np_data) 6 tensor2array = torch_data.numpy() 7 print( 8 ‘\nnumpy array:‘, np_data, # [[0 1 2], [3 4 5]] 9 ‘\ntorch tensor:‘, torch_data, # 0 1 2 \n 3 4 5 [torch.LongTensor of size 2x3] 10 ‘\ntensor to array:‘, tensor2array, # [[0 1 2], [3 4 5]] 11 )
Torch中的数学运算,np.数学函数 torch.数学函数一个样。
1 # abs 绝对值计算 2 data = [-1, -2, 1, 2] 3 tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor 4 print( 5 ‘\nabs‘, 6 ‘\nnumpy: ‘, np.abs(data), # [1 2 1 2] 7 ‘\ntorch: ‘, torch.abs(tensor) # [1 2 1 2] 8 ) 9 10 # sin 三角函数 sin 11 print( 12 ‘\nsin‘, 13 ‘\nnumpy: ‘, np.sin(data), # [-0.84147098 -0.90929743 0.84147098 0.90929743] 14 ‘\ntorch: ‘, torch.sin(tensor) # [-0.8415 -0.9093 0.8415 0.9093] 15 ) 16 17 # mean 均值 18 print( 19 ‘\nmean‘, 20 ‘\nnumpy: ‘, np.mean(data), # 0.0 21 ‘\ntorch: ‘, torch.mean(tensor) # 0.0 22 )
矩阵乘法 np.matmul和torch.mm一样
1 # matrix multiplication 矩阵点乘 2 data = [[1,2], [3,4]] 3 tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor 4 # correct method 5 print( 6 ‘\nmatrix multiplication (matmul)‘, 7 ‘\nnumpy: ‘, np.matmul(data, data), # [[7, 10], [15, 22]] 8 ‘\ntorch: ‘, torch.mm(tensor, tensor) # [[7, 10], [15, 22]] 9 ) 10 11 # !!!! 下面是错误的方法 !!!! 12 data = np.array(data) 13 print( 14 ‘\nmatrix multiplication (dot)‘, 15 ‘\nnumpy: ‘, data.dot(data), # [[7, 10], [15, 22]] 在numpy 中可行 16 ‘\ntorch: ‘, tensor.dot(tensor) # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0 17 )
在>=0.3.0版本中,tensor.dot()只能针对一维数组
1 tensor.dot(tensor) # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0 2 3 # 变为 4 torch.dot(tensor.dot(tensor)
二、变量
Torch里面的Variable就是一个鸡蛋篮子,里面的鸡蛋(tensor)在不停地变动如果用Variable进行计算,返回也是一个同类型的Variable
1 import torch 2 from torch.autograd import Variable # torch 中 Variable 模块 3 4 # 先生鸡蛋 5 tensor = torch.FloatTensor([[1,2],[3,4]]) 6 # 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度 7 variable = Variable(tensor, requires_grad=True) 8 9 print(tensor) 10 """ 11 1 2 12 3 4 13 [torch.FloatTensor of size 2x2] 14 """ 15 16 print(variable) 17 """ 18 Variable containing: 19 1 2 20 3 4 21 [torch.FloatTensor of size 2x2] 22 """
tensor和variable的计算没有什么不同。但是,Variable 计算时, 它在背景幕布后面一步步默默地搭建着一个庞大的系统, 叫做计算图, computational graph. 这个图是用来干嘛的? 原来是将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来, 而 tensor 就没有这个能力。
三、激励函数
y=AF(Wx)
AF是激励函数,掰弯神器,套在Wx上面,Wx就被掰弯了。
它其实就是另外一个非线性函数. 比如说relu, sigmoid, tanh. 将这些掰弯利器嵌套在原有的结果之上, 强行把原有的线性结果给扭曲了. 使得输出结果 y 也有了非线性的特征. 举个例子, 比如我使用了 relu 这个掰弯利器, 如果此时 Wx 的结果是1, y 还将是1, 不过 Wx 为-1的时候, y 不再是-1, 而会是0. 你甚至可以创造自己的激励函数来处理自己的问题, 不过要确保的是这些激励函数必须是可以微分的。
当你使用特别多层(三层以上)的神经网络, 在掰弯的时候, 玩玩不得随意选择利器. 因为这会涉及到梯度爆炸, 梯度消失的问题.
import torch import torch.nn.functional as F # 激励函数都在这 from torch.autograd import Variable # 一些假数据 x = torch.linspace(-5, 5, 200) x = Variable(x) # 几种常用的 激励函数 y_relu = F.relu(x) y_sigmoid = F.sigmoid(x) y_tanh = F.tanh(x) y_softplus = F.softplus(x) y_softmax = F.softmax(x) #softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类
四、线性回归
建立数据集
import torch import matplotlib.pyplot as plt x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1) y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1) # 画图 plt.scatter(x.data.numpy(), y.data.numpy()) plt.show()
建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层于层的关系链接. 建立关系的时候, 我们会用到激励函数。
1 import torch 2 import torch.nn.functional as F # 激励函数都在这 3 4 class Net(torch.nn.Module): # 继承 torch 的 Module 5 def __init__(self, n_feature, n_hidden, n_output): 6 super(Net, self).__init__() # 继承 __init__ 功能 7 # 定义每层用什么样的形式 8 self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出 9 self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出 10 11 def forward(self, x): # 这同时也是 Module 中的 forward 功能 12 # 正向传播输入值, 神经网络分析出输出值 13 x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值) 14 x = self.predict(x) # 输出值 15 return x 16 17 net = Net(n_feature=1, n_hidden=10, n_output=1) 18 19 print(net) # net 的结构 20 """ 21 Net ( 22 (hidden): Linear (1 -> 10) 23 (predict): Linear (10 -> 1) 24 ) 25 """
训练网络
1 # optimizer 是训练的工具 2 optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 传入 net 的所有参数, 学习率 3 loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差) 4 5 for t in range(100): 6 prediction = net(x) # 喂给 net 训练数据 x, 输出预测值 7 8 loss = loss_func(prediction, y) # 计算两者的误差 9 10 optimizer.zero_grad() # 清空上一步的残余更新参数值 11 loss.backward() # 误差反向传播, 计算参数更新值 12 optimizer.step() # 将参数更新值施加到 net 的 parameters 上
可视化训练过程
1 import matplotlib.pyplot as plt 2 3 plt.ion() # 画图 4 plt.show() 5 6 for t in range(200): 7 8 ... 9 loss.backward() 10 optimizer.step() 11 12 # 接着上面来 13 if t % 5 == 0: 14 # plot and show learning process 15 plt.cla() 16 plt.scatter(x.data.numpy(), y.data.numpy()) 17 plt.plot(x.data.numpy(), prediction.data.numpy(), ‘r-‘, lw=5) 18 plt.text(0.5, 0, ‘Loss=%.4f‘ % loss.data.numpy(), fontdict={‘size‘: 20, ‘color‘: ‘red‘})
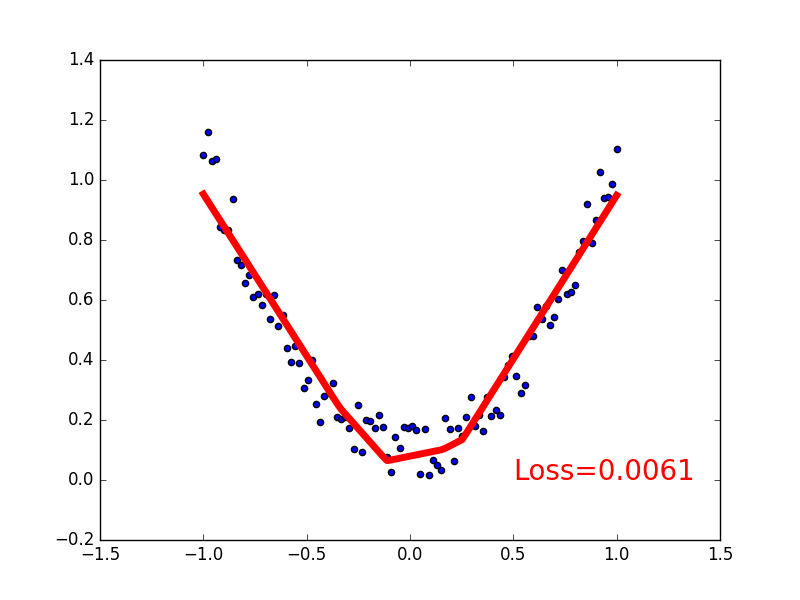
五、分类器
建立数据集
1 import torch 2 import matplotlib.pyplot as plt 3 4 # 假数据 5 n_data = torch.ones(100, 2) # 数据的基本形态 6 x0 = torch.normal(2*n_data, 1) # 类型0 x data (tensor), shape=(100, 2) 7 y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, ) 8 x1 = torch.normal(-2*n_data, 1) # 类型1 x data (tensor), shape=(100, 1) 9 y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, ) 10 11 # 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据) 12 x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating 13 y = torch.cat((y0, y1), ).type(torch.LongTensor) # LongTensor = 64-bit integer 14 15 # plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap=‘RdYlGn‘) 16 # plt.show() 17 18 # 画图 19 plt.scatter(x.data.numpy(), y.data.numpy()) 20 plt.show()
建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层于层的关系链接. 这个和我们在前面 regression 的时候的神经网络基本没差. 建立关系的时候, 我们会用到激励函数。
1 import torch 2 import torch.nn.functional as F # 激励函数都在这 3 4 class Net(torch.nn.Module): # 继承 torch 的 Module 5 def __init__(self, n_feature, n_hidden, n_output): 6 super(Net, self).__init__() # 继承 __init__ 功能 7 self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出 8 self.out = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出 9 10 def forward(self, x): 11 # 正向传播输入值, 神经网络分析出输出值 12 x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值) 13 x = self.out(x) # 输出值, 但是这个不是预测值, 预测值还需要再另外计算 14 return x 15 16 net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output 17 18 print(net) # net 的结构 19 """ 20 Net ( 21 (hidden): Linear (2 -> 10) 22 (out): Linear (10 -> 2) 23 ) 24 """
训练网络
1 # optimizer 是训练的工具 2 optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率 3 # 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,) 4 # 但是预测值是2D tensor (batch, n_classes) 5 loss_func = torch.nn.CrossEntropyLoss() 6 7 for t in range(100): 8 out = net(x) # 喂给 net 训练数据 x, 输出分析值 9 10 loss = loss_func(out, y) # 计算两者的误差 11 12 optimizer.zero_grad() # 清空上一步的残余更新参数值 13 loss.backward() # 误差反向传播, 计算参数更新值 14 optimizer.step() # 将参数更新值施加到 net 的 parameters 上
可视化
1 import matplotlib.pyplot as plt 2 3 plt.ion() # 画图 4 plt.show() 5 6 for t in range(100): 7 8 ... 9 loss.backward() 10 optimizer.step() 11 12 # 接着上面来 13 if t % 2 == 0: 14 plt.cla() 15 # 过了一道 softmax 的激励函数后的最大概率才是预测值 16 prediction = torch.max(F.softmax(out), 1)[1] 17 pred_y = prediction.data.numpy().squeeze() 18 target_y = y.data.numpy() 19 plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap=‘RdYlGn‘) 20 accuracy = sum(pred_y == target_y)/200. # 预测中有多少和真实值一样 21 plt.text(1.5, -4, ‘Accuracy=%.2f‘ % accuracy, fontdict={‘size‘: 20, ‘color‘: ‘red‘}) 22 plt.pause(0.1) 23 24 plt.ioff() # 停止画图 25 plt.show()
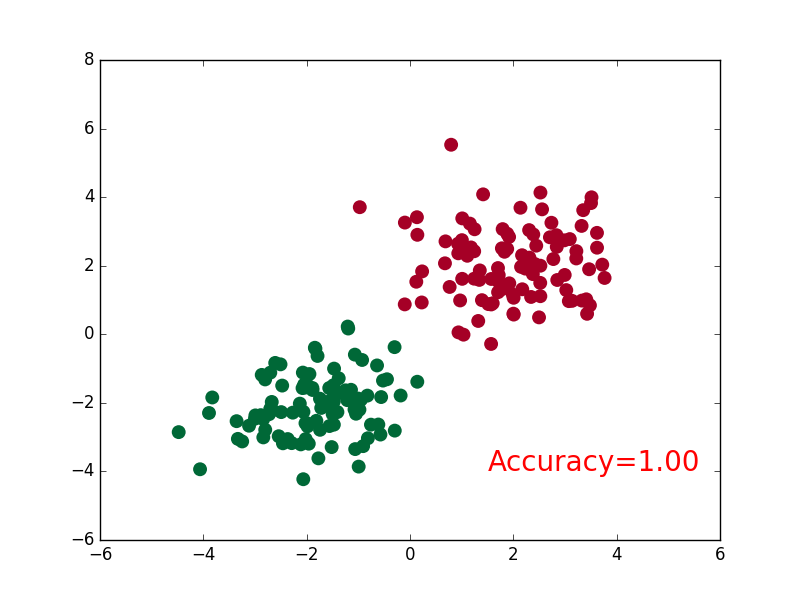
六、模型的保存、提取
建造数据、搭建网络
1 torch.manual_seed(1) # reproducible 2 3 # 假数据 4 x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1) 5 y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1) 6 7 def save(): 8 # 建网络 9 net1 = torch.nn.Sequential( 10 torch.nn.Linear(1, 10), 11 torch.nn.ReLU(), 12 torch.nn.Linear(10, 1) 13 ) 14 optimizer = torch.optim.SGD(net1.parameters(), lr=0.5) 15 loss_func = torch.nn.MSELoss() 16 17 # 训练 18 for t in range(100): 19 prediction = net1(x) 20 loss = loss_func(prediction, y) 21 optimizer.zero_grad() 22 loss.backward() 23 optimizer.step()
保存
1 torch.save(net1, ‘net.pkl‘) # 保存整个网络 2 torch.save(net1.state_dict(), ‘net_params.pkl‘) # 只保存网络中的参数 (速度快, 占内存少)
提取整个网络
1 def restore_net(): 2 # restore entire net1 to net2 3 net2 = torch.load(‘net.pkl‘) 4 prediction = net2(x)
只提取网络参数
1 def restore_params(): 2 # 新建 net3 3 net3 = torch.nn.Sequential( 4 torch.nn.Linear(1, 10), 5 torch.nn.ReLU(), 6 torch.nn.Linear(10, 1) 7 ) 8 9 # 将保存的参数复制到 net3 10 net3.load_state_dict(torch.load(‘net_params.pkl‘)) 11 prediction = net3(x)
显示结果
1 # 保存 net1 (1. 整个网络, 2. 只有参数) 2 save() 3 4 # 提取整个网络 5 restore_net() 6 7 # 提取网络参数, 复制到新网络 8 restore_params()
七、网络的快速搭建
我们用 class 继承了一个 torch 中的神经网络结构, 然后对其进行了修改, 不过还有更快的一招, 用一句话就概括了net1的内容
1 net2 = torch.nn.Sequential( 2 torch.nn.Linear(1, 10), 3 torch.nn.ReLU(), 4 torch.nn.Linear(10, 1) 5 )
两者结构
print(net1) """ Net ( (hidden): Linear (1 -> 10) (predict): Linear (10 -> 1) ) """ print(net2) """ Sequential ( (0): Linear (1 -> 10) (1): ReLU () (2): Linear (10 -> 1) ) """
我们会发现 net2 多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, 但是 net1 中, 激励函数实际上是在 forward() 功能中才被调用的. 这也就说明了, 相比 net2, net1 的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程
七、批训练
Dataloader整理数据结构,可以有效迭代数据
1 import torch 2 import torch.utils.data as Data 3 torch.manual_seed(1) # reproducible 4 5 BATCH_SIZE = 5 # 批训练的数据个数 6 7 x = torch.linspace(1, 10, 10) # x data (torch tensor) 8 y = torch.linspace(10, 1, 10) # y data (torch tensor) 9 10 # 先转换成 torch 能识别的 Dataset 11 torch_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y) 12 13 # 把 dataset 放入 DataLoader 14 loader = Data.DataLoader( 15 dataset=torch_dataset, # torch TensorDataset format 16 batch_size=BATCH_SIZE, # mini batch size 17 shuffle=True, # 要不要打乱数据 (打乱比较好) 18 num_workers=2, # 多线程来读数据 19 ) 20 21 for epoch in range(3): # 训练所有!整套!数据 3 次 22 for step, (batch_x, batch_y) in enumerate(loader): # 每一步 loader 释放一小批数据用来学习 23 # 假设这里就是你训练的地方... 24 25 # 打出来一些数据 26 print(‘Epoch: ‘, epoch, ‘| Step: ‘, step, ‘| batch x: ‘, 27 batch_x.numpy(), ‘| batch y: ‘, batch_y.numpy()) 28 29 """ 30 Epoch: 0 | Step: 0 | batch x: [ 6. 7. 2. 3. 1.] | batch y: [ 5. 4. 9. 8. 10.] 31 Epoch: 0 | Step: 1 | batch x: [ 9. 10. 4. 8. 5.] | batch y: [ 2. 1. 7. 3. 6.] 32 Epoch: 1 | Step: 0 | batch x: [ 3. 4. 2. 9. 10.] | batch y: [ 8. 7. 9. 2. 1.] 33 Epoch: 1 | Step: 1 | batch x: [ 1. 7. 8. 5. 6.] | batch y: [ 10. 4. 3. 6. 5.] 34 Epoch: 2 | Step: 0 | batch x: [ 3. 9. 2. 6. 7.] | batch y: [ 8. 2. 9. 5. 4.] 35 Epoch: 2 | Step: 1 | batch x: [ 10. 4. 8. 1. 5.] | batch y: [ 1. 7. 3. 10. 6.] 36 """
可以看出, 每步都导出了5个数据进行学习. 然后每个 epoch 的导出数据都是先打乱了以后再导出.如果我们改变一下 BATCH_SIZE = 8, 这样我们就知道, step=0 会导出8个数据, 但是, step=1 时数据不够则返回这个epoch中剩下的数据
八、优化器
为每个优化器建一种网络
1 # 默认的 network 形式 2 class Net(torch.nn.Module): 3 def __init__(self): 4 super(Net, self).__init__() 5 self.hidden = torch.nn.Linear(1, 20) # hidden layer 6 self.predict = torch.nn.Linear(20, 1) # output layer 7 8 def forward(self, x): 9 x = F.relu(self.hidden(x)) # activation function for hidden layer 10 x = self.predict(x) # linear output 11 return x 12 13 # 为每个优化器创建一个 net 14 net_SGD = Net() 15 net_Momentum = Net() 16 net_RMSprop = Net() 17 net_Adam = Net() 18 nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.
1 # different optimizers 2 opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR) 3 opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8) 4 opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9) 5 opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99)) 6 optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam] 7 8 loss_func = torch.nn.MSELoss() 9 losses_his = [[], [], [], []] # 记录 training 时不同神经网络的 loss
训练、出图
1 for epoch in range(EPOCH): 2 print(‘Epoch: ‘, epoch) 3 for step, (b_x, b_y) in enumerate(loader): 4 5 # 对每个优化器, 优化属于他的神经网络 6 for net, opt, l_his in zip(nets, optimizers, losses_his): 7 output = net(b_x) # get output for every net 8 loss = loss_func(output, b_y) # compute loss for every net 9 opt.zero_grad() # clear gradients for next train 10 loss.backward() # backpropagation, compute gradients 11 opt.step() # apply gradients 12 l_his.append(loss.data.numpy()) # loss recoder
九、卷积神经网络
CNN模型
这个 CNN 整体流程是 卷积(Conv2d) -> 激励函数(ReLU) -> 池化, 向下采样 (MaxPooling) -> 再来一遍 -> 展平多维的卷积成的特征图 -> 接入全连接层 (Linear) -> 输出
1 class CNN(nn.Module): 2 def __init__(self): 3 super(CNN, self).__init__() 4 self.conv1 = nn.Sequential( # input shape (1, 28, 28) 5 nn.Conv2d( 6 in_channels=1, # input height 7 out_channels=16, # n_filters 8 kernel_size=5, # filter size 9 stride=1, # filter movement/step 10 padding=2, # 如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2 当 stride=1 11 ), # output shape (16, 28, 28) 12 nn.ReLU(), # activation 13 nn.MaxPool2d(kernel_size=2), # 在 2x2 空间里向下采样, output shape (16, 14, 14) 14 ) 15 self.conv2 = nn.Sequential( # input shape (16, 14, 14) 16 nn.Conv2d(16, 32, 5, 1, 2), # output shape (32, 14, 14) 17 nn.ReLU(), # activation 18 nn.MaxPool2d(2), # output shape (32, 7, 7) 19 ) 20 self.out = nn.Linear(32 * 7 * 7, 10) # fully connected layer, output 10 classes 21 22 def forward(self, x): 23 x = self.conv1(x) 24 x = self.conv2(x) 25 x = x.view(x.size(0), -1) # 展平多维的卷积图成 (batch_size, 32 * 7 * 7) 26 output = self.out(x) 27 return output 28 29 cnn = CNN() 30 print(cnn) # net architecture 31 """ 32 CNN ( 33 (conv1): Sequential ( 34 (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) 35 (1): ReLU () 36 (2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1)) 37 ) 38 (conv2): Sequential ( 39 (0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) 40 (1): ReLU () 41 (2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1)) 42 ) 43 (out): Linear (1568 -> 10) 44 ) 45 """
训练
下面我们开始训练, 将 x y 都用 Variable 包起来, 然后放入 cnn 中计算 output, 最后再计算误差.省略了计算精确度 accuracy 的部分
1 optimizer = torch.optim.Adam(cnn.parameters(), lr=LR) # optimize all cnn parameters 2 loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted 3 4 # training and testing 5 for epoch in range(EPOCH): 6 for step, (b_x, b_y) in enumerate(train_loader): # 分配 batch data, normalize x when iterate train_loader 7 output = cnn(b_x) # cnn output 8 loss = loss_func(output, b_y) # cross entropy loss 9 optimizer.zero_grad() # clear gradients for this training step 10 loss.backward() # backpropagation, compute gradients 11 optimizer.step() # apply gradients 12 13 """ 14 ... 15 Epoch: 0 | train loss: 0.0306 | test accuracy: 0.97 16 Epoch: 0 | train loss: 0.0147 | test accuracy: 0.98 17 Epoch: 0 | train loss: 0.0427 | test accuracy: 0.98 18 Epoch: 0 | train loss: 0.0078 | test accuracy: 0.98 19 """
测试
1 test_output = cnn(test_x[:10]) 2 pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze() 3 print(pred_y, ‘prediction number‘) 4 print(test_y[:10].numpy(), ‘real number‘) 5 6 """ 7 [7 2 1 0 4 1 4 9 5 9] prediction number 8 [7 2 1 0 4 1 4 9 5 9] real number 9 """
十、GPU加速运算
修改的地方包括将数据的形式变成 GPU 能读的形式, 然后将 CNN 也变成 GPU 能读的形式. 做法就是在后面加上 .cuda()
1 test_data = torchvision.datasets.MNIST(root=‘./mnist/‘, train=False) 2 3 # !!!!!!!! 修改 test data 形式 !!!!!!!!! # 4 test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000].cuda()/255. # Tensor on GPU 5 test_y = test_data.test_labels[:2000].cuda()
再来把我们的 CNN 参数也变成 GPU 兼容形式.
1 class CNN(nn.Module): 2 ... 3 4 cnn = CNN() 5 6 # !!!!!!!! 转换 cnn 去 CUDA !!!!!!!!! # 7 cnn.cuda() # Moves all model parameters and buffers to the GPU.
然后就是在 train 的时候, 将每次的training data 变成 GPU 形式. + .cuda()
1 for epoch ..: 2 for step, ...: 3 # !!!!!!!! 这里有修改 !!!!!!!!! # 4 b_x = x.cuda() # Tensor on GPU 5 b_y = y.cuda() # Tensor on GPU 6 ... 7 if step % 50 == 0: 8 test_output = cnn(test_x) 9 # !!!!!!!! 这里有修改 !!!!!!!!! # 10 pred_y = torch.max(test_output, 1)[1].cuda().data.squeeze() # 将操作放去 GPU 11 accuracy = torch.sum(pred_y == test_y) / test_y.size(0) 12 ... 13 test_output = cnn(test_x[:10]) 14 # !!!!!!!! 这里有修改 !!!!!!!!! # 15 pred_y = torch.max(test_output, 1)[1].cuda().data.squeeze() # 将操作放去 GPU 16 ... 17 print(test_y[:10], ‘real number‘)
转移至CPU
1 cpu_data = gpu_data.cpu()
