【leetcode】1007. Minimum Domino Rotations For Equal Row

题目如下：

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the i-th domino.  (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i-th domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

 

Example 1:

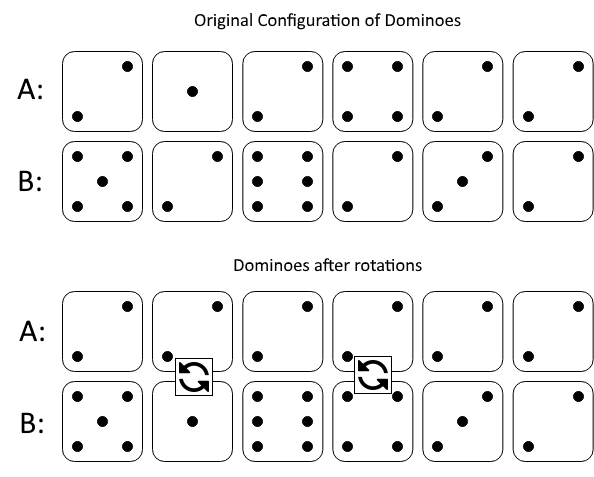
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2] Output: 2 Explanation: The first figure represents the dominoes as given by A and B: before we do any rotations. If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure. 

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4] Output: -1 Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal. 

 

Note:

1. 1 <= A[i], B[i] <= 6
2. 2 <= A.length == B.length <= 20000

解题思路：因为 1 <= A[i], B[i] <= 6，所以如果能使得A或者B中所有元素的值一样，那么就只有12种情况，即A中元素或者B中元素全为1/2/3/4/5/6，依次判断这6种情况即可，如假设变换后A中元素全为1，从头遍历A与B，如果A[i] != 1 并且B[i] != 1表示无法使得A中元素全为1，继续判断2的情况；否则如果A[i] != 1 并且B[i] = 1,那么交换的次数加1；同理可求得B中元素也全为1的交换次数。遍历完这6种情况后，如果无法满足则返回-1，可以的话返回交换的最小值。

代码如下：

class Solution(object):
    def minDominoRotations(self, A, B):
        """
        :type A: List[int]
        :type B: List[int]
        :rtype: int
        """
        res = 20001
        for i in range(1,7):
            a_move = 0
            b_move = 0
            a_flag = True
            b_flag = True
            for j in range(len(A)):
                if A[j] != i:
                    if B[j] != i:
                        a_flag = False
                    else:
                        a_move += 1
                if B[j] != i:
                    if A[j] != i:
                        b_flag = False
                    else:
                        b_move += 1
                if a_flag == False and b_flag == False:
                    break
            if a_flag:
                res = min(res,a_move)
            if b_flag:
                res = min(res,b_move)
        return res if res != 20001 else -1