一、递归概念
递归本质:程序调用自身的编程技巧叫做递归。
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调;
用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过;
程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。
二、递归的三个条件:
- 边界条件
- 递归前进段
- 递归返回段
当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
下面通过两个示例程序来说明:
使用Java代码求5的阶乘。(5的阶乘=5*4*3*2*1)
package org.wxp.recursion;
/**
* 计算5的阶乘(result = 5*4*3*2*1)
* @author Champion.Wong
*
*
*/
public class Test01 {
public static void main(String[] args) {
System.out.println(f(5));
}
public static int f(int n) {
if (1 == n)
return 1;
else
return n*f(n-1);
}
}
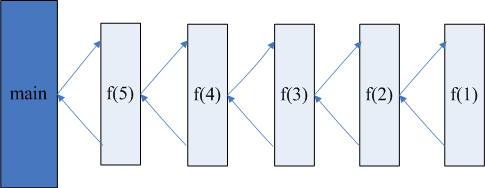
此题中,按照递归的三个条件来分析:
(1)边界条件:阶乘,乘到最后一个数,即1的时候,返回1,程序执行到底;
(2)递归前进段:当前的参数不等于1的时候,继续调用自身;
(3)递归返回段:从最大的数开始乘,如果当前参数是5,那么就是5*4,即5*(5-1),即n*(n-1)
使用Java代码求数列:1,1,2,3,5,8......第40位的数
package org.wxp.recursion;
/**
* 求数列:1,1,2,3,5,8......第40位的数
* @author Champion.Wong
*
*/
public class Test_02_Fibonacci {
public static void main(String[] args) {
System.out.println(f(6));
}
public static int f(int n ) {
if (1== n || 2 == n)
return 1;
else
return f(n-1) + f(n-2);
}
}
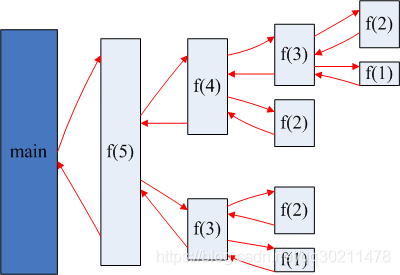
此题的突破口在:从第3位数开始,本位数是前两位数的和。要计算第多少位的值,那么就需要将位数作为参数传进方法进行计算。
(1)首先,当位数为1和2时,当前返回的值应该是1;
(2)然后,当位数为3时,返回值应该=2=1+1;
当位数为4时,返回值=3=2+1;
当位数为5时,返回值=5=3+2;
当位数为6时,返回值=8=5+3;
......
(3)由(2)得知,大于等于3的情况下,当前位数(n)的数值=f(n-1)+f(n-2)
三、非递归方法实现(迭代方法)
迭代本质:利用变量的原值推算出变量的一个新值,迭代就是A不停的调用B.
通过观察推导,找到解决问题的方法,发现其中的规律,将其转化成程序语言表达出来。
本质:使用合适的数据类型变量代替问题中的数据,将解决问题的方法转化为符合程序语言的逻辑。
public class Fab{
public static void main( String[] args){
System.out.println(f(20));
}
public static long f(int index){
if(index == 1 || index == 2){
return 1;
}
long f1 = 1L;
long f2 = 1L;
long f = 0;
for(int i=0; i<index; i++){
f = f1 + f2;
f1 = f2;
f2 = f;
}
return f;
}
}
递归其实是方便了程序员难为了机器,递归可以通过数学公式很方便的转换为程序。其优点就是易理解,容易编程。但递归是用栈机制实现的,每深入一层,都要占去一块栈数据区域,对嵌套层数深的一些算法,递归会力不从心,空间上会以内存崩溃而告终,而且递归也带来了大量的函数调用,这也有许多额外的时间开销。所以在深度大时,它的时空性就不好了。(会占用大量的内存空间)
而迭代虽然效率高,运行时间只因循环次数增加而增加,没什么额外开销,空间上也没有什么增加,但缺点就是不容易理解,编写复杂问题时困难。
能不用递归就不用递归,递归都可以用迭代来代替。(要辩证的看待这个问题,深度不大,还是可以采用递归的)。
总结
到此这篇关于java新人基础入门之递归调用的文章就介绍到这了,更多相关java递归调用内容请搜索易盾网络以前的文章或继续浏览下面的相关文章希望大家以后多多支持易盾网络!
