Java青蛙跳台阶问题的解决思路与代码

问题描述

一只青蛙一次可以跳上1级台阶，也可以一次跳上2级台阶，请问跳上n级台阶，该请娃一共有多少种跳法？

解决思路

①如果只有1级台阶，那显然只有一种跳法。

②如果有2级台阶，那么就有2种跳法，一种是分2次跳。每次跳1级，另一种就是一次跳2级。

③如果台阶级数大于2，设为n的话，这时我们把n级台阶时的跳法看成n的函数，记为,第一次跳的时候有2种不同的选择：一是第一次跳一级，此时跳法的数目等于后面剩下的n-1级台阶的跳法数目，即为,二是第一次跳二级，此时跳法的数目等于后面剩下的n-2级台阶的跳法数目，即为,因此n级台阶的不同跳法的总数为，不难看出就是斐波那契数列。

实现代码

1.青蛙跳台阶递归方法
 public static int f1(int n){
 if(n==1||n==2){
 return n;
 }
 else{
 return f1(n-1)+f1(n-2);
 }
 }

2.青蛙跳台阶非递归方法
 public static int f2(int m){
 if(m==1||m==2){
 return m;
 }
 int a1 = 1;
 int a2 = 2;
 int result = 0;

 for (int i = 3; i <= m; i++) {
 result = a1 + a2;
 a1 = a2;
 a2 = result;
 }
 return result;
 }

 public static void main(String[] args) {
 Scanner sc = new Scanner(System.in);
 int num = sc.nextInt();
 System.out.println("递归青蛙跳"+num+"级台阶共有"+f1(num)+"种方法!");
 System.out.println("非递归青蛙跳"+num+"级台阶共有"+f2(num)+"种方法!");
 }

运行结果：

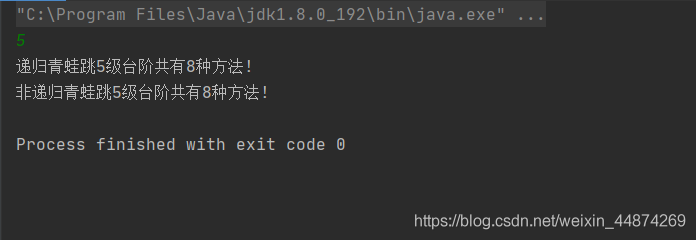
总结

到此这篇关于Java青蛙跳台阶问题的解决思路与代码的文章就介绍到这了,更多相关Java青蛙跳台阶内容请搜索易盾网络以前的文章或继续浏览下面的相关文章希望大家以后多多支持易盾网络！