Python数据结构之树的全面解读

目录

• 前言
• 🧡基本概念
• 🌳树的定义
• 🌲基本术语
• 💚树的逻辑结构
• 🍉前序遍历
• 🍓后序遍历
• 🍒层序遍历
• 💜树的存储结构
• 🍀双亲表示法
• 🍁孩子链表表示法
• 🍃双亲孩子表示法
• 🍂孩子兄弟表示法
• 总结

前言

提示：以下是本篇文章正文内容

🧡基本概念

🌳树的定义

树是n（n≥0）个结点的有限集合，n = 0时，称为空树，这是一种特殊情况

在任意一棵非空树中应满足：
①有且仅有一个特定的称为根的结点
②当n > 1时，其余结点可分为m（m > 0）个互不相交的有限集合T1，T2，…，Tm，其中每个集合本身又是一棵树，并且称为根结点的子树==

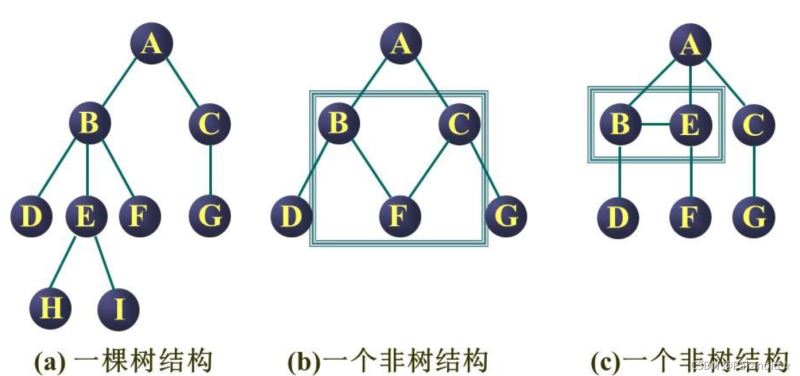
∅ 空树——结点数为0的树

非空树的特性：

有且仅有一个根节点
除了根节点外，任何一个结点都有且仅有一个前驱
每个结点可以有0个或多个后继

🌲基本术语

1.度

(1)结点的度：结点所拥有的子树的个数

(2)树的度：树中各结点度的最大值

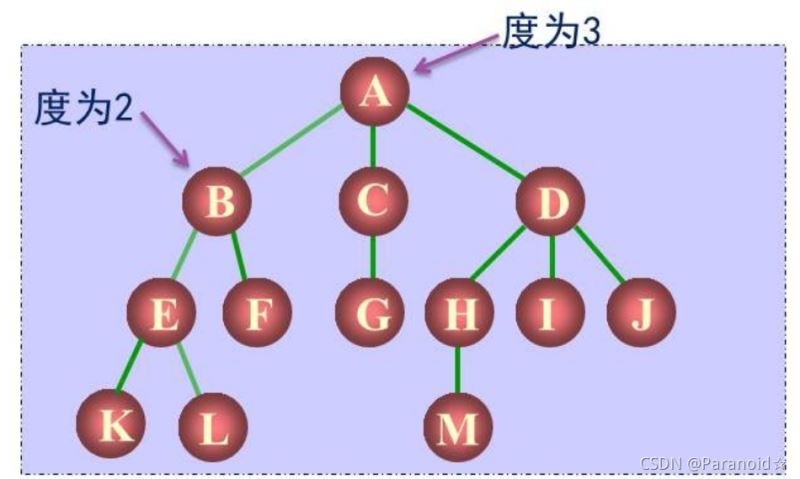
A的度为3，同时也是树的度，B的度为2

2.叶子节点和分支节点
(1)叶子节点
度为0的节点，也称为终端结点

(2)分支节点
度不为0的节点，也称为非终端结点

在上图中，K,L,M,F,G,I,J均为叶子节点

3.双亲与孩子
(1)祖先结点：对于任何节点n ，它的祖先是位于根到节点n之间的路径上的节点

(2)子孙结点：一个结点含有的子树的根结点的子节点

在树中，如果有一条路径从节点x到节点y,则称x为y的祖先，y为x的子孙

(3)双亲结点（父节点）：若一个结点含有子结点，则这个结点称为其子结点的父节点

(4)孩子结点：一个结点含有的子树的根结点称为该结点的子结点

(5)兄弟结点：具有相同父结点的结点互称为兄弟结点

(6)堂兄弟结点：如果树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点
B,C,D互为兄弟节点，E,G,I互为堂兄弟节点，B为E,F的父节点，而E,F为B的子节点

(4)树的深度
节点所在层数：根节点的层数为1，对于其他任何节点，若某节点在第K层，则其孩子节点在K+1层

树的深度：树中所有节点的最大层数，也称为高度
在上图中，树的深度为4

(5)树的类型
有序树：树中结点的各子树从左至右是有次序的，不能互换
无序树：树中结点的各子树从左至右是无次序的，可以互换

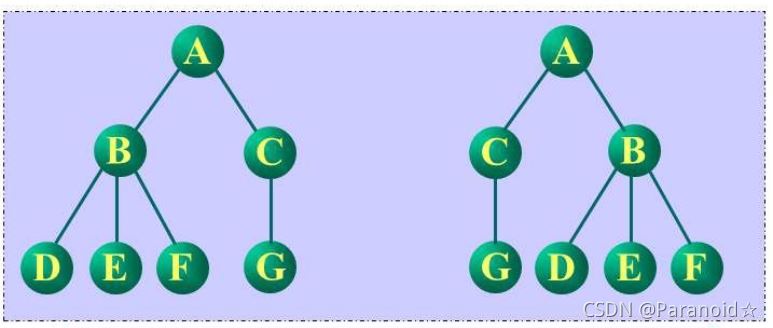
注：在数据结构中，一般的讨论的一般是有序树

(6)森林
森林是m（m≥0）棵互不相交的树的集合，m可为0，空森林

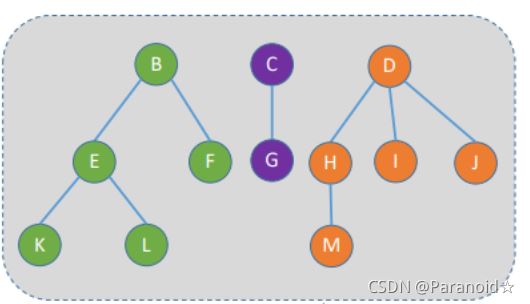
💚树的逻辑结构

树的遍历：从根节点出发，按照某种次序访问树中所有的节点，使得每个节点被访问一次且仅被访问一次

访问：抽象操作，可以是对节点进行的各种处理，这里简化为输出节点的数据

遍历的实质：树的结构(非线性结构) – > 线性结构

树通常有前序(根)遍历，后序(根)遍历，层序(次)遍历三种

🍉前序遍历

树的前序遍历操作定义为：若树为空，则空操作返回；否则:
(1)先访问根节点
(2)然后按照从左到右的顺序前序遍历根节点的每一颗子树

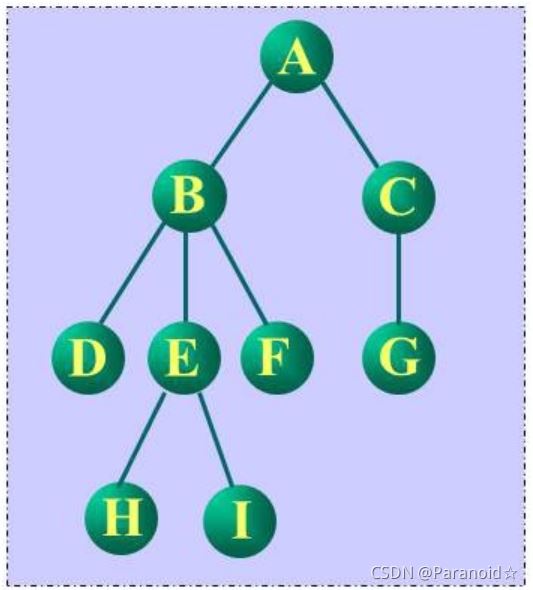
如图前序遍历序列：A–>B–>D–>E–>H–>I–>F–>C–>G

🍓后序遍历

树的后序遍历操作定义为：若树为空，则空操作返回；否则:
(1)先按照从左到右的顺序后序遍历根节点的每一颗子树
(2)最后访问根节点

如图后序遍历序列：D–>H–>I–>E–>F–>B–>G–>C–A

🍒层序遍历

树的层序遍历操作定义为：从树的第一层(即根节点）开始，自上而下的逐层遍历，在同一层中，按照从左到右的顺序对节点逐个访问

如图层序遍历序列：A–>B–>C–>D–>E–>F–>G–>H–>I

💜树的存储结构

实现树的存储结构，关键在于表示树中的节点之间的关系

🍀双亲表示法

基本思想：用一维数组来存储树的各个节点（一般按层序存储），数组中的一个元素对应树中的一个节点，包括节点的数据信息和节点的双亲在数组中的下标。

节点结构

struct PNode
{
	DataType data; //数据域
	int parent;   //指针域，双亲在数组中的下标
}

树的双亲表示法实质上是一个静态链表
如图所示：

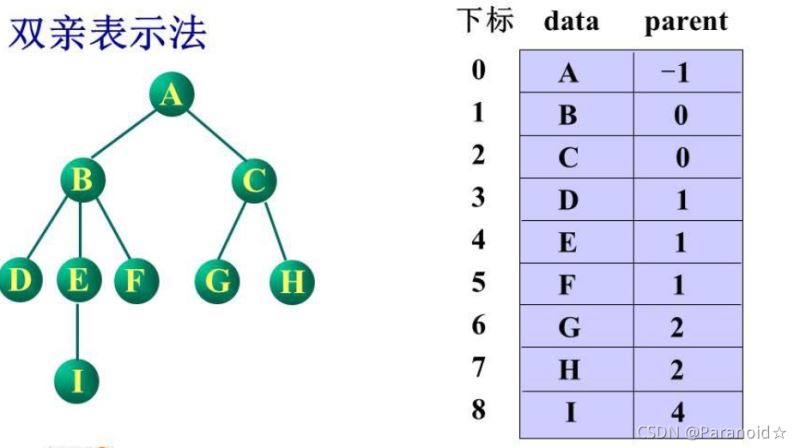
还可以将孩子节点或者兄弟节点的下标也进行存储

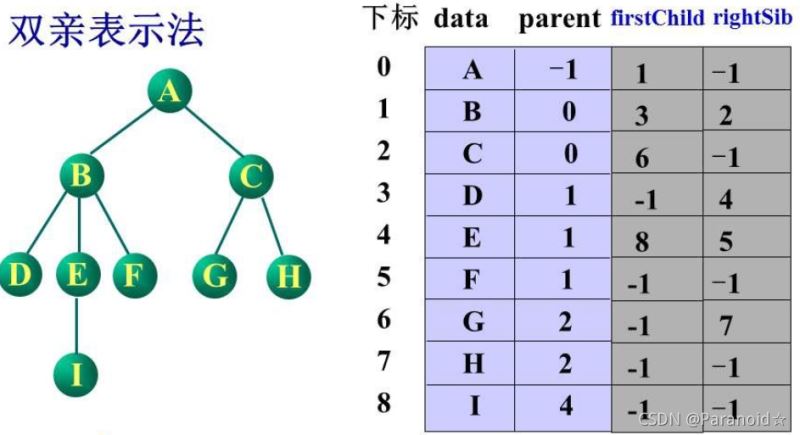
🍁孩子链表表示法

将结点的所有孩子放在一起，构成线性表

基本思想：把每个结点的孩子排列起来，看成是一个线性表，且以单链表存储，则n个结点共有n个孩子链表。这n个单链表共有n个头指针，这n个头指针又组成了一个线性表,为了便于进行查找采用顺序存储。最后, 将存放n个头指针的数组和存放n个结点的数组结合起来，构成孩子链表的表头数组

链表中的每个节点包含一个数据域和多个指针域，每个指针域指向该节点的一个孩子节点

方案一：
指针域的个数等于树的深度

缺点：浪费存储空间

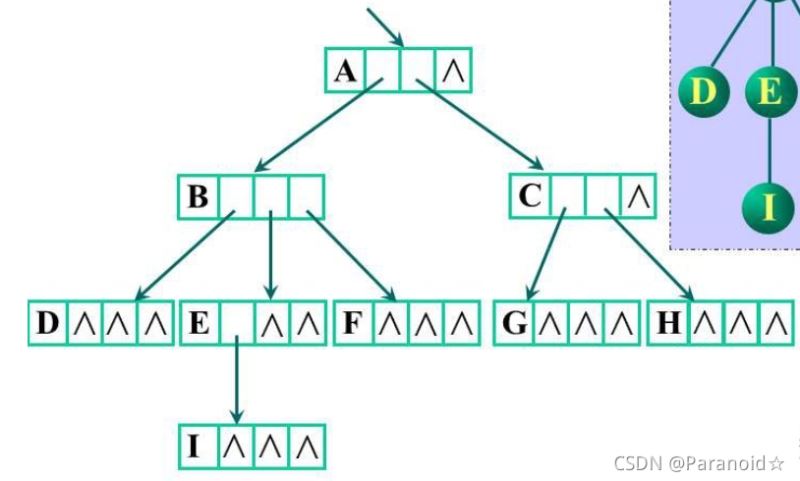
方案二：
指针域的个数等于该结点的度

缺点：每个结点结构不一致

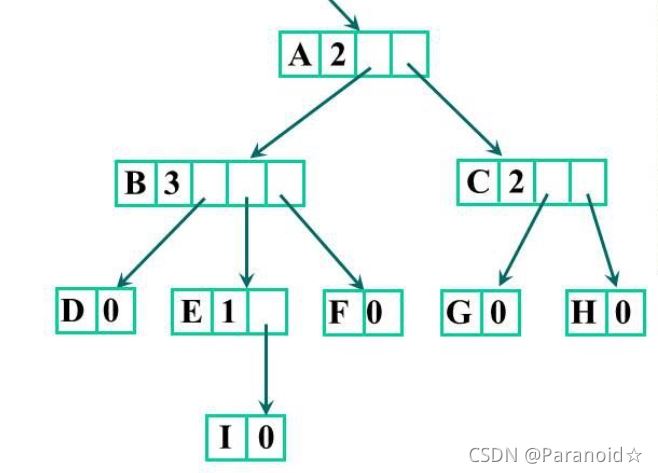
孩子节点

struct CTNode
{
	int child;
	CTNode *next; // 指向下一个孩子结点的指针
}

表头结点

struct CBNode
{
	DataType data;
	CTNode *firstChild; // 每个链表的头指针
}

存储结构

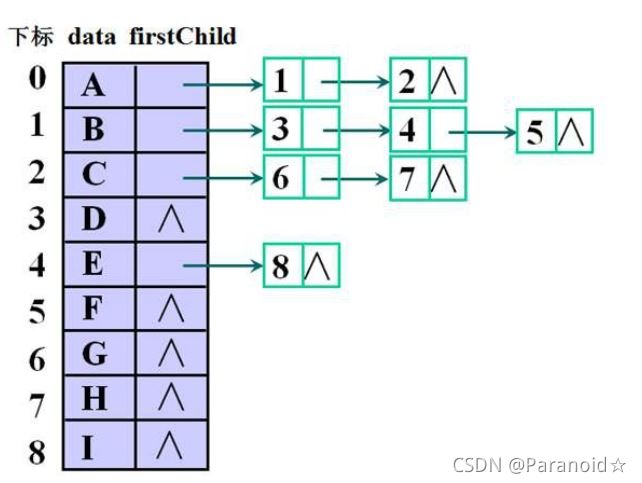
🍃双亲孩子表示法

在孩子链表中表头数组添加了节点的双亲结点

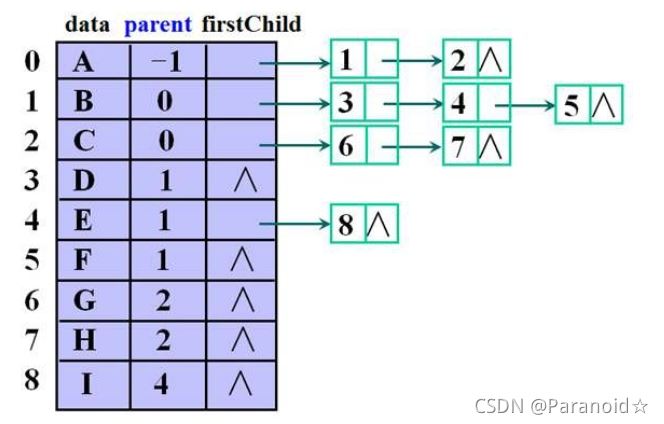
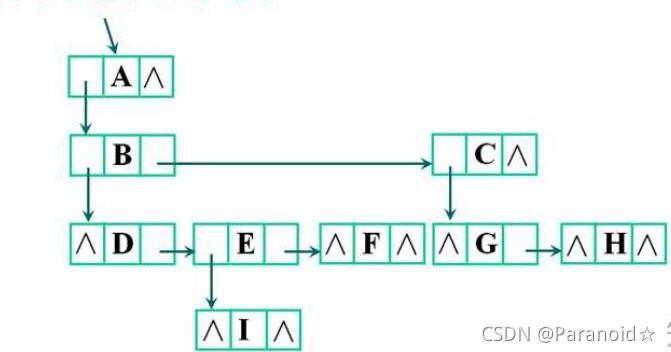
🍂孩子兄弟表示法

某节点的第一个孩子是唯一的，某一节点的右兄弟是唯一的，设置两个分别指向该节点的第一个孩子和右兄弟的指针

struct TNode
{
	DataType data;
	TNode *firstChild,*rightSib;
}

总结

提示：这里对文章进行总结：

到此这篇关于Python数据结构之树的全面解读的文章就介绍到这了,更多相关Python 数据结构内容请搜索易盾网络以前的文章或继续浏览下面的相关文章希望大家以后多多支持易盾网络！