编程思想板块最主要的内容是数据结构经典题目及解答题目所需的编程思想，愿对您能有所帮助
一、顺序表和链表
① 若以线性表表示集合并进行集合的各种运算，应先对表中元素进行排序
② 常考将两个有序链表合成一个新的有序表
③ 在这一章中哈希表的思想很常用
④ 注意：代码后记得要更新length值
⑤ 逆置的常见方法：
(1) 头插法
(2) 递归
(3) 借助栈
⑥ 链表中：
(1) 前插操作时：将待插入结点s依旧插入P后面，然后交换s和p的值，此时时间复杂度为O(1)
(2) 删除结点p：将后继结点的值赋给自己p，然后删除后继结点，此时时间复杂度为O(1)
(3) 若题目中只要求在时间上尽可能高效，则采用空间换时间的方法
1）顺序表经典题目的编程思想1. 对长度为n的顺序表L,编写一个时间复杂度为O(n)、空间复杂度为0(1)的算法，该算法删除线性表中所有值为x的数据元素（经典的顺序表删除元素的方法）
思想：
① 用k记录顺序表L中不等于x的元素个数(即需要保存的元素个数)，边扫描L边统计k，并将不等于x的元数向前移动k个位置（初始k=0），最后修改L的长度
② 用k记录顺序表L中等于x的元素个数，边扫描L边统计k，并将不等于x的元素前移k个位置,最后修改L的长度
2. 从有序顺序表中删除所有其值重复的元素，使表中所有元素的值均不同（若为无序的可用哈希表解决）
思想：
① 用类似于直接插入排序的思想，初始时将第一个元素视为非重复的有序表。之后依次判断后面的元素是否与前面非重复有序表的最后一个元素相同，若相同，则继续问后判断，若个同,则插入前面的非重复有序表最后,直至判断到表尾为止
3. 将两个有序顺序表合并为一个新的有序顺序表，并由函数返回结果顺序表
思想：
① 首先，按顺序不断取下两个顺序表表头较小的结点存入新的顺序表中。然后，看哪个表还有剩余，将剩下的部分加到新的癞序表后面
4. 已知在一维数组A[m+n]中依次存放两个线性表(a,a2,...,am)和(b1,b2,b3,..,bn)。试编写一个函数,将数组中两个顺序表的位置互换，即将(b1,b2,b3,..,bn)放在(a,a2,...,am)的前面
思想：
① 
5.
思想：
6. 一个长度为L(L≥1)的升序序列S，处在第向上取整（L/2）个位置的数称为S的中位数。例如，若序列S1=(11,13,15,17,19)则S1的中位数是15,两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若S2=(2,4,6,8, 20)，则S1和S2的中位数是11.现在有两个等长升序序列A和B,试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数
思想：
① 分别求两个升序序列A、B的中位数，设为a和b，求序列A、B的中位数过程如下
（1) 若a<b，则舍弃序列A中较小的一半，同时舍弃序列B中较大的一半，要求两次舍弃长度相等
（2) 若a>b、则舍弃序列A中较大的一半，同时舍弃序列B中较小的--半，要求两次舍弃的长度相等
（3) 若a=b，则α或b即为所求中位数，算法结束
（4) 在保留的两个升序序列中，重复过程①、②、③,直到两个序列中均只含一个元素时为止,较小者即为所求的中位数
7. 已知一个整数序列A=(a_0,a_1,...,a_(n-1)),其中0≤a_i<n(0≤i<n)。若存在a_p1=a_p2=...=a_pm=x且m>n/2(0≤P_k<n,1<=k<=m),则称x为A的主元素。例如A=(0,5,5,3,5,7,5,5)，则5为主元意;又如A=(0,5,5,3,5,1,5,7)，则A中没有主元素。假设A中的n个元素保存在一个一维数组中，请设计一个尽可能高效的算法，找出A的主元素。若存在主元素，则输出该元素;否则输出-1（该思想也可用于求数组最长子序列（数组数据包括负数和正数））
思想：
① 给出算法的基本设计思想:算法的策略是从前向后扫描数组元繁，杯记出一个可能成为主元素的元素Num。然后重新计数，确认 Num是否是主元素。算法可分为以下两步:（摩尔投票法）
（1) 选取候选的主元素。依次扫描所给数组中的每个整数，将第一个遇到的整数Num保存到c中，记录 Num 的出现次数为1;若遇到的下一个整数仍等于 Num，则计数加1，否则计数减1:当计数减到0时,将遇到的下一个整数保存到c中，计数重新记为1，开始新一轮计数，即从当前位置开始重复上述过程，直到扫描完全部数组元素
（2) 判断c中元素是否是真正的主元素。再次扫描该数组，统计c中元素出现的次数，若大于n/2，则为主元素:否则，序列中不存在主元素
8. 给定一个含n(n≥I)个整数的数组，请攻订一个杜时间一公马)向效的算法，找出数组中未出现的最小正整数。例如，数组{-5,3,2,3}中未出现的最小正整数是l;数组{1,2,3}中未出现的最小正整数是4
思想：
① 要求在时间上尽可能高效，因此采用空问换时间的办法。分配一个用于标记的数组B[n]用来记录A中是否出现了1~n中的正整数，B[0]对应正整数1，B[n-1]对应正整数n，初始化B中全部为0。由于A中含有n个整数，因此可能返回的值是 1n+1，当A中n个数恰好为1n 时返回n+1。当数组A中出现了小于等于0或大于n的值时,会导致1~~n中出现空余位置，返回结果必然在1~n中，因此对于A中出现了小于等于0或大于n的值,可以不采取任何操作
② 经过以上分析可以得出算法流程:从A[0]开始遍历A,若0<A[i]<=n.则令B[A[i]-1]=1;否则不做操作。对A遍历结束后，开始遍历数组B，若能查找到第一个满足B[i]==0的下标i，返回i+1即为结果，此时说明A中未出现的最小正整数在1~n之间。若Bii]全部不为0，返回i+1（跳出循环时i=n，i+1等于n+1)，此时说明A中未出现的最小正整数是n+1
9. 定义三元组(a, b,c)(a、b、c均为正数）的距离D=a-b+|b-c+Ic - a。给定3个非空整数集合S、S2和S,按升序分别存储在3个数组中。请设计一个尽可能高效的算法，计算并输出所有可能的三元组(a, b,c) (aES,bES, cES）中的最小距离。例如S={H1, 0, 9}, S={-25,-10, 10,11}SJ={2,9,17, 30, 41}，则最小距离为2，相应的三元组为(9, 10, 9)
思想：
1. 设计一个递归算法，删除不带头结点的单链表L中所有值为×的结点
思想：
① 设f(L,x)的功能是删除以工为首结点指针的单链表中所有值等于x的结点，显然有f(L->next,x)的功能是删除以L->next为首结点指针的单链表中所有值等于x的结点。由此,可以推出递归模型如下。
（1) 终止条件:f(L,x)=不做任何事情; 若L为空表
（2) 递归主体:f(L, x)=删除*L结点;f(L->next, x); 若L->data==X
（3) :f(L,x)=f(L->next, x); 其他情况
2. 在带头结点的单链表L中，删除所有值为×的结点,并释放其空间假设值为×的结点不唯一，试编写算法以实现上述操作
思想：
① 采用尾插法建立单链表。用p指针扫描工的所有结点，当其值不为x时，将其链接到L之后，否则将其释放
3. 试编写算法将带头结点的单链表就地逆置，所谓“就地”是指辅助空间复杂度为O(1)
思想：
① 将头结点摘下，然后从第一结点开始，依次插入到头结点的后面(头插法建立单链表)，直到最后一个结点为止，这样就实现了链表的逆置
4. 给定两个单链表，编写算法找出两个链表的公共结点
思想：
① 先把问题简化:如何判断两个单向链表有没有公共结点?应注意到这样:一个事实:若两个链表有一个公共结点，则该公共结点之后的所有结点都是重合的，即它们的最后一个结点必然是重合的。因此，我们判断两个链表是不是有重合的部分时，只需要分别遍历两个链表到最后一个结点。若两个尾结点是:一样的，则说明它们有公共结点，否则两个链表没有公共结点。
② 然而，在上面的思路中，顺序遍历两个链表到尾结点时，并不能保证在两个链表上同时到达尾结点。这是因为两个链表长度不一定一样。但假设一个链表比另一个长k个结点，我们先在长的链表上遍历k个结点，之后再同步遍历，此时我们就能保证同时到达最后一个结点。由于两个链表从第一个公共结点开始到链表的尾结点，这一部分是重合的，因此它们肯足也是同时到达第一公共结点的。于是在遍历中，第一个相同的结点就是第一个公共的结点。
③ 根据这一思路中，我们先要分别遍历两个链表得到它们的长度，并求出两个长度之差。在长的链表上先遍历长度之差个结点之后，再同步遍历两个链表，直到找到相同的结点，或者一直到链表结束。此时，该方法的时间复杂度为 O(len1 + len2)
5. 已知两个链表A和B分别表示两个集合，其元素递增排列。编制函数、求A与B的交集，并存放于A链表中
思想：
① 算法思想:采用归并的思想,设置两个工作指针pa和pb,对两个链表进行归并扫描，只有同时出现在两集合中的元素才链接到结果表中且仅保留一个，其他的结点全部释放。当一个链表遍历完毕后，释放另一个表中剩下的全部结点（链表归并类型的试题在各学校历年真题中出现的频率很高）
6. 
思想：
① 问题的关键是设计一个尽可能高效的算法,通过链表的一次遍历，找到倒数第k个结点的位置。算法的基本设计思想是:定义两个指针变盘p和q，初始时均指向头结点的下一个结点(链表的第一个结点)p指针沿链表移动;当指针移动到第k个结点时，4指针开始与p指针同步移动;当指针移动到最后一个结点时，指针所指示结点为倒数第k个结点。以上过程对链表仅进行一遍扫描
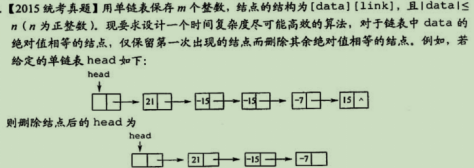
7. 
思想：
① 算法的核心思想是用空间换时间。使用辅助数组记录链表中已出现的数值，从而只需对链表进行一趟扫描。因为|datal≤n,故辅助数组q的大小为n+1，各元素的初值均为0。依次扫描链表中的各结点，同时检查q[ldatal]的值，若为0则保留该结点，并令q[ldatal]=1;否则将该结点从链表中删除
② 用哈希表：设长度为n+1的数组，每次插入一个元素因元素值与数组下标相同故在数组相应位置置为1，若检测为1则删除当前结点，反之为0插入且置为1
8. 设计一个算法完成以下功能:判断一个链表是否有环，如果有，找出环的入口点并返回,否则返回NULL
思想：
①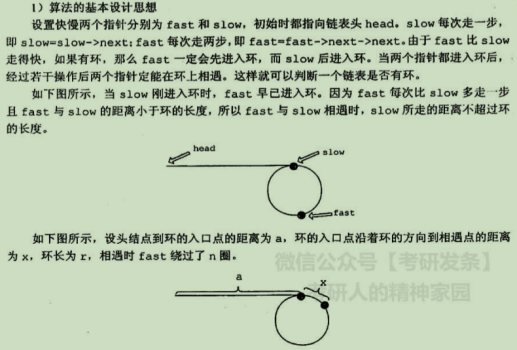 
（快慢指针也可作为求表长一半的方法)
9. 设线性表L=(a_1,a_2,…,a_(n-1),a_n)采用带头结点的单链表保存,链表中的结点定义如下:
typedef struct node
{int data;
struct node*next;
}NODE;
请设计一个空间复杂度为O(1)且时间上尽可能高效的算法，重新排列L中的各结点，得到线性表L'=(a_1,a_n,a_2,a_(n-1),a_3,a(n-2),…)
思想：
① 先观察L=(a_1,a_2,…,a_(n-1),a_n)和L'=(a_1,a_n,a_2,a_(n-1),a_3,a(n-2),…)，发现L'是由L摘取第一个元素，再摘取倒数第一个元素……依次合并而成的。为了方便链表后半段取元素，需要先将L后半段原地逆置[题目要求空间复杂度为O(1)，不能借助栈],否则每取最后一个结点都需要遍历一次链表
（1) 先找出链表L的中间结点，为此设置两个指针p和q,指针p每次走一步，指针q每次走两步,当指针q到达链尾时,指针p正好在链表的中间结点
（2) 然后将L的后半段结点原地逆置
（3) 从单链表前后两段中依次各取一个结点