限流,其基础含义为对流量进行限制,其既包括在速率上的限制,又包括在资源上的限制,这里主要讨论的是对速率进行限制。
本文分为三部分,第一部分中我们将讨论在做限流前必须要弄清的问题:
-
为什么要去做限流
-
限流的具体含义和指标
第二部分将具体探讨互联网上流行的限流算法;并在第三部分中学习它们在常用的限流中库中的高效实现,最后再简单的讨论下分布式限流的问题
阅读本文只需要基础的系统开发知识,可放心食用 : )
再谈限流
我们先来解决第一个问题,为什么我们要去做限流?
对于一台机器 (或一个服务) 来讲,它提供服务的能力必然存在某个阈值,这是由于其会被它本身的运算能力、内存、物理存储、网络资源与其所依赖的外部服务等因素所限制。而一旦超过了这个阈值,则必然无法对超出阈值的部分正常提供服务,故此时我们不得不做出一些策略来对这部分进行处理。
实际上,"一旦超过了这个阈值,则无法对超出的部分进行处理" 为一种较为乐观的预期。现实中超出阈值后,可能的情况还有对于其本来可以处理的、未超出阈值的部分,同样也无法进行处理,且最坏的情况甚至于导致机器宕机。
所以我们需要进行限流,且本文介绍的限流算法大多被应用在 OSI 模型的第七层中。
怎样去做限流的前置条件为弄清楚"限流"的定义。也就是说在去开启限流功能前,我们必须明白"限"是什么,"流"又是什么。
我们在讨论限流时一般将其解释为流量速率限制 (Rate Limit),即对于一段时间内超出指定通过阈值的流量进行控制,而根据控制方案的不同,又可分为:
- 拒绝式限流:对于超出阈值的流量,直接拒绝,返回失败。例如对于 HTTP 请求,可以直接返回 429 (Too Many Requests) ;如果在微服务中,则可能会启用降级策略。
- 阻塞式限流:对于超出阈值的流量,可以令它们阻塞或入队,使得这部分的请求阻塞等待,直到当前系统被使用的额度回归到阈值以下。
当我们选定了控制方案后,就确定了"限"字的含义。但"流"又是什么呢?换句话说,我们所限制的流量到底是什么?
被限制的"流"在不同的业务场景中有着不同的含义,如用户的发布贴子的速率、同时在线的房间人数、网盘的下载速率等。
而为了限制这些不同的"流",我们需要使用对应的流量指标来统计它们,其中我们可以使用 TPS (Transactions per second) 或 QPS (Queries per second) 作为指标以进行统计,前者为每秒事务数,后者为每秒查询数。而在"请求-响应"系统中,我们一般更倾向于使用 RPS (requests per second) 作为流量限制的指标。
为什么我们倾向于 RPS 而不是 TPS ?TPS 代表着每秒的事务数量,而事务含义为"一个实体执行的原子操作"(至少在逻辑上需要是原子的)。在业务上,我们当然希望知道一个完整业务操作的 TPS,但在业务的完成上由于用户行为的不可预知,一个事务完成的具体消耗时间很难被准确的测量。所以我们只好退而求其次,使用相对容易被监控且准确的 RPS。
除了 TPS、QPS、RPS 外,还有些其他常用的流量限制指标。例如在我们提到的"流"的限制业务场景中,除了第一个业务可以直接使用 RPS 作为流量限制指标外,第二个则需要以在线IP 作为指标、第三个需要以一段时间内的 TCP\UDP 的报文大小作为监控指标,根据不同的业务,你可以选择不同的限流算法来使用你选定的流量监控指标。
限流算法们
在确定好控制策略和流量监测指标后,接下来就可以讨论限流的基本策略了。
首先,我们先来思考一下怎么样的限流算法才算是一个好的限流算法,如果算法的好坏无法评判那么我们将无法挑选出最好的算法。
一个好的限流算法,又或者说流量控制算法,一方面必须做到保护资源,另一方面又应该做到在保证资源的使用在安全阈值内的同时,最大限度的利用资源。在计算机网络中有一个名词叫流量整形(Traffic Shaping),其含义是使部分数据报进行等待,使得流量曲线符合设定的流量配置。而我们需要的就是一条足够平稳的流量曲线,使得被保护的资源能够最大限度的被使用,也就是说能够对流量进行"削峰填谷"的算法是比较好的。
故我们理想中的流量曲线应该长下面这样:
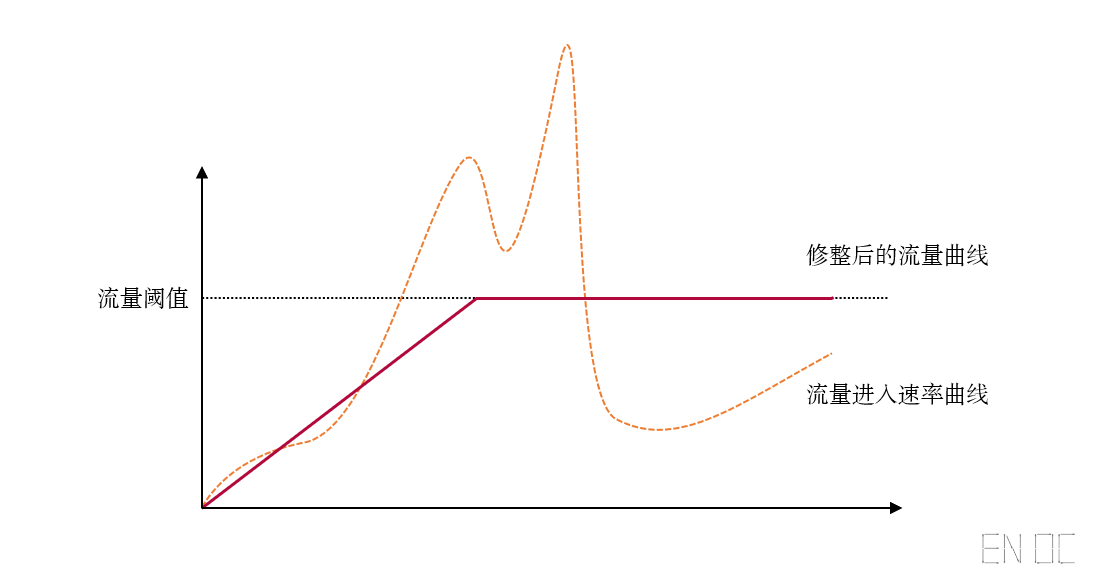
图中未到流量阈值前的部分为预热曲线,后面会进行详细介绍
计数窗口算法
我们先从最容易想到的思路开始:由于我们需要限制每秒的请求量,所以只需要统计每一秒收到的请求数量,超过则抛出异常。
用代码表示如下:
public void enter() {
long now = System.currentTimeMillis() % 1000;
if (lastTime != now) {
lastTime = now;
currentReq = 0;
}
if (currentReq < maxReq) {
currentReq++;
} else {
throw new RuntimeException("resource out!");
}
}
上述代码仅用于阐明算法思路,并没有考虑并发问题,实际实现中由于需要考虑各种低锁或无锁的并发方案,故大概率会与使用代码存在差别
这个算法足够简单,但也存在一些缺点:
-
只支持拒绝式限流
在我们对于限流算法的"削峰填谷"的要求中,这里已经实现了削峰,但填谷只是交给了服务的调用方简单的进行重试,不能很好的修整流量曲线。
-
有超出规定并发量的可能
这个缺点乍一看没什么可能出现,但仔细一想便会发现,我们对于一秒的定义存在问题,比如当前的下半秒 (500ms-1000ms) 和下一秒的上半秒 (1000ms-1500ms) 也能够被称为是一秒。而在该算法中是有可能出现例如 500ms-1000ms 有 80 个请求,1000ms - 1500ms 有 90 个请求,总请求量超过限制的一秒 100 的请求数的。
第一个缺点还好,但第二个就看起来有点难以容忍了,我们先来着手解决第二个问题。首先来考虑第二个问题产生的原因在哪,该算法之所以会超出限制,最直接的原因在于没有统计"整个秒",例如我们在 1200ms 中进入的请求,只考虑了 1000ms-1200ms 之间的请求,而实际上我们应该考虑 200ms-1200ms之间的请求,所以我们接下来要做的就是将缺少的那部分的请求也统计进去。
滑动日志算法
现在,我们为了将一秒内所有的请求都考虑在内,需要创建一个集合,来存储所有进入的请求的时间戳,集合的最大大小为允许通过的最大请求数量,一旦发现集合为满,则清理所有集合内小于 (当前时间戳 - 时间窗口大小) 的值。
简易动画演示如下:

在实际开发中,我们可以使用红黑树或跳表等结构来作为这个集合,这样在移除时就不需要线性扫描集合中所有元素。以下为简易的代码表示:
private void enter() {
long now = System.currentTimeMillis();
int currentReq = redBlackTree.size();
if (currentReq >= maxReq) {
redBlackTree.headSet(now - windowSize).clear();
currentReq = redBlackTree.size();
if (currentReq >= maxReq) {
throw new RuntimeException("resource out!");
}
}
redBlackTree.add(now);
}
这个方案很好的解决了在时间区间中时间点不连续的问题,但随即也带来了新的问题。一个最显而易见的缺点就是我们需要存储所有集合内的请求的时间戳,如果集合较大的话消耗的内存也会比较大。且另一方面,过期的时间我们还需要从集合中进行移除,而其中移除一个元素的时间复杂度最少为 \(O(logN)\) ,所以性能消耗也是比较大的。
这样看来上面这个方案在生产中并不可行,不过也给我们带来了一定的启发:
-
使用滑动窗口的思想
在上面中我们维护了一个窗口来存储所有的元素,窗口的思想本身并没有问题,但问题在于我们不应该存储所有的元素,因为这导致了集合元素过多和窗口移动效率低的问题,或许我们可以使用桶的思想来解决存储全部元素所带来的问题。
-
使用恰到好处的精度
在上面中我们可以使用任意精度的时间戳来控制并发量,只要你愿意甚至可以使用纳秒的精度。但我们真的需要这么高的精度吗?
实际上对于限制比较"软"的资源来讲,较高的精度带来受益并不高。对于这些应用,我们完全可以适当的放弃一些精度,使得少量请求被错误的允许或拒绝,带来的影响并不会很高,但却可以获得不错的收益。
带着以上两点思考,我们再来重新设计限流算法。
滑动窗口算法
首先根据桶的思路,我们可以维护多个桶,桶的精度可以适当的降低,例如每 100ms 一个桶。同时维护窗口内的所有桶的统计值,当时间推进,统计值减去从窗口左侧丢弃的桶,一旦当前的统计值超过限制值,则可拒绝请求。
流程示例:
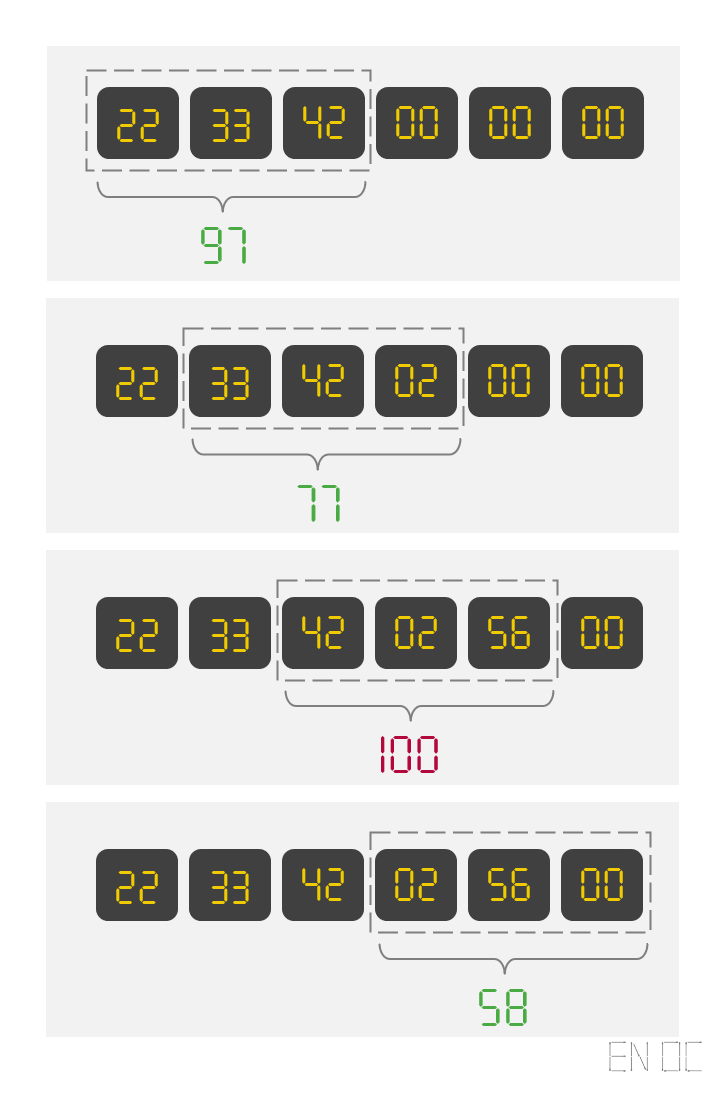
简易代码表示:
public boolean enter(int count) {
long now = System.currentTimeMillis();
syncWindow(now);
if (passSum + count > windowMaxPass) {
return false;
}
window[currentIdx] += count;
passSum += count;
return true;
}
private void syncWindow(long now) {
// 求出每个桶的大小
final int bucketSize = this.windowSize / this.window.length;
// 窗口需要移动的格数
int step = (int) ((now - currentTime) / bucketSize);
if (step == 0) {
return;
}
// 右指针需要移动到的位置
int nextIdx = (currentIdx + step) % window.length;
// 如果超过窗口大小, 可以直接清空窗口
if (step >= window.length) {
Arrays.fill(window, 0);
passSum = 0;
} else {
// 否则向前移动到指定的位置
while (currentIdx != nextIdx) {
currentIdx = (currentIdx + 1) % window.length;
passSum -= window[currentIdx];
window[currentIdx] = 0;
}
}
// 最后更新时间
this.currentTime = now;
}
当然,这个算法仍然是存在着误差的,它仍然会存在着在计数窗口算法中的超出限额的问题。不过由于在图片示例中我们将精度设置为了 100ms,此时超出限额的概率与大小已经缩小了不少,当然你也可以使用更小的桶以获得更高的准确度。
改进的计数窗口算法
我们还可以换个思路,既然我们不需要太高的精度,那么我们可以直接从计数窗口的方案中进行改进。
如果我们的窗口大小为 1s ,则可以直接存放上一秒的统计值和当前秒的统计值,然后根据当前秒内的毫秒进行计算:
\[\begin{equation} \begin{aligned} avg\_count=\ &last\_secord\_request\_count\ * \\ &(1000-current\_mill)/1000+current\_secord\_request\_count \end{aligned} \end{equation} \]当然由于我们的采样为基于上一个采样周期的平均值,所以实际上得到的只是实际速率的近似值。不过根据 Cloudflare 的分析报告 ,实际环境中四亿个请求中只有 0.003% 的请求被错误的允许或拒绝,并且该方案的内存占用与实际运行效率都很不错,所以确实也可以作为一个良好的限流算法。
如果只需要简单的限流,以上算法已经足够满足我们的需要了,但是我们限流的目的,除了保护资源外,还需要起到"削峰填谷"的作用,我们目前的算法对于超出额度的流量只能进行简单的拒绝,而对于"填谷"则依赖于调用方的重试操作,这样的话就很难依据我们自己的需要去调整流量曲线,实际上这也是拒绝式限流的缺点。
如图,曲线并没有想象中的平滑,这是因为重试的时间受网络状况所影响而变得难以预测:
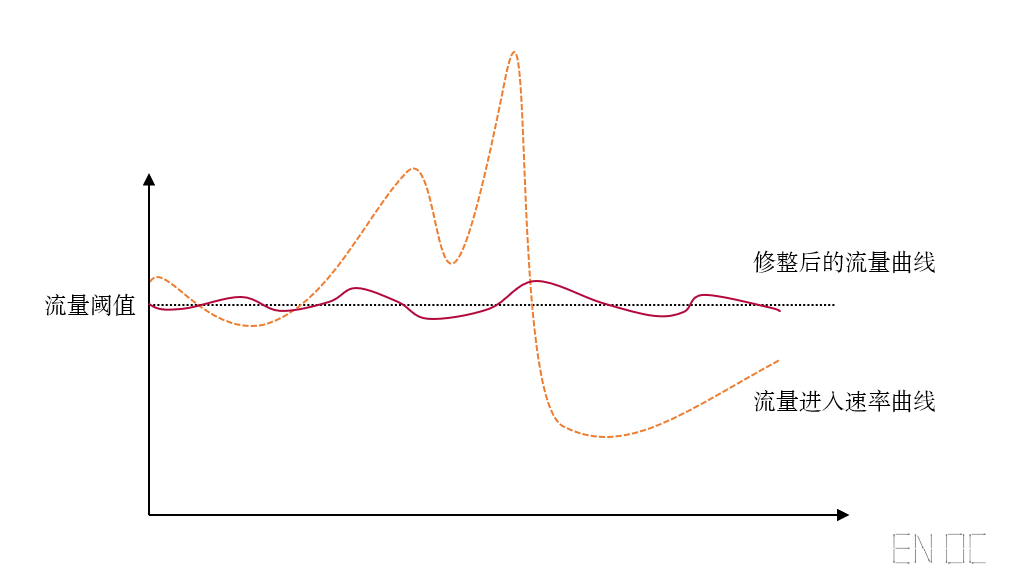
从根本上讲,出现这样的情况是因为我们目前的算法都只能进行拒绝式限流,而想要修整出更加平滑的曲线则需要阻塞式限流来自定义等待时间,所以我们还需要寻找其他的出路。
漏桶算法
想象一个我们有一个用于装水的桶,桶的底部有一个洞,水会以恒定速率从洞中流出,同时我们还会往桶中注入水,而当注入水的速度大于水流出的速度,桶中的水将会很快的超过桶的容量,然后溢出。
在漏桶算法中,"水"就是进来的请求流量,"从洞中漏出"就是服务处理请求,"桶"即为存放等待被处理的请求的集合,同时"水从桶中溢出"则代表超过了最大的容量后执行拒绝策略。
这个算法原理和实现都比较简单,我们用一个 FIFO 队列来存放进来的请求,服务在另一端以恒定的速率处理请求,队列满则丢弃新进来的请求。
这个算法看起来挺美好,能够简单的实现等待策略,并且通过恒定的速率流量曲线能够轻易的被修整为较直的曲线,但仍具有几个缺点:
-
大流量时会使队列被旧请求所填满,若此时处理的不够及时会导致最近的请求不能被处理。
不过这个缺点我们可以通过给桶中的请求添加 TTL 等方式来做处理。
-
该算法有"桶的大小"和"流出速率"两个参数,但合理的设置它们是有一定难度的,对于桶的大小,过大或过小都会存在着问题。
令牌桶算法
幸运的是我们确实有一个更完美的算法来替代它,同时这也是在限流算法中最为常见的算法,实际上大多数限流库都是使用的该算法。
想象我们具有一个装令牌的桶,当请求到来时会尝试从桶中获取一个令牌,如果为空则被拒绝或阻塞等待;同时每过段时间就往里面扔令牌,但桶满时令牌就会溢出丢弃。
你可以在信号量的基础上理解令牌桶算法,当进入的时候会使用 \(\text P\) 操作减少值,一但值为零直接拒绝或阻塞,不过区别在于离开时不会调用 \(\text V\) ,而是定时的调用 \(\text V\) ,且信号量的值到达一个上限后不会再增加。
该算法的优点在于简单且高效,放入令牌的速率可以简单的根据具体情况控制,并且性能消耗较少,因为你并不需要真的设置一个线程去定时的放入令牌,只需要根据上次放入的时间戳进行对比即可,所以实际上的消耗也就几个变量的维护。
以下为简易实现(带并发):
public class TokenBucketRateLimiter {
private final AtomicInteger tokenCount;
private final AtomicLong lastAddedTime;
private int bucketSize;
private double rate;
private int minimumWaitingTime = 10;
public TokenBucketRateLimiter(int maxToken, double rate) {
this.bucketSize = maxToken;
this.tokenCount = new AtomicInteger(maxToken);
this.lastAddedTime = new AtomicLong(System.currentTimeMillis());
this.rate = rate;
}
public int get(int accept) {
int c = tokenCount.get();
int wait = 0;
boolean gain = false;
addAndGetTokens: while (!gain) {
for (;;) {
long now = System.currentTimeMillis();
long latest = lastAddedTime.get();
double rate = this.rate;
// 上一次添加 Token 的时间到当前时间的间隔
int interval = (int) (now - latest);
// 该间隔所能添加的 Token 的数量
int except = (int) (interval / 1000 * rate);
if (except > 0) /* 如果能添加的 Token 大于 0, 则允许添加 */ {
// 通过 CAS 更改时间, 如果能够成功说明获得了添加 Token 的权利
if (lastAddedTime.compareAndSet(latest, now)) {
int sc;
do {
c = tokenCount.get();
// 保证添加后的 Token 数量不会超过上限
sc = Math.min(bucketSize, c + except);
} while (!tokenCount.compareAndSet(c, sc));
// 添加完成后, 继续执行 Token 获取的流程
break;
} else {
Thread.onSpinWait();
}
} else if (c >= accept) /* 如果剩余的 Token 数量足够且无需添加, 也可进入下一步 */ {
break;
} else /* 否则直接返回等待指定数量的 Token 所需要的时间(ms) */ {
wait = (int) Math.ceil(1000 / rate) * accept - interval;
break addAndGetTokens;
}
}
do {
c = tokenCount.get();
} while (c > 0 && !(gain = tokenCount.compareAndSet(c, c - 1)));
}
return wait;
}
}
限流库的实现
在了解完现在在网络上流行的主流限流算法后,我们再来看一下在实际时的限流库的实现,其中由于很多限流库用到了各种无锁策略和专门做了对"伪共享"、惊群效应等常见并发问题的处理,所以你可能会对它们稍微有点陌生。我们先来看最流行的在 Guava 中的限流算法的实现。
Guava 实现
Guava 的限流算法使用的是令牌桶算法,且支持预热功能,使用也十分简单。
基础用例// 创建一个限流器, 其中每秒对桶中放入 1000 个令牌
RateLimiter limiter = RateLimiter.create(1000);
// 同上, 但预热时间为 1s
RateLimiter limiterWithWarmup = RateLimiter.create(1000, Duration.ofSeconds(1));
if (!limiter.tryAcquire(1)) {
throw new RuntimeException("too fast!");
}
// 我们将等待 1 个令牌可用
limiter.acquire(1);
普通模式实现
我们先来分析普通模式下的实现
public double acquire(int permits) {
// 计算获取指定 permit 所需要等待的时间
long microsToWait = reserve(permits);
// 等待指定时间
stopwatch.sleepMicrosUninterruptibly(microsToWait);
// 返回等待的时间
return 1.0 * microsToWait / SECONDS.toMicros(1L);
}
其中主要观察 reserve 方法
final long reserve(int permits) {
checkPermits(permits);
synchronized (mutex()) /* 获得互斥锁进行加锁 */ {
return reserveAndGetWaitLength(permits, stopwatch.readMicros());
}
}
这里使用的是对一个 Object 对象使用 synchronized 的方式进行加锁,接下来看具体代码:
这段代码的入参为需要获取的 permit 数量与当前时间,同时返回需要等待的时间
final long reserveEarliestAvailable(int requiredPermits, long nowMicros) {
// 首先填充 permit 的数量
resync(nowMicros);
long returnValue = nextFreeTicketMicros;
// 计算将要消耗的 permit 的数量
double storedPermitsToSpend = min(requiredPermits, this.storedPermits);
// 还需要的 permit 的数量
double freshPermits = requiredPermits - storedPermitsToSpend;
long waitMicros =
// (预热模式下启用, 否则为 0)
storedPermitsToWaitTime(this.storedPermits, storedPermitsToSpend)
// 需要的 permit 数量 * 获取单个 permit 所需时间
+ (long) (freshPermits * stableIntervalMicros);
// 将上次添加 permit 的时间加上需要等待的时间(相当于预支了这部分的 permit, 之后会 sleep 这段预支的时间)
this.nextFreeTicketMicros = LongMath.saturatedAdd(nextFreeTicketMicros, waitMicros);
// 减去消耗的 permit 数量
this.storedPermits -= storedPermitsToSpend;
return returnValue;
}
其中 resync 方法是在进行获取令牌前根据当前的时间和上次添加时间进行回填
void resync(long nowMicros) {
// 如果当前时间大于下一次能够 permit 的时间, 则进行获取
if (nowMicros > nextFreeTicketMicros) {
// 计算能够添加的 permit 数量 (现在与上一次获取的时间的间隔 / 生成一个令牌所需的时间)
double newPermits = (nowMicros - nextFreeTicketMicros) / coolDownIntervalMicros();
// 保证 permit 存储数量小于上限的情况下进行增加
storedPermits = min(maxPermits, storedPermits + newPermits);
// 在添加 permit 后更新时间
nextFreeTicketMicros = nowMicros;
}
}
同时在设置新的 rate 的时候会令当前存储的 permit 比例放大或缩小
storedPermits =
(oldMaxPermits == 0.0)
? 0.0 // initial state
: storedPermits * maxPermits / oldMaxPermits;
预热功能
Guava 的 RateLimiter 还包含预热功能,我们可以在初始化的时候设置预热时间参数,这适用于资源需要预热的场景。例如缓存池,在开始时或很久没有请求时缓存池是空的,此时如果忽然有大量请求打过来,则由于缓存池为空,则大量请求会打到数据库,导致数据库可能发生宕机;而如果此时直接使用限流功能,若允许通过的流量过小,则导致缓存池在填充完成后能够处理的请求大于一开始允许通过的请求量。那么此时如果使用预热功能,使得资源在预热阶段加载到缓存,在预热完成后允许更高的流量通过,则可以最大限度的"压榨"服务的性能。
我们来看预热功能具体的实现原理:
以下为展示预热功能的一张图,其 \(X\) 轴表示的是桶中存放的令牌数量,\(Y\) 轴为从桶中取出一个令牌所需要花费的时间:
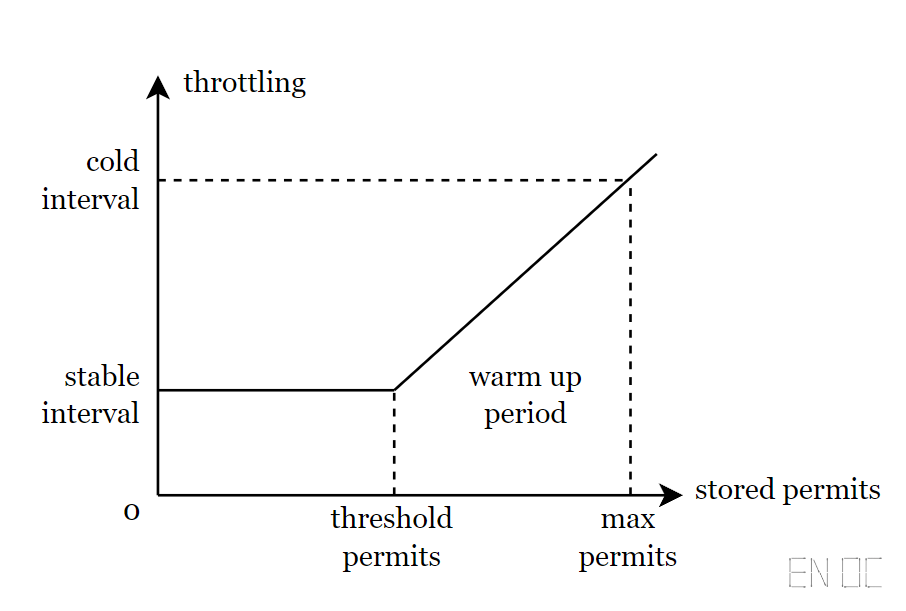
从图中我们可以看出,当令牌桶满的时候,即 permit 数量等于 \(max\_permits\) 时,此时所需要花费的时间是最多的,为 \(cold\_ interval\) ;然后我们不断的从桶中取出令牌,此时所花费的时间越来越少,直到桶中令牌数小于 \(threshold\_permits\) ,此时取出一个令牌所需的时间将固定为 \(stable\_interval\)。
你可以发现,当令牌桶满时,此时一般为较长时间没有获取资源,而此时如果需要获取则要进行"预热",我们在该算法中刚好会等待较长时间,这正好符合了我们的需求!所以该算法确实可以作为预热功能的实现。
简单的了解了实现原理后,我们接下来学习该算法的具体细节(别担心,只需要初中数学水平
