神经网络由多个神经元组成,其中神经元由几个部分组成:输入、输入权重、输出和激活函数组成,类似于生物神经元的树突、轴突的组成。
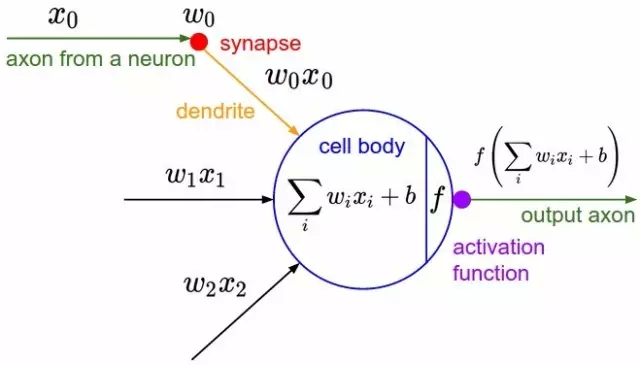
神经元的输入由左边的神经元输出 \(x\) 乘以权重 \(w\) 并加和得到,输出的时候,类似于生物神经元的轴突,将神经元的输出通过激活函数才能传送给接下来的神经元。
常用的激活函数(activation function)是Sigmod,它的函数图像如下,在逻辑回归的时候使用过:
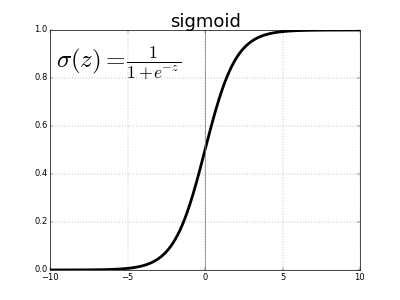
其中偏置单元 \(b\) 是用于提高神经网络的灵活性而加入的,它的存在可以让激活函数更快或者更慢达到激活状态。
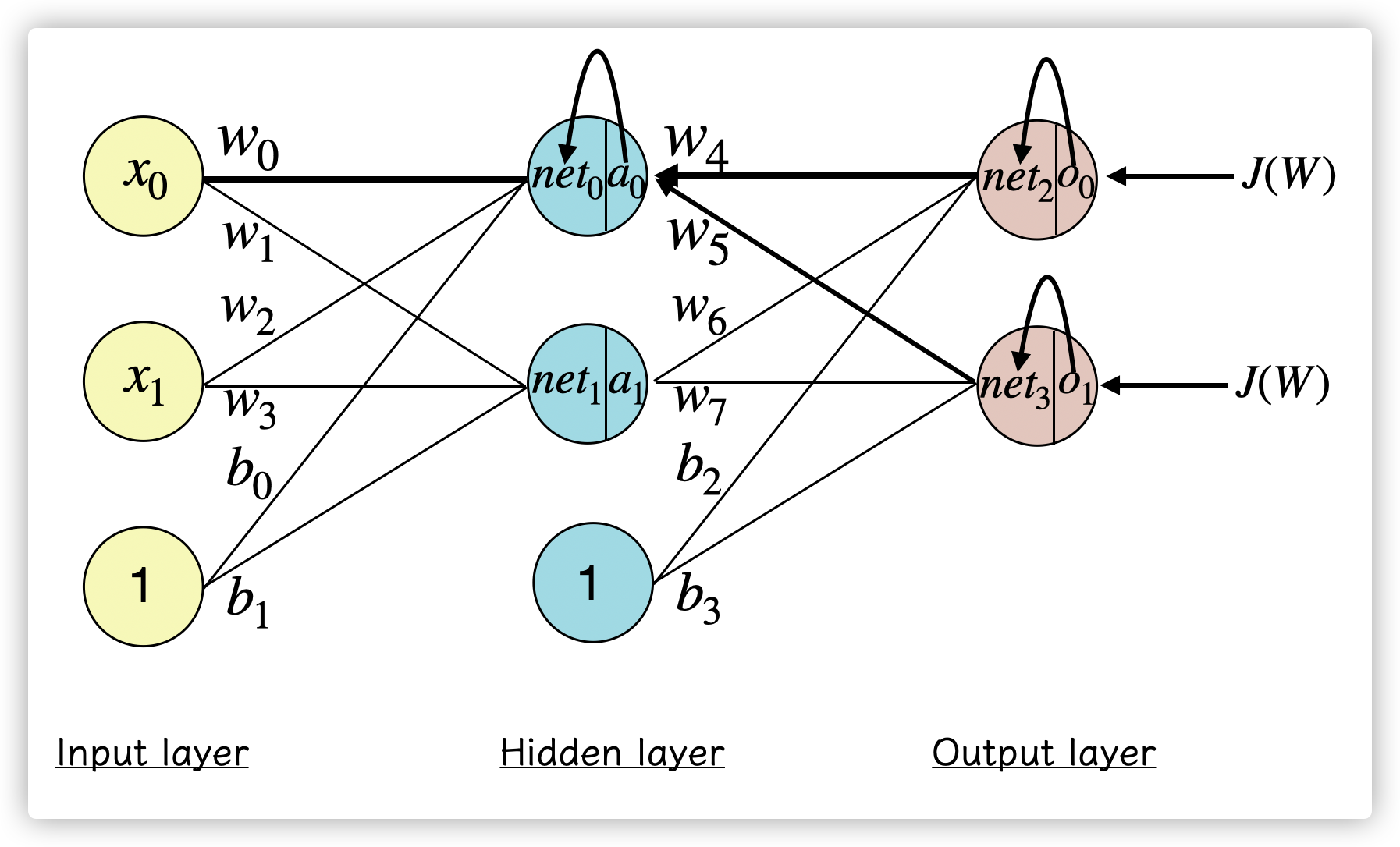
神经网络多个神经元组层一个神经网络:
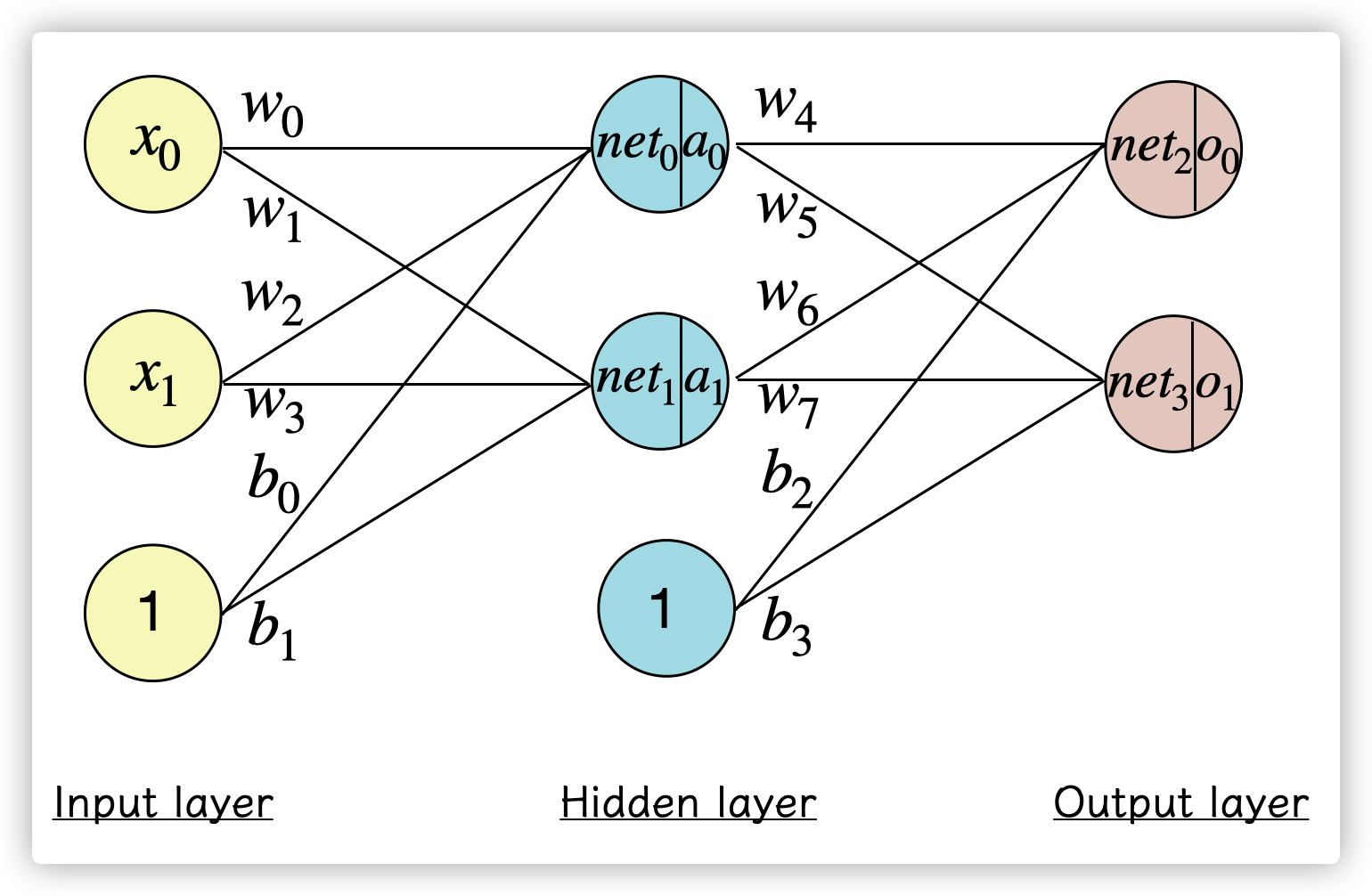
神经网络第一层是输入层(input),最后一层是输出层(output),而中间的就是神经网络的隐藏层(hidden layer)
神经网络的训练过程如下:
- 随机初始化权重 \(w_i\)
- 代入执行前向传播得到神经网络的输出 \(o_i\)
- 计算代价函数 \(J(W)\)
- 执行反向传播,计算偏导数 \(\frac{\partial J(W)}{\partial w_i}\) ,依次更新网络的权重
- 将样本 \((x_i,y_i)\) 不断代入第2步到第4步。
前向传播的过程目的是计算出神经网络的输出:
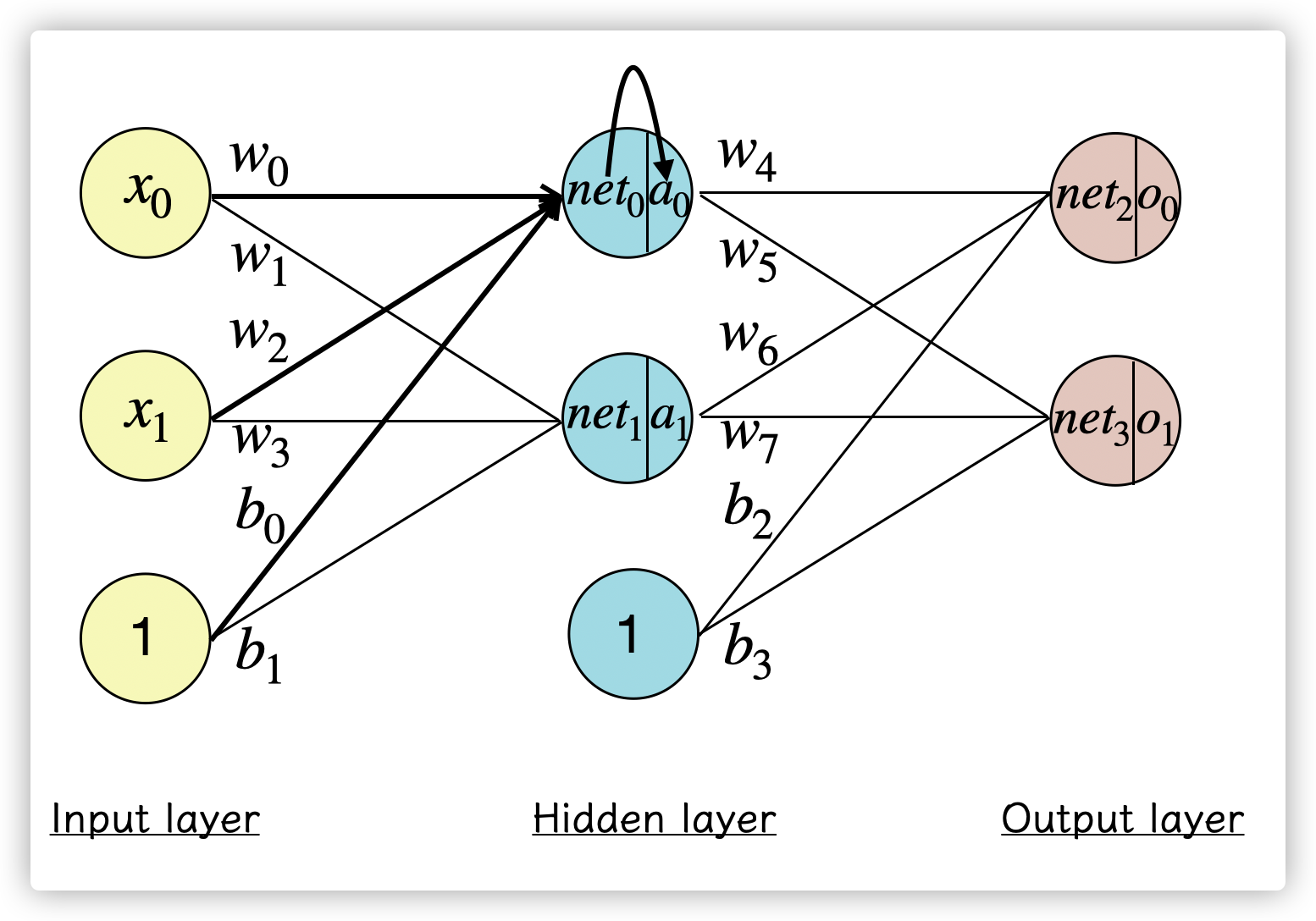
首先开始计算 \(net_0\) :
\[net_0 = w_0 * x_0 + w_2 * x_1 + b_0 * 1 \]到达隐藏层的神经元后,会通过激活函数作为神经元的输出 \(a_0\):
\[a_0 = Sigmoid(net_0) = \frac{1}{1-e^{-net_0}} \]计算该神经元后继续向前计算,和前面一层的计算类似:
\[ o_0 = Sigmoid(w_4 * a_0 + w_6 * a_1 + b_2 * 1) \]按照这样的传播过程,这样就能计算出神经网络的输出 \(o_1,o_2,\dots,o_n\) ,即神经网络的前向传播,就像把样本 \(x\) 代入\(y = ax + b\)里求出 \(y\) 值的过程一样。
反向传播按照神经网络的训练过程,接下来是希望计算代价函数 \(J(W)\) ,并求出 \(J(W)\) 对 \(w_i\) 的偏导数 \(\frac{\partial J(W)}{\partial w_i}\) ,并按照学习率 \(a\) 更新参数:
\[w_i = w_i - a * \frac{\partial J(W)}{\partial w_i} \]以更新 \(w_5\) 为例,如果需要知道 \(\frac{\partial J(W)}{\partial w_5}\) 的值,根据链式求导法则:
\[\frac{\partial J(W)}{\partial w_5} = \frac{\partial J(W)}{\partial o_1 } * \frac{\partial o_1}{\partial net_3} * \frac{\partial net_3}{\partial w_5} \]
(1)首先求\(\frac{\partial J(W)}{\partial o_1 }\) ,其中 \(J(W)\) 是代价函数,这里用均方误差来计算误差,\(y\) 是样本的结果,那么表达式就是:
\[J(W) = \frac{1}{2}\sum_{i=1}^{m}(y_i - o_i)^2 = \frac{1}{2}(y_0 - o_0)^2 + \frac{1}{2}(y_1 - o_1)^2 \]其中对 \(o_1\) 的偏导数为:
\[\frac{\partial J(W)}{\partial o_1 } = 0 + 2 * \frac{1}{2} (y_1 - o_1) * -1 = -(y_1 - o_1) \](2)然后是求 \(\frac{\partial o_1}{\partial net_3}\):
\[o_1 = Sigmoid(net_3) \]其中对 \(net_3\) 的偏导数为:
\[\frac{\partial o_1}{\partial net_3} = Sigmoid(net_3)' = Sigmoid (net_3) * (1 - Sigmoid(net_3) \]激活函数Sigmoid的函数 \(f(x)\) 的导数等于 \(f(x)*(1-f(x))\) ,见证明。
(3)最后是求 \(\frac{\partial net_3}{\partial w_5}\) :
\[net_3 = w_5 * a_0 + w_7 * a_1 + b_1 \]\[\frac{\partial net_3}{\partial w_5} = a_0 * 1 + 0 = a_0 \]所以最终求得偏导项:
\[\frac{\partial J(W)}{\partial w_5} = -(y_1 - o_1) * Sigmoid (net_3) * (1 - Sigmoid(net_3)) * a_0 \]而 \(w_5\) 也能在反向传播中更新自己的权重,通过减去 \(a * \frac{\partial J(W)}{\partial w_5}\)。
第三个导数项求偏导时都会等于上一层的激活函数的输出值,如果把前两个导数项 \(\frac{\partial J(W)}{\partial o_i } * \frac{\partial o_i}{\partial net_i}\) 用符号 \(\delta_i\) 代替的话,那么:$$\frac{\partial J(W)}{\partial w_5} = a_j\delta_i$$
如果要更新隐藏层的权重 \(w_1\) ,则
\[\frac{\partial J(W)}{\partial w_1} = \frac{\partial J(W)}{\partial a_0 } * \frac{\partial a_0}{\partial net_0} * \frac{\partial net_0}{\partial w_1} \]因为 \(\frac{\partial J(W)}{\partial a_0 }\) 同时受到 \(o_0\) 和 \(o_1\) 的影响,所以:
\[\frac{\partial J(W)}{\partial w_1} = (\frac{\partial J(W)_0}{\partial a_0 } + \frac{\partial J(W)_2}{\partial a_0 }) * \frac{\partial a_0}{\partial net_0} * \frac{\partial net_0}{\partial w_1} \]其中 \(J(W)_0\) 代表在 \(o_0\) 的损失,计算和前面的规则类似,依次根据链式求导规则展开即可对给定的 \((x_i, y_i)\) 拟合。
其他资料在这里基本打开了神经网络的大门,虽然目前学到只是一个全连接网络和基本的BP算法,但是在这篇文章中可以看到还有支持增量学习的自适应谐振理论网络(ART),以及自动连接神经元的自我组织网络(SOM)等等网络架构。
其他我用到的资料:
- 一步一步进行反向传播: https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
- 上文的在 cnblog 中文翻译: https://www.cnblogs.com/charlotte77/p/5629865.html
- Sigmoid 激活函数求导推导: https://zhuanlan.zhihu.com/p/215323317
- bias 的作用: https://www.zhihu.com/question/305340182
