上一篇讲到最早的计算机是什么样的,有人可能会不服气,咱们中国的算盘才应该是计算机的祖宗才是啊。算盘应该算得上是一种计算工具,可以类比到现代计算机的存储,真正做运算的实际上还是人脑。最早的计算机实际上只能做一些简单的加减乘除运算,只能叫计算器,跟现在的计算机(俗称电脑)还差的很远。但是,今天说到的差分机比前面讲到的就更接近现代计算机了。
差分机的诞生从17世纪到20世纪,计算器从手摇演变成了电动。但是整整三百年期间,计算器仍只能做最简单的四则运算,需要人力不断的记录计算结果,然后做下一步的运算。这种繁琐的人工操作能不能也交给机器来完成呢?第一个用实际行动验证这一想法的,是来自英国的旷世奇才——查尔斯·巴贝奇(Charles Babbage)。
差分机的设想,最早由一位名为约翰·赫尔弗里奇·冯·米勒(Johann Helfrich von Müller)的德国工程师在1784年提出,但他没有得到资金支持。
18世纪末,法兰西发起了一项宏大的计算工程——人工编制《数学用表》,这在没有先进计算工具的当时,是件极其艰巨的工作。法国数学界调集大批数学家,组成了人工手算的流水线,算得天昏地暗,才完成了17卷大部头书稿。即便如此,计算出的数学用表仍然存在大量错误。
巴贝奇在他的自传《一个哲学家的生命历程》里,写到了大约发生在1812年的一件事:
有一天晚上,我坐在剑桥大学的分析学会办公室里,神志恍惚地低头看着面前打开的一张对数表。一位会员走进屋来,瞧见我的样子,忙喊道:"喂!你梦见什么啦?" 我指着对数表回答说:"我正在考虑这些表也许能用机器来计算!"
巴贝奇耗费了整整十年光阴,于1822年完成了第一台差分机,它可以处理3个不同的5位数,计算精度达到6位小数,当即就演算出好几种函数表。第二台由英国政府出资的运算精度为20位的大型差分机差分机一号(Difference Engine No.1)由于当时的制造工艺落后等问题最终未能完成。1849年巴贝奇提出支持31位、7次差分的差分机2号(Difference Engine No.2)方案,却在有生之年只实现了很小一部分。
为什么叫差分机差分机这个名字,源自其所使用的算法,是帕斯卡在1654年提出的差分思想:n次多项式的n次数值差分为同一常数。
我们来看一个一次多项式的例子,其中 Δƒ(x) = ƒ(x+1) - ƒ(x)

我们再来看一个二次多项式的例子,其中 Δ1ƒ(x) = ƒ(x+1) - ƒ(x),Δkƒ(x) = Δk-1ƒ(x+1) - Δk-1ƒ(x)
具体证明过程我也没能找到,大学学的数学都还给老师了。。。有知道证明过程的可以在评论区告诉我。
利用差分的方法,可以轻易把复杂高阶多项式的值通过重复进行加减法来计算。下面以一个二次多项式为例:
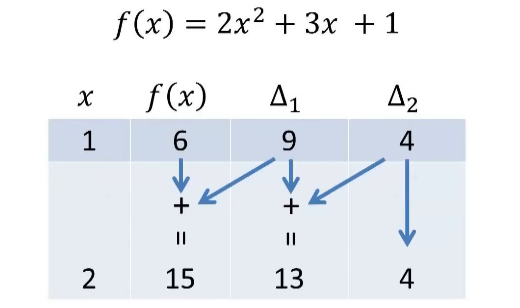
首先人工计算出 ƒ(1)、 Δ1ƒ(1)和 Δ2ƒ(1)的值,根据定义,有:
ƒ(2) = ƒ(1) + Δ1ƒ(1) , Δ1ƒ(2) = Δ1ƒ(1) + Δ2ƒ(1) , Δ2ƒ(2) = Δ1ƒ(2)
ƒ(3) = ƒ(2) + Δ1ƒ(2) , Δ1ƒ(3) = Δ1ƒ(2) + Δ2ƒ(2) , Δ2ƒ(3) = Δ1ƒ(2)
ƒ(4) = ƒ(3) + Δ1ƒ(3) , Δ1ƒ(4) = Δ1ƒ(3) + Δ2ƒ(3) , Δ2ƒ(4) = Δ1ƒ(3)
...
以此类推,可以不断地计算出后面的ƒ(x)的值。同理,更高阶的多项式也可以通过类似的方式求得:
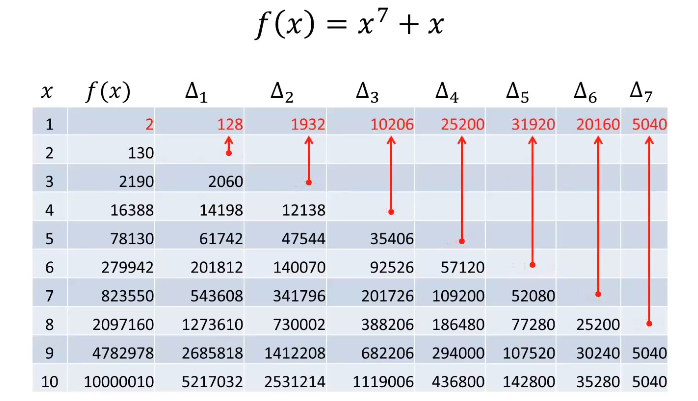
要使用差分法来计算多项式,那么机器必须能够完成以下功能:
- 输入并保存ƒ(1)、Δ1ƒ(1)、Δ2ƒ(1)、Δ3ƒ(1) ...
- 计算 ƒ(k) + Δ1ƒ(k)、Δ1ƒ(k) + Δ2ƒ(k)、Δ2ƒ(k) + Δ3ƒ(k) 并保存和输出结果
- k = k+1 , 重复第二步

差分机通过一系列同轴齿轮来存储数字,每个齿轮可以存储10个数,最高可以存储31位的十进制数。
差分机最多可以存储8个数,最高能计算7次方的多项式
计算 并行化算法跟早期的计算器类似,差分机也是通过齿轮的转动进行加减法。巴贝奇先把串行的计算流程并行化。未优化的差分法每次运算只能计算一次加法,对于7阶计算需要运算7步才能得到结果
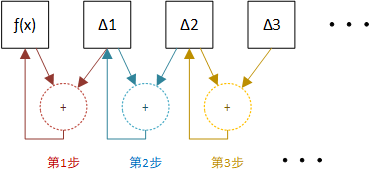
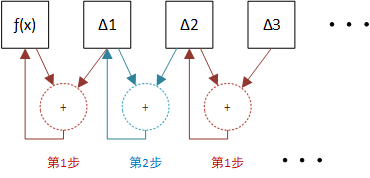
对于机械设计而言,串行控制远比并行控制成本更高,因为下一个运算必须要等待上一个运算结束,巴贝奇通过并行化将7步简化成了2步:
首先,简化后的步骤需要人工计算更多的数字,这对于提升的性能而言显然是值得的,下面以7阶计算为例:

第一步,将第1个数和第2个数、第3个数和第4个数、第5个数和第6个数、第7个数和第8个数相加:
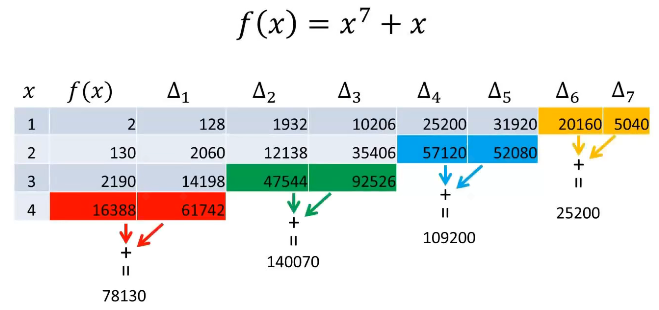
第一步计算结束后更新第1、3、5、7个数:
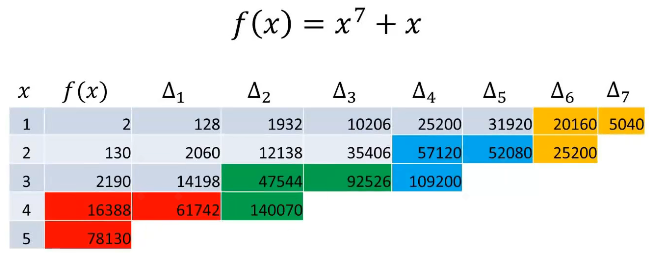
第二步,将第2个数和第3个数、第4个数和第5个数、第6个数和第7个数相加:
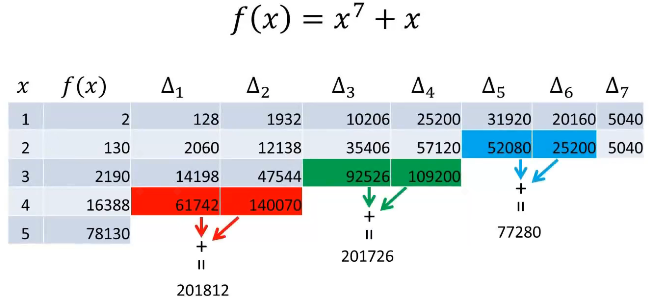
第二步结束后,更新第2、4、6个数:
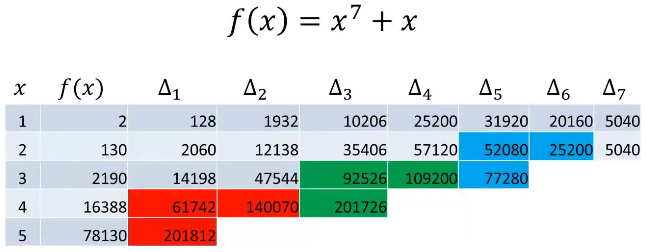
继续上述两个步骤,就可以源源不断地计算出ƒ(x)的值。
整个流程看起来是这样的,值得注意的是,现在这几个存储里面的x值并不相同,但是这并不影响计算。

每个齿轮都有4组从0到9的数字,每个0跟9的交界处会有一个突起用来提醒进位

进位装置
进位这里不进行细述,有兴趣的可以通过引用里的链接了解更多。

两个齿轮可以简单完成加法操作,只需要先分开两个齿轮,把第二个齿轮转到到需要加的值,合拢两个齿轮,顺时针转动第二个齿轮转到0,第一个齿轮就会自动加上第二个齿轮的数字。
但是这个方法有个问题,转动后第二个齿轮的数字就已经丢失了,所以巴贝奇在中间加了第三个扇形轮:

这个扇形轮有三种模式:咬合两个齿轮、只咬合第二个齿轮和两个齿轮都不咬合。在进行累加时,扇形轮与两个齿轮咬合,在转动第二个齿轮的时候会带动第一个齿轮进行累加;完成运算后,扇形轮抬起只与第二个齿轮咬合,带动第二个齿轮恢复到原来的数字。
因为篇幅有限,本文先讲到这里,感兴趣的可以通过后面的链接来了解更多。最后,大家可以通过这个视频来感受一下差分机的精妙:https://www.bilibili.com/video/BV1MW41177yh/?spm_id_from=autoNext。在下一篇,我们将会进入电气时代,了解下真正的现代电子计算机。
引用:
https://xueqiu.com/3993902801/81799392
https://zhuanlan.zhihu.com/p/107462919
https://www.bilibili.com/video/BV1rt4y1S77M?spm_id_from=333.999.0.0
https://www.bilibili.com/video/BV1mt411C7gw?p=1
https://zh.wikipedia.org/wiki/%E5%B7%AE%E5%88%86%E6%A9%9F
