有限体积法求解一维非稳态对流扩散方程

介绍一维非稳态对流扩散方程的离散求解方法 1. 源起

最近想用有限差分法计算二维的顶盖驱动流，在推导过程中遇到了许多问题，例如对流项的离散、“线性化”这一在有限体积法中很常见的操作、\(1-\delta\)压差在有限差分法中的实现、压力项的离散等等。以上问题让我感觉自己理论方面实在欠缺，所以还是从最简单的问题练手。

这个系列来自B站Up主“Red-Green鲤鱼”，视频链接

2. 一维非稳态对流扩散方程

\[\frac{\partial f}{\partial t} + U\frac{\partial f}{\partial x} = D \frac{\partial^2 f}{\partial x^2} \]

2.1. 常系数：U和D为定值

方程特解：

\[f(x,t)=\frac{1}{\sqrt{4t+1}}exp \left( -\frac{(x-1-Ut)^2}{D(4t+1)} \right) \]

2.2. 问题描述

用有限差分法求解上述方程，其中\(U=1.0, D=0.05, x\in[0,9]\)，并将数值解与\(t=2.5\)时的解析解对比

2.2.1. 初始条件

\[f(x,0)=exp \left( -\frac{(x-1)^2}{D} \right) \]

2.2.2. 边界条件

直接给出边界的值，为Dirichlet边界条件

\[f(0,t)=\frac{1}{\sqrt{4t+1}}exp \left( -\frac{(1+Ut)^2}{D(4t+1)} \right) \]

\[f(9,t)=\frac{1}{\sqrt{4t+1}}exp \left( -\frac{(8-Ut)^2}{D(4t+1)} \right) \]

3. 方程离散和区域离散 3.1. 区域离散

有限差分法中，将连续的区域离散为一系列结点，每个结点上含有物理量的值。假设结点间等距，距离为\(\delta\)，那么离散方式可以分为内外两种：

1. 结点和边界重合，为外结点法
2. 结点和边界之间相差\(\delta /2\)，为内结点法

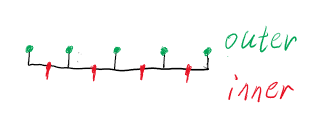
以下将比较两种结点设置的方式。

1. 外结点法：设置\(N+1\)个结点，编号从0~N，结点间距\(\delta = L/N\)，结点\(i\)的坐标为\(x_i=i\cdot \delta\)
2. 内结点法：设置\(N\)个结点，编号从1~N，结点间距\(\delta = L/N\)，结点\(i\)的坐标为\(x_i=i\cdot \delta - \delta /2\)

3.2. 方程离散 3.2.1. 非稳态项

对于结点\(i\)，采用一阶欧拉

\[\frac{\partial f}{\partial t}\bigg|_{i}=\frac{f^{n+1}_i-f^n_i}{\Delta t} \]

3.2.2. 对流项

一阶迎风，由于给出对流项前置系数\(U=1.0\)，因此迎风格式为

\[\frac{\partial f}{\partial x}\bigg|_{i}=\frac{f_i-f_{i-1}}{\delta} \]

3.2.3. 扩散项

二阶中心差分

\[\frac{\partial^2 f}{\partial x^2}\bigg|_{i}=\frac{f_{i+1}-2f_i+f_{i-1}}{\delta ^2} \]

注意：以上离散格式均是针对内结点。

3.3. 差分方程

将以上各项的离散形式组合起来得到差分方程。需要注意的是，如果对流项和扩散项中用到的物理量的值为下一时刻即\(n+1\)时间步的值，则为隐式离散；如果为当前时刻即\(n\)时间步的值，则为显式离散。

为了表示方便，下文中\(i\)用\(P\)表示，\(i-1\)用\(W\)表示，\(i+1\)用\(E\)表示。

3.3.1. 显式

\[f^{n+1}_P=a_P f_P + a_W f_W + a_E f_E \]

\[a_P=1-\frac{U\Delta t}{\delta} -\frac{2D\Delta t}{\delta^2} \]

\[a_W=\frac{U\Delta t}{\delta} + \frac{D\Delta t}{\delta^2} \]

\[a_E=\frac{D\Delta t}{\delta^2} \]

根据Harten定理系数非负原则，该显式格式稳定的条件是\(a_P\)、\(a_W\)、\(a_E\)同时大于0，可见，这三项中只有\(a_P\)存在小于0的可能，通过调整程序中\(\delta\)和\(\Delta t\)能够发现这一现象。

3.3.2. 隐式

\[a_P f^{n+1}_P=a_W f^{n+1}_W + a_E f^{n+1}_E + b \]

\[a_P=1+\frac{U\Delta t}{\delta}+\frac{2D\Delta t}{\delta^2} \]

\[a_W=\frac{U\Delta t}{\delta} + \frac{D\Delta t}{\delta^2} \]

\[a_E=\frac{D\Delta t}{\delta^2} \]

\[b=f^n_P \]

3.4. 边界离散 3.4.1. 外结点法

结点编号从0到N，共N+1个结点，对于结点\(i\in [1,N-1]\)，均采用上述离散方程求解，对于\(i=0,N\)的两个结点，由Dirichlet边界条件直接获得结点上的值。

3.4.2. 内结点法

结点编号从1到N，共N个结点，结点\(i\in [2,N-1]\)按照上述离散方程求解。结点\(i=1,N\)的对流项以及扩散项分别为

3.4.2.1. 对流项

\[\frac{\partial f}{\partial x}\bigg|_{i=1}=\frac{f_1-f_{x=0}}{\delta/2},\quad \frac{\partial f}{\partial x}\bigg|_{i=N}=\frac{f_N-f_{N-1}}{\delta} \]

3.4.2.2. 扩散项：

对于左边界：

\[f_{x=0}=f_0=f_1-\frac{\delta}{2}f^{\prime}+\frac{\delta^2}{8}f^{\prime\prime} + \varepsilon(\delta^3) \\ f_2=f_1+\delta f^{\prime} + \frac{\delta^2}{2} f^{\prime\prime} +\varepsilon(\delta^3) \\ \]

消去\(f^{\prime}\)可得到二阶导数

\[\frac{\partial^2 f}{\partial x^2}\bigg|_{i=1}=\frac{2f_0+f_{2}-3f_1}{\delta ^2 (3/4)}+\varepsilon(\delta) \]

注意：上式只有一阶精度。同理，右边界按类似的方式处理，令右边界为\(N+1\)号结点，则结点\(N\)

\[\frac{\partial^2 f}{\partial x^2}\bigg|_{i=N}=\frac{2f_{N+1}+f_{N-1}-3f_N}{\delta ^2 (3/4)}+\varepsilon(\delta) \]

使用一阶精度扩散项的显式算法：

\[f^{n+1}_1=f_1-\frac{2U\Delta t}{\delta}(f_1-f_0)+\frac{4D\Delta t}{3\delta^2}(2f_0+f_2-3f_1) \]

\[f^{n+1}_N=f_N-\frac{U\Delta t}{\delta}(f_N-f_{N-1})+\frac{4D\Delta t}{3\delta^2}(2f_{N+1}+f_{N-1}-3f_N) \]

使用一阶精度扩散项的隐式算法：

\[\left( 1+\frac{2U\Delta t}{\delta}+\frac{4D\Delta t}{\delta ^2} \right)f_1^{n+1}=\frac{4D\Delta t}{3\delta^2}f_2^{n+1}+ \left( \frac{2U\Delta t}{\delta}+\frac{8D\Delta t}{3\delta^2} \right)f_0^{n+1} + f_1^n \]

\[\left( 1+\frac{U\Delta t}{\delta}+\frac{4D\Delta t}{\delta^2} \right)f_N^{n+1}=\left( \frac{U\Delta t}{\delta}+\frac{4D\Delta t}{3\delta^2} \right)f_{N-1}^{n+1}+\frac{8D\Delta t}{3\delta^2}f_{N+1}^{n+1} + f_N^n \]

上式中的\(f_0^{n+1}\)以及\(f_{N+1}^{n+1}\)均为已知的边界条件。

3.4.2.3. 扩散项二阶精度的补充结点法

这种方法来自《数值传热学》例4-4

对于内结点法，\(i=1\)的结点和左边界距离为\(\delta /2\)，我们在左边界上设置一个结点，编号为\(i=0\)，在左边界往左\(\delta/2\)处补充结点\(i=-1\)，对于结点\(i=1\)

\[\frac{\partial^2 f}{\partial x^2}\bigg|_{i=1}=\frac{f_{2}+f_{-1}-2f_1}{\delta ^2}+\varepsilon(\delta ^2) \]

对于结点\(i=0\)

\[\frac{\partial^2 f}{\partial x^2}\bigg|_{i=0}=\frac{f_{1}+f_{-1}-2f_{0}}{(\delta/2) ^2}+\varepsilon(\delta ^2) \]

由于结点0处于边界，在满足边界条件的同时应尽量让该结点满足控制方程，所以对结点0的控制方程的显式离散为

\[\frac{f_0^{n+1}-f_0^n}{\Delta t}+U\frac{f_0-f_{-1}}{\delta /2}=D\frac{f_{1}+f_{-1}-2f_{0}}{(\delta/2) ^2} \]

\(f_0^{n+1}\)以及\(f_0^n\)为Dirichlet边界条件，均已知，因此可求出\(f_{-1}\)，将\(f_{-1}\)代入结点\(i=1\)的扩散项差分方程中，最终可得到满足空间二阶精度的扩散项差分方程。

4. 代数方程组求解方法

显式离散能够直接推导出物理量的更新方程，因此只要给出\(\Delta x\)和\(\Delta t\)便能求解，但因为稳定性条件（如Harten定理）限制了所能采用的\(\Delta t\)

隐式离散的稳定性更好，但是需要联立求解方程组。空间被离散为\(N\)个结点，每个结点都对应一个方程，即\(N\)个方程\(N\)个未知数。方程组求解的快慢直接决定了整个计算流程的效率，因此研究者开发了若干方程组求解方法，可分为两大类，直接求解和迭代求解

4.1. 直接求解

当求解的未知数个数极少时，采用Cramer法则直接求解。本文讨论的一维问题中，每个结点只和周围两个结点相关，即\(a_P\)只和\(a_W\)以及\(a_E\)相关，因此，求解的代数方程组只有三个对角上的元素非零，即三对角矩阵。下面介绍针对该矩阵发展的算法，基于Gauss消元法的Thomas算法：TDMA

4.1.1. TDMA: Tridiagonal matrix method

为了节省篇幅，以下只讨论区域离散方式为外结点法的代数方程组求解。事实上有限体积法的离散方式更像内结点法，因为体心值作为网格平均值有二阶精度（参考链接）。

矩阵形式为\(AX=B\)，由于使用了第一类边界条件，\(x_1\)和\(x_N\)已知，因此\(a_{12}=a_{N,N-1}=0\)

\[\left[ \begin{matrix} a_{11} & a_{12} & & & & \\ a_{21} & a_{22} & a_{23} & & & & \\ & & & \cdots \\ & & a_{i,i-1} & a_{ii} & a_{i,i+1} & & \\ & & & \cdots \\ & & & & a_{N-1,N-2} & a_{N-1,N-1} & a_{N-1,N} \\ & & & & & a_{N,N-1} & a_{N,N} \\ \end{matrix} \right] \left[ \begin{matrix} x_{1} \\ x_{2} \\ \cdots \\ x_{i} \\ \cdots \\ x_{N-1} \\ x_{N} \end{matrix} \right]= \left[ \begin{matrix} b_{1} \\ b_{2} \\ \cdots \\ b_{i} \\ \cdots \\ b_{N-1} \\ b_{N} \end{matrix} \right] \]

TDMA算法包含两个步骤，消元和回代。消元指的是通过将上一行整体加到下一行从而消去下一行最左边的元素，从矩阵形状上来看就是将三对角矩阵变成了上对角矩阵，此做法的目的是将最后一行的\(a_{N,N-1}\)消去从而能直接计算出\(x_N\)，得到\(x_N\)后便逐一向上回代解出其他未知数。

为了讨论方便，把通式写成\(A_iT_i=B_iT_{i+1}+C_iT_{i-1}+D_i\)，消元的目的是把该式化为\(T_{i-1}=P_{i-1}T_i+Q_{i-1}\)，通过整理可以得到系数\(P_i,Q_i\)和\(B_i,C_i,D_i\)之间的关系，

\[P_i=\frac{B_i}{A_i-C_iP_{i-1}},\quad Q_i=\frac{D_i+C_iQ_{i-1}}{A_i-C_iP_{i-1}} \]

可以看出，\(P_i\)和\(Q_i\)都需要递归求解

\[P_1=\frac{B_1}{A_1},\quad Q_1=\frac{D_1}{A_1},\quad Q_N=T_N \]

综上，TDMA计算流程为

1. 计算\(P_1,Q_1\)
2. 更新\(P_i,Q_i\)，得到\(P_N,Q_N\)，其中\(Q_N=T_N\)
3. 由\(T_{i-1}\)的表达式计算\(T_1-T_{N-1}\)

4.2. 迭代求解

待补充

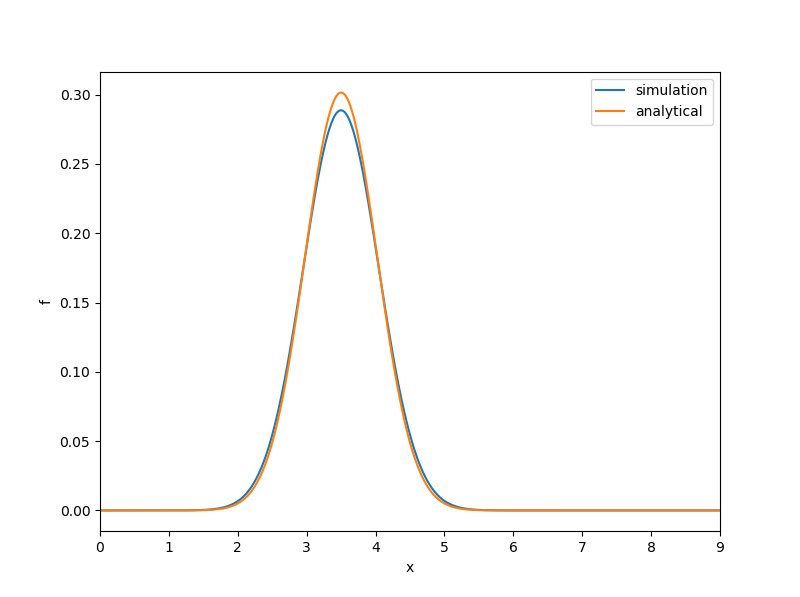
5. 计算结果讨论 5.1. 显式格式

由上述离散过程可见，对流项采用一阶迎风。一阶格式的结果是截断项首项为二阶导数，而二阶导数项有扩散性质，即物理量会向各个方向传播。通常这种由二阶导数引起的扩散现象称为假扩散/人工粘性/数值粘性。具体讨论可参考《数值传热学》第二版5.5节。

下图为显式离散在\(t=2.5s\)的计算结果，区域离散方式为外结点和内结点的差别不大。结点间距\(\Delta x=0.009\)，时间步\(\Delta t=0.0001s\)，该步长满足Harten定理。可见，模拟结果与解析解相比，有矮胖特征，意味着存在假扩散现象。

5.2 隐式格式

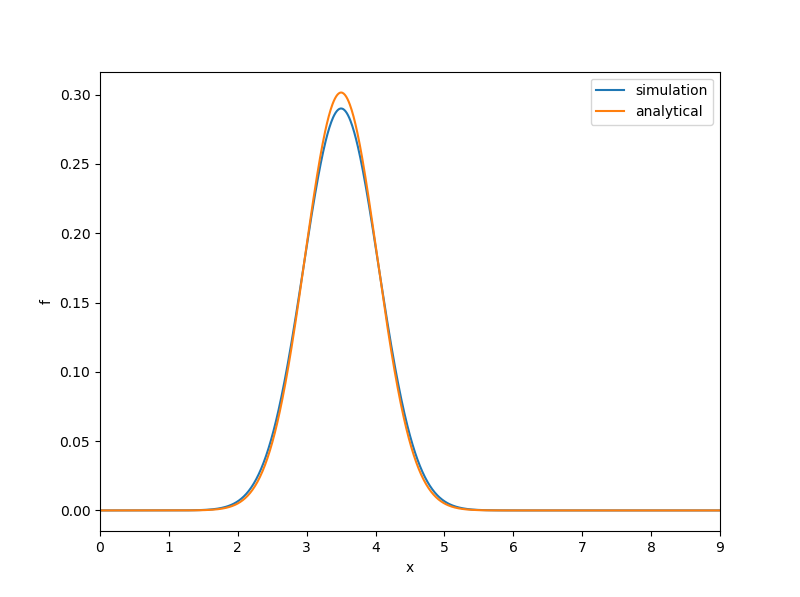
下图为隐式离散在\(t=2.5s\)的计算结果，区域离散采用外结点，结点间距0.009，时间步\(\Delta t=0.001s\)，而在相同时间步下，显式格式的计算结果会发散，比较来看，隐式格式能够适用更大的时间步长。