基础数论学习笔记

数论：费马小定理，乘法逆元，威尔逊定理，扩展欧几里得算法，欧拉函数，离散对数问题（大步小步算法 BSGS），线性同余方程组（中国剩余定理 CRT），数论分块，阶与原根，高次剩余问题，卢卡斯定理。 CHANGE LOG

• 2021.12.6. 重构文章，删去线性筛部分，修改部分表述。
• 2022.3.15 二次重构文章。
• 2022.3.23 三次重构文章。
• 2022.3.24 重构完成，新增威尔逊定理，素数在阶乘和组合数中的幂次，阶与原根，高次剩余和卢卡斯定理。

0. 前置知识 0.1 基本定义与记号

Abstractness is the price of generality.

读者需要知道一些数论相关的基本概念，如同余符号 \(\equiv\) 及其含义，最大公约数 \(\gcd\)，并掌握基本数论算法如快速幂，辗转相除法求解 \(\gcd\)。

• 整除：若非零整数 \(a\) 是整数 \(b\) 的因数即 \(b \bmod a = 0\)，则称 \(a\) 整除 \(b\) 或 \(b\) 被 \(a\) 整除，记作 \(a\mid b\)。若反之则称 \(a\) 不能整除 \(b\) 或 \(b\) 不能被 \(a\) 整除，记作 \(a\nmid b\)。
• 同余：\(a\equiv b\pmod p\) 表示整数 \(a\) 和 \(b\) 模正整数 \(p\) 的余数相等。
• 最大公约数：整数 \(a\) 和 \(b\) 的最大公约数是最大的整数 \(d\) 使得 \(d\) 整除 \(a\) 且 \(d\) 整除 \(b\)，记作 \(\gcd(a, b)\)。\(\gcd(a, b)\) 在不引起歧义的前提下有时会简写为 \((a, b)\)。
• 互质：若整数 \(a, b\) 满足 \(\gcd(a, b) = 1\)，则称 \(a, b\) 互质，记作 \(a\perp b\)。一般 \(a, b\) 均为非负整数。注意，\(\gcd(0, i) = i(i \geq 0)\)，\(1\) 和任何整数互质。
• \(\mathbb P\) 表示素数集。
• 剩余类：模 \(n\) 同余的所有数构成的等价类被称为模 \(n\) 的剩余类。它们等价，因为我们在模 \(n\) 意义下讨论它们。模 \(n\) 余 \(i\) 的剩余类记作 \(K_i\)。容易发现模 \(n\) 的剩余类共 \(n\) 个。
• 完全剩余系：从 \(n\) 个模 \(n\) 剩余类中各选一个数 \(a_0, a_1, \cdots, a_{n - 1}\)，它们构成模 \(n\) 的完全剩余系。
• 简化剩余系：从与 \(n\) 互质的剩余类中各选一个数 \(a_1, a_2, \cdots, a_k\)，它们构成模 \(n\) 的简化剩余系。读者在接下来的章节中将了解到，\(k\) 等于 \(\varphi(n)\)。简化剩余系又称为 既约剩余系 或 缩系。
• 乘法逆元：若 \(ax \equiv 1 \pmod p\)，则称 \(x\) 为 \(a\) 在模 \(p\) 意义下的乘法逆元，记作 \(a ^ {-1}\)。
• 质因子次数：\(n\) 当中质因子 \(p\) 的次数记作 \(v_p(n)\)。即 \(p ^ {v_p(n)} \mid n\) 且 \(p ^ {v_p(n) + 1} \nmid n\)。严格意义上应记为 \(\nu_p(n)\)（希腊字母 nu）。为方便，本文暂记为 \(v_p(n)\)。
• 各位数字之和：\(n\) 在 \(p\) 进制下的各位数字之和记作 \(s_p(n)\)。

0.2 费马小定理

当 \(p\) 是质数时，其因子只有 \(1\) 和 \(p\) 两个。因此，若两个数相乘是 \(p\) 的倍数，其中必然至少有一个是 \(p\) 的倍数。

当 \(a\) 不是 \(p\) 的倍数时，不存在 \(x \neq y\) 且 \(1 \leq x, y < p\) 使得 \(xa \equiv ya\pmod p\)，因为这需要 \(x - y\) 是 \(p\) 的倍数，与 \(1\leq x, y< p\) 的限制矛盾。

考虑 \(1\sim p - 1\) 的所有数，它们乘以 \(a\) 之后在模 \(p\) 意义下互不相同，说明仍然得到 \(1\sim p - 1\) 的所有数。

因此，\(\prod\limits_{i = 1} ^ {p - 1} i \equiv \prod\limits_{i = 1} ^ {p - 1} ai \pmod p\)，即

\[a ^ {p - 1} \equiv 1 \pmod p \]

上述结论称为 费马小定理。根据推导过程，它适用于 \(p\) 是质数且 \(a\) 不是 \(p\) 的倍数的情形。

0.3 模意义下乘法逆元

根据费马小定理，当 \(p\) 为质数时，

\[a ^ {-1} \equiv a ^ {p - 2} \pmod p \]

据此可快速幂求出一个数在模质数意义下的乘法逆元。

当 \(p\) 非质数时，\(a\) 有乘法逆元的充要条件为 \(a \perp p\)。我们将在第一章展开讨论。

给出一些模 质数 \(p\) 意义下求乘法逆元的常见技巧。

1. 线性求逆元：考虑 增量法。假设 \(1\sim i-1\) 的逆元已知。设 \(p = ki + r(0\leq r < i)\)，即 \(k\) 和 \(r\) 分别是 \(p\) 对 \(i\) 做带余除法的商和余数。因为 \(ki + r \equiv 0 \pmod p\)，两边同时除以 \(ir\)，得 \(i ^ {-1} \equiv -kr ^ {-1}\equiv -\left\lfloor \dfrac p i \right\rfloor (p\bmod i) ^ {-1}\)。时间复杂度线性。

2. 线性求任意 \(n\) 个数 \(a_i(1 \leq a_i < p)\) 的逆元：设 \(s\) 为 \(a\) 的前缀积。算出 \(s_n ^ {-1}\) 后通过 \(s_i ^ {-1} = s_{i + 1} ^ {-1} \times a_{i + 1}\) 得到前缀积的逆元，则 \(a_i^{-1}=s_{i-1}\times s_i^{-1}\)。时间复杂度 \(\mathcal{O}(n+\log p)\)。

0.4 威尔逊定理

由于乘法逆元成对出现，这启发我们思考，\(1\sim p - 1\) 所有数能否两两配对互为逆元？若可以，那么说明当 \(p\) 是质数时，\((p - 1)! \equiv 1\pmod p\)。

可以，但不完全可以，因为 \(1\) 和 \(-1\) 的逆元均为它本身，且仅有这两个数满足 \(x ^ 2\equiv 1\pmod p\)。这符合我们的直观认知，毕竟在实数域下 \(x ^ 2 = 1\) 有且仅有解 \(\pm 1\)。

证明：求解方程 \(x ^ 2\equiv 1\pmod p\)。移项，使用平方差公式，\((x - 1)(x + 1) \equiv 0\pmod p\)。显然，为使等式左端等于 \(0\)，必然有 \(x \equiv \pm 1\pmod p\)。证毕。

因此，我们需要对结论进行一些修正，即当 \(p\) 是质数时，\((p - 1) ! \equiv 1 \times (p - 1) \equiv -1\pmod p\)。特殊考虑 \(p = 2\)，发现符合该结论。

既然有了充分条件，我们自然会考虑 \(p\) 不是质数的情况。

1. 当 \(p\) 为完全平方数 \(q ^ 2\) 时，考虑 \(q\) 和 \(2q\)。它们相乘后模 \(p\) 等于 \(0\)。因此，若 \(2q < p\) 即 \(p\) 为大于 \(4\) 的完全平方数时，\((p - 1)!\equiv 0\)。

2. 当 \(p = 4\) 时，\(3 ! \equiv 2\pmod 4\)。

3. 当 \(p\) 为大于 \(4\) 的非完全平方数时，令 \(q\) 为 \(p\) 的最小质因子，则 \(q \neq \dfrac p q\)，故 \((p - 1)!\equiv 0\pmod p\)。

综上，我们得到了 威尔逊定理：\((p - 1)!\equiv 1\pmod p\) 与 \(p\) 是质数等价。

---

我们尝试将威尔逊定理扩展至素数的幂的情形，即考虑 \(p ^ k\) 以内所有与 \(p\) 互质的数的乘积模 \(p ^ k\)，记为 \((p ^ k!)_p\)。

仍然考虑求解 \(x ^ 2 \equiv 1\pmod {p ^ k}\) 即求出逆元为本身的数，并将非 \(x\) 的其它所有数与其逆元两两配对（因为我们只考虑与 \(p\) 互质的数，所以其在模 \(p ^ k\) 意义下显然存在逆元），这说明我们只需考虑所有 \(x\) 的乘积。

因式分解得到 \((x + 1)(x - 1)\equiv 0\pmod {p ^ k}\)。

注意到当 \(p > 2\) 时，\(x + 1\) 和 \(x - 1\) 不可能均是 \(p\) 的倍数，因此必然有 \(x + 1\equiv 0\pmod {p ^ k}\) 或 \(x - 1\equiv 0\pmod {p ^ k}\)。这和一般情况等价，因此仍然有 \((p ^ k!)_p\equiv -1\pmod {p ^ k}\)。

当 \(p = 2\) 时，\(x + 1\) 和 \(x - 1\) 可能同时为 \(2\) 的倍数，但不可能同时为 \(4\) 的倍数。因此，若 \(x + 1\) 和 \(x - 1\) 同时为 \(2\) 的倍数，除掉不能被 \(4\) 整除的那个数的质因子，得到 \(x + 1\equiv 0\pmod {2 ^ {k - 1}}\) 或 \(x - 1\equiv 0\pmod {2 ^ {k - 1}}\)。这说明当 \(p = 2\) 时方程有四个解 \(\pm 1\) 和 \(2 ^ {k - 1}\pm 1\)。注意，当 \(k = 1\) 时四个根均重合，此时 \(1!\equiv 1\equiv -1\pmod 2\)；当 \(k = 2\) 时两对根重合，此时 \(1\times 3\equiv -1\pmod 4\)。否则 \(1\times (-1) \times (2 ^ {k - 1} + 1) \times (2 ^ {k - 1} - 1)\equiv 1\pmod {2 ^ k}\)。

综合上述两种情况，我们得到如下推论

\[(p ^ k!)_p \equiv \begin{cases} 1 & p = 2 \land k \geq 3 \\ -1 & {\rm otherwise}\end{cases} \]

在 exLucas 中用到了该结论。

0.5 素数在阶乘中的幂次

给定正整数 \(n\) 和质数 \(p\)，求 \(v_p(n!)\)。

我们考虑将 \(1\sim n\) 当中所有 \(p\) 的倍数提出来，然后全部除以 \(p\)。这一步消掉的质因子个数为 \(\left\lfloor \dfrac n p \right\rfloor\)，因为 \(1\sim n\) 当中 \(p\) 的倍数有 \(\left\lfloor \dfrac n p \right\rfloor\) 个。

上一步操作后，我们得到了 \(1 \sim \left\lfloor \dfrac n p \right\rfloor\)。我们将其中所有 \(p\) 的倍数提出来，然后全部除以 \(p\)。这一步消掉的质因子个数为 \(\left\lfloor \dfrac n {p ^ 2} \right\rfloor\)。

以此类推，直到 \(\left\lfloor \dfrac n {p ^ k} \right\rfloor < p\)。此时已经没有 \(p\) 的倍数了。

因此，我们有如下结论：

\[v_p(n!) = \sum_{i = 1} ^ {\lfloor\log_p n\rfloor} \left\lfloor \dfrac n {p ^ i} \right\rfloor \]

• 这一定理由勒让德（Legendre）在 1808 年提出。

考虑换一种方法求和。我们尝试对 \(n\) 在 \(p\) 进制下的每一位，求出它对每次提出因子个数的贡献之和。不妨设 \(n = \sum\limits_{i = 0} ^ c a_i p ^ i\)，则

\[\begin{aligned} v_p(n!) & = \sum_{i = 1} ^ {c} \sum_{j = 0} ^ c\left\lfloor \dfrac {a_j p ^ j} {p ^ i} \right\rfloor \\ & = \sum_{j = 0} ^ c \sum_{i = 1} ^ {j} \dfrac {a_j p ^ j} {p ^ i} \\ & = \sum_{j = 0} ^ c a_j\sum_{i = 0} ^ {j - 1} p ^ i \\ & = \sum_{j = 0} ^ c a_j\dfrac {p ^ j - 1} {p - 1} \\ & = \dfrac {\left(\sum_{j = 0} ^ c a_j p ^ j\right) - \left(\sum_{j = 0} ^ c a_j\right)}{p - 1} \\ & = \dfrac {n - s_p(n)}{p - 1} \end{aligned} \]

通过上述推导，我们得到了 \(v_p(n!)\) 的另一种表示方法 \(\dfrac {n - s_p(n)}{p - 1}\)。

特别地，当 \(p = 2\) 时，\(v_2(n) = n - \mathrm{popcount}(n)\)。

0.6 素数在组合数中的幂次

根据 0.5 节的结论以及组合数公式 \(\dbinom n m = \dfrac {n!} {m!(n - m)!}\)，我们有

\[\begin{aligned} & v_p\left(\dbinom n m\right) \\ = \ &\dfrac {n - s_p(n) - (m - s_p(m)) - (n - m - s_p(n - m))}{p - 1} \\ = \ &\dfrac {s_p(m) + s_p(n - m) - s_p(n)}{p - 1} \end{aligned} \]

考虑 \(n - m\) 和 \(m\) 在 \(p\) 进制 下相加得到 \(n\) 的过程，其中 \(p\) 是质数。每产生一次进位，各位数字之和就会减少 \(p - 1\)，因此 \(p\) 在组合数 \(\dbinom n m\) 中的幂次 \(v_p\left(\dbinom n m\right)\) 即 \(p\) 进制下 \(n - m\) 加上 \(m\) 需要进位的次数，也等于 \(n\) 减去 \(m\) 需要借位的次数。

上述结论被称为 Kummer 定理，在 Lucas 定理中有用。

0.7 其它有用的事实

因为这个结论非常经典且容易理解，但证明较繁琐，故写在此处。

在一个长为 \(n\) 的环上每一步走 \(k\) 条边，形成的子环个数为 \(\gcd(n, k)\) 且环长为 \(\dfrac n {\gcd(n, k)}\)。

感性理解：给环编号，走到的点的编号模 \(\gcd(n, k)\) 一定相同，且可以证明一定能走到所有编号模 \(\gcd(n, k)\) 相同的点。

证明：令 \(d = \gcd(n, k)\)，按顺序为环上的每个点标号 \(0, 1, 2, \cdots, n - 1\)，即 \(0\to 1 \to \cdots\to n - 1 \to 0\)。从 \(r\) 开始每一步走 \(k\) 条边，到达的点必然与 \(r\) 在模 \(d\) 意义下同余，因为 \(n,k\) 均为 \(d\) 的倍数，为 \(r\) 加上 \(k\) 之后对 \(n\) 取余并不影响 \(r\bmod d\)。

首先证明一个引理：当 \(n \perp k\) 时，从环上任意一个节点出发，能够走遍所有点。

证明：不妨设从点 \(r\) 开始，则走 \(x\) 步后到达的节点编号即 \((r + kx)\bmod n\)。欲证原结论，只需证明对于任意 \(0\leq i < j < n\)，均有 \(r + ik \not \equiv r + jk\pmod n\)，即走 \(0\sim n - 1\) 步到达的节点互不相同。

考虑反证法，假设存在 \(r +ik\equiv r +jk\pmod n\)，移项得到 \((j - i)k \equiv 0\pmod n\)。因为 \(k\perp n\)，所以 \(n \mid j - i\)，这与 \(0\leq i, j < n\) 矛盾。得证。

通过上述推导过程我们也可以看出，反证法在证明两个数不相等时非常有用。

不妨设 \(0\leq r < d\)。考虑 \(0\sim n - 1\) 当中所有模 \(d\) 余 \(r\) 的数 \(r, r + d, \cdots, r + \left(\dfrac n d - 1\right)d\)，将其重标号为 \(0, 1, \cdots, \dfrac n d - 1\)，形成一个长为 \(\dfrac n d\) 的子环。因为 \(d = \gcd(n, k)\)，所以 \(\dfrac n d\perp \dfrac k d\)。根据引理，在这个长为 \(\dfrac n d\) 的子环上每一步走 \(\dfrac k d\) 条边（相当于在原环上走 \(k\) 条边），能够走遍子环上每一个点。

因此形成的子环长为 \(\dfrac n d\) 即 \(\dfrac n {\gcd(n, k)}\)，且每一个模 \(d\) 的剩余系均恰好形成一个子环，因此子环个数为 \(d\)，即 \(\gcd(n, k)\)。或者说，子环长乘以子环个数等于环长，因为每个模 \(d\) 的剩余系即每一个子环是等价的，均为在 \(0\sim n - 1\) 内模 \(d\) 相同的所有数，只是子环之间在原环上的标号模 \(d\) 不同。证毕

相关应用见 P5582 [SWTR-01] Escape，P5887 Ringed Genesis，P6187 [NOI Online #1 提高组] 最小环。

1. 扩展欧几里得算法

扩展欧几里得算法简称扩欧或 exgcd。它是求解最大公约数的欧几里得算法的扩展，用于求解形如 \(ax + by = c\) 的 二元 线性不定方程。

我们将看到扩展欧几里得算法与最大公约数的联系。

1.1 解的存在性

在求解形如 \(ax + by = c\) 的不定方程之前，我们首先需要知道如何 判定 它有解。

• 在求解方程之前，首先需要判断解的存在性。

先考虑一些较弱的结论。容易发现，无论 \(x, y\) 的取值，左式一定是 \(d = \gcd(a, b)\) 的倍数。因此，当 \(d\nmid c\) 时，方程显然无解。这使得我们可以为方程两侧同时除以 \(d\)。

同时，我们注意到为 \(a\) 和 \(b\) 同时除以 \(d\) 之后，\(a, b\) 互质。这说明我们将问题简化为求解 \(a, b\) 互质时的情形。可见优先判断解的存在性的重要性。

根据直观感受，对于 \(a\perp b\)，\(ax + by\) 似乎能组合成任意一个整数，因为它们没有共同质因子。显然，这只需证明 \(ax\bmod b\) 可以取到 \(0 \sim b - 1\) 当中的任何一个数。

证明是容易的，因为 \(a\perp b\) 提供了很强的性质。注意到这实际上是将费马小定理的证明中，\(p\) 为质数的条件去掉了，换成了 \(a \perp p\)，本质并没有差别。

考虑 \(ax\) 和 \(ay\) 满足 \(1\leq x, y \leq b\) 且 \(x\neq y\)，则 \(ax\not\equiv ay \pmod b\)。若存在，则 \(a(x - y)\equiv 0\pmod b\)。因为 \(a\perp b\)，所以 \(x - y \equiv 0\pmod b\)（\(a\) 能够约去的原因是它不提供任何 \(b\) 含有的质因子，也就是对使得 \(a(x - y)\equiv 0\pmod b\) 成立没有任何 “贡献”），这与 \(1\leq x, y \leq b\) 的限制矛盾。证毕。

因为 \(ax + by\) 在 \(a\perp b\) 时取遍所有整数，所以若 \(d\mid c\)，方程就一定有解。

综合上述结论，我们得到了判断二元线性不定方程 \(ax + by = c\) 存在解的 充要条件：\(\gcd(a, b) \mid c\)。这被称为 裴蜀定理 或 贝祖定理。

1.2 算法介绍

欲求解 \(ax + by = c\)，设 \(d = \gcd(a, b)\)，我们只需求解 \(ax + by = d\)，并将解乘以 \(\dfrac c d\)。根据裴蜀定理，方程的解必然存在。

注意到等式右端等于 \(x, y\) 前系数的最大公约数。回顾欧几里得算法（即辗转相除法），我们用到了关键结论 \(\gcd(a, b) = \gcd(b, a\bmod b)\)，将问题缩至更小的规模上。利用这一思想，我们尝试将求解的方程也缩至更小的规模上。

考虑 递归构造。假设我们已经得到了 \(bx' + (a \bmod b) y' = d\) 的一组解，则

\[\begin{aligned} ax + by & = bx' + (a\bmod b) y' \\ & = bx' + \left(a - b \times \left\lfloor \dfrac a b \right\rfloor \right)y' \\ & = ay' + b \left(x' - \left\lfloor \dfrac a b \right\rfloor y' \right) \end{aligned} \]

对比等式两端，有 \(x = y'\)，\(y = x' - \left\lfloor \dfrac a b \right\rfloor y'\)，递归计算即可。递归边界即当 \(b = 0\) 时，根据辗转相除法，\(a = d\)，故此时 \(x = 1\)，\(y = 0\) 即为一组解。

上述过程即扩展欧几里得算法，时间复杂度是辗转相除法的 \(\log V\)。代码如下。

void exgcd(int a, int b, int &x, int &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}

注意，扩欧求得的解为 \(ax + by = d\) 的一组特解。为求得原方程 \(ax + by = c\) 的一组特解，还需将 \(x, y\) 乘以 \(\dfrac c d\)。

1.3 解的形式与数值范围

显然，不定方程 \(ax + by = c\) 若存在解，则存在无穷解。我们需要通解的表示形式。

扩欧可以求得一组特解 \(x_0, y_0\)。根据 \(\Delta(ax)+\Delta(by)=0\)，设 \(\Delta=|{\Delta(ax)}|=|\Delta(by)|\)，那么 \(a,b\mid \Delta\)，故 \(\mathrm{lcm}(a,b)\mid \Delta\)。因此 \(|\Delta x|\) 是 \(\dfrac{\mathrm{lcm}(a, b)} a = \dfrac b d\) 的倍数，\(|\Delta y|\) 同理。故通解形如

\[\begin{cases} x = x_0 + \dfrac b d k \\ y = y_0 - \dfrac a d k \end{cases} \quad (k \in \Z) \]

特解的数值范围详见 ycx 的博客 关于 exgcd 求得特解的数值范围。这里仅给出结论：对于非平凡情况，有 \(|x| \leq \left| \dfrac b {2d} \right|\) 且 \(|y| \leq \left |\dfrac a {2d}\right|\)。平凡情况：\(a = b = 1\) 或 \(b = 0\)。

1.4 应用

1. exgcd 的重要应用是求解一元线性同余方程 \(ax\equiv b \pmod p\)。只需将其看成二元不定方程 \(ax + py = b\) 并使用 exgcd 求解即可。

2. 当模数不是质数时，费马小定理不再适用，但模意义下的乘法逆元仍可能存在。\(a\) 在模 \(p\) 意义下存在逆元当且仅当 \(a \perp p\)，因为求逆元相当于求解 \(ax \equiv 1 \pmod p\) 即使得 \(ax + py \equiv 1\pmod p\) 成立的 \(x\)。根据裴蜀定理，\(x\) 存在当且仅当 \(a\perp p\)。求解模 \(p\) 意义下 \(a\) 逆元只需求解线性同余方程 \(ax\equiv 1\pmod p\) 即可。

int inv(int a, int p) {return exgcd(a % p, p, a, *new int), (a % p + p) % p;}

3. 通过 exgcd 我们可以证明 \(ax\equiv b\pmod p\) 在当 \(\gcd(a, p)\nmid b\) 时无解，否则在 \(0\sim p - 1\) 中有 \(\gcd(a, p)\) 个整数解。这是因为其通解可写为 \(x_0 + \dfrac p {\gcd(a, p)}\) 的形式，其中 \(0\leq x_0 < \dfrac {p}{\gcd(a, p)}\)：将方程两侧同时除以 \(\gcd(a, p)\)，则 \(\dfrac {a}{\gcd(a, p)} x_0 \equiv \dfrac {b}{\gcd(a, p)} \pmod {\dfrac p{\gcd(a, p)}}\)。
4. 从裴蜀定理的推导过程中，我们证明了这样一个引理：若 \(a\perp b\)，则 \(ax \bmod b\) 取遍 \(0\sim b - 1\)。这是一个很有用的事实。

1.5 例题 I. UVA10104 Euclid Problem

exgcd 的模板题。

II. P5656【模板】二元一次不定方程 (exgcd)

题目要求 \(x\) 是正整数，可以先求出 \(x\) 的最小正整数值 \(x_0 = x \bmod {\dfrac b d}\)，此时 \(y_{\max} = \dfrac {c - ax_0} b\)。若 \(y_{\max} > 0\) 则有正整数解，且 \(y_{\max}\) 对应正整数解中最大的 \(y\)，否则没有正整数解。对于 \(y_0\) 和 \(x_{\max}\) 同理。

#include <bits/stdc++.h>
using namespace std;

#define int long long
int T, a, b, c;
void exgcd(int a, int b, int &x, int &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
signed main() {
	cin >> T;
	while(T--) {
		scanf("%lld %lld %lld", &a, &b, &c);
		int d = __gcd(a, b), x, y, xx, xy, yx, yy;
		if(c % d) {puts("-1"); continue;}
		exgcd(a, b, x, y);
		x *= c / d, y *= c / d;
		xx = x % (b / d);
		if(xx <= 0) xx += b / d;
		xy = (c - a * xx) / b;
		yy = y % (a / d);
		if(yy <= 0) yy += a / d;
		yx = (c - b * yy) / a;
		if(xy <= 0) cout << xx << " " << yy << "\n";
		else cout << (yx - xx) / (b / d) + 1 << " " << xx << " " << yy << " " << yx << " " << xy << "\n";
	}
	return 0;
}

*III. UVA12775 Gift Dilemma

题意简述：给出 \(a, b, c, p\)，求 \(ax + by + cz = p\) 非负整数解的个数。

题目条件 \(c\geq 200\times \gcd(a, b, c)\) 即 \(c\geq 200\)。对于这种三元不定方程，考虑枚举 \(c\) 前的系数 \(z\)，再求 \(ax + by = p - cz\) 的非负整数解的个数。

记 \(z=\dfrac{p}{c}\)，则时间复杂度为 \(\mathcal{O}(Tz\log z)\)。

IV. 某模拟赛 你还没有 AK 吗

\(x, y\) 分别从 \([0, n]\) 和 \([0, m]\) 中随机选择，求执行任意正整数次 \(x\gets x + y\) 以及 \(y\gets x + y\) 后使得 \(x = X\) 的初始值 \(x, y\) 的个数。\(T\le 10^5\)，\(n, m, X\leq 10 ^ {18}\)。时限 1s。

转化题意，令 \(f_1 = f_2 = 1\)，\(f_i = f_{i - 1} + f_{i - 2}\) 则相当于求有多少对 \((x, y)\) 满足 \(f_{2k + 1}x + f_{2k + 2}y = X\)。

注意到斐波那契数列的增长相当快，当 \(k >\mathcal{O}(\log X)\) 光是 \(f_{2k+1}\) 就已经 \(>X\) 显然不符题意，故考虑直接枚举 \(k\)。

问题转化为求关于 \(x, y\) 的二元一次方程 \(ax + by = X\) 有多少解满足 \(x\in[0, n]\)，\(y\in[0, m]\)（斐波那契数列相邻两项 \(\gcd = 1\)，故不需求 \(\gcd\)）容易 exgcd 求解。但 \(T\log ^ 2 X\) 无法通过。

不难发现只有本质不同的 \(k\) 对 \(a, b\)，故预先存储下来即可将复杂度优化至 \(\mathcal{O}(T\log X)\)。更进一步地，我们有 \(f_{2k + 1} ^ 2\equiv 1 \pmod {f_{2k + 2}}\)（可以归纳证明 \(f_{2k} ^ 2\equiv -1\pmod {f_{2k + 1}}\) 以及上述结论），故直接令 \(x \gets f_{2k + 1}\) 即一个合法解，甚至不需要使用 exgcd。

*V. P3421 [POI2005]SKO-Knights

巧妙线性代数题。题目要求我们找到两个向量 \(d, e\)，使得它们的 整系数 线性组合得到的线性空间（简称整系数线性空间）等价于给出的所有向量的整系数线性空间。定义 \(\mathrm{span}(S)\) 表示向量集合 \(S\) 的整系数线性空间，即

\[\mathrm{span}(S) = \left\{\sum\limits_{a_i\in S} c_ia_i\ (c_i\in \mathbb{Z})\right\} \]

如果我们能将三个向量 \(a, b, c\) 合并成与之等价的两个向量 \(d, e\)，就能够解决本题。根据基础的线性代数知识，不改变矩阵行空间的初等行变换有三种：

• 兑换：对应本题即可以任意交换 \(a, b, c\)。
• 倍乘变换：对应本题即向量可以乘以任意非 \(0\) 整数。
• 倍加变换：对应本题即向量可以加上任意整数倍其它向量。

当然，上述性质仅在 实系数 线性组合的前提下成立。当要求系数为 整数 时，

• 兑换显然不改变矩阵行空间。
• 倍乘变换 可能改变 矩阵行空间，因为 整数乘法不可逆。如 \(\mathrm{span}((0, 1), (1, 0))\neq \mathrm{span}((0, 2), (1, 0))\)，前者是任意整点，后者是任意纵坐标是偶数的整点。
• 倍加变换 不改变 矩阵行空间：对于任意 \(p = y(a + xb) + zb\in \mathrm{span}(a + xb, b)\)，它本质上仍是 \(a, b\) 的整系数线性组合 \(ya + (xy + z)b\)。对于任意 \(p = ya + zb \in \mathrm{span}(a, b)\)，我们也总可以将其表示为 \(a + xb\) 和 \(b\) 的整系数线性组合 \(y(a + xb) + (z - xy) b\)。

很好！如果整系数倍加变换不改变整系数意义下的矩阵行空间，就可以使用 辗转相减法。具体地，考虑两个向量 \(a, b\)，我们能够在 不改变其整系数线性空间 的前提下，将 \(b\) 的某一维变为 \(0\)。只需对 \(a, b\) 在这一维进行辗转相减法即可。

考虑三个向量 \(a, b, c\)，我们对 \(a, b\) 在 \(x\) 这一维进行辗转相减，再对 \(a, c\) 在 \(x\) 这一维进行辗转相减。此时 \(x_b, x_c\) 均为 \(0\)，意味着 \(b, c\) 共线。因此，对 \(b, c\) 在 \(y\) 这一维进行辗转相减，就可以使 \(y_b\gets \mathrm{gcd}(y_b, y_c)\)，而 \(c\) 变成了 零向量，对 \(\mathrm{span}(a, b, c)\) 没有任何贡献，可以 直接舍去，即此时 \(\mathrm{span}(a, b, c) = \mathrm{span}(a, b)\)。

综上，我们在 \(\mathcal{O}(n\log V)\) 的时间内解决了问题，其中 \(V\) 是值域。

注意点：题目限制了坐标绝对值不超过 \(10 ^ 4\)，因此辗转相减法得到最终的 \(a\) 时，\(x_a\) 和 \(y_b\) 是原坐标的 \(\gcd\)，显然满足坐标限制。但 \(y_a\) 不一定，因此要对 \(y_b\) 取模，也相当于做了一步辗转相减（此时 \(x_b = 0\) 所以不需要改变 \(x_a\)）。故最终得到的坐标绝对值不超过 \(10 ^ 2\)，比题目限制优一个数量级。

从上述过程中，我们也可以发现一个有趣的性质：整系数 意义下，两个向量可以在不改变其张成的前提下，使其中一个向量的 某一维变成 \(0\)，而另一个向量的对应维变成原来两个向量在这一维上的 \(\gcd\)。这也是解决本题的关键性质。

因此，推广到任意维度 \(k\)，给定 \(n\) 个 \(k\) 维向量，我们可以 \(nk ^ 2\log V\) 求出这组向量在整系数意义下的基。诶，等等？这不就是 线性基 么！

---

让我们更加深入地钻研一下题解区的做法。

实际上两者的核心思想是等价的，均为刚才提到的性质：将两个向量的其中一个的某一维变成 \(0\)，另一个的对应维变成 \(\gcd\)。不同点在于本文的线性代数做法是从 倍加变换 和 辗转相除法 开始，推得 这一核心思想，即我们运用正确性有保证的方法，最终得到的结果是这样一个性质。而题解区做法是首先令这一条件成立，再根据得到的线性方程组，使用 exgcd 和一些数学推导求解。这也体现了 exgcd 与辗转相除的本质联系。

不妨设对于向量 \(a, b\)，我们要将 \(x_b\) 变为 \(0\)。此时 \(x_{a'}\) 已经确定，即 \(\gcd(x_a, x_b)\)。因此，对于方程 \(xx_a + yx_b = \gcd(x_a, x_b)\)，容易用 扩展欧几里得 算法求得一组解，则 \(y_{a'} = xy_a + yy_b\)。这是因为 \(a' = xa + yb\)。对于向量 \(b'\)，有 \(x_{b'} = 0\)，因此有线性方程组

\[\begin{cases} xx_a + yx_b = 0 \\ xy_a + yy_b = y_{b'} \end{cases} \]

注意该方程组的 \(x, y\) 与之前 exgcd 求得的 \(x, y\) 不同。同时我们需使 \(y_{b'}\) 绝对值最小，否则可能出现 \(y_{b'} = 2\)，但 \((0, 1) \in \mathrm{span}(a, b)\) 的情况，即对于 \(\mathrm{span}(a, b)\) 中横坐标为 \(0\) 的所有点，\((0, y_{b'})\) 不是与 \((0, 0)\) 相邻的那一个，这样与 \((0, 0)\) 相邻的点无法表示。

根据第一个方程，得到 \(x, y\) 的关系式 \(y = \dfrac{-xx_a}{x_b}\)。带入第二个方程，得到 \(xy_a - \dfrac{xx_ay_b}{x_b} = y_{b'}\)，即

\[x\times \dfrac{y_ax_b - x_ay_b}{x_b} = y_{b'} \]

我们的目标很明确：找到 绝对值 最小的合法的 \(x\)。把 \(x\) 写成 \(\dfrac {x_b}d\) 的形式（因为分母是 \(x_b\)），那么 \(y = -\dfrac{x_a} d\)，因此 \(d\) 满足

\[\begin{cases} d \mid x_b \\ d \mid x_a \\ d \mid y_ax_b - x_ay_b \end{cases} \]

注意到若满足前两条限制，则第三条限制自动满足，故忽略。为使 \(x\) 的绝对值最小，\(d\) 的绝对值应尽量大。到这一步，大家应该都能看出 \(d\) 应取 \(\gcd(x_a, x_b)\)。因此，\(y_{b'} = \dfrac{y_ax_b - x_ay_b}{\gcd(x_a, x_b)}\)。

综上，我们将原向量 \(a, b\) 写成了另两个向量 \(a', b'\)，其中 \(x_{a'} = \gcd(x_a, y_a)\)，\(y_{a'}\) 用 exgcd 求解，\(x_{b'} = 0\)，\(y_{b'} = \dfrac{y_ax_b - x_ay_b}{\gcd(x_a, x_b)}\)。对 \(a, c\) 做一遍类似的操作，再合并 \(b, c\)（即类似线性代数解法，令 \(y_b \gets \gcd(y_b, y_c)\)，然后丢弃 \(c\)）即可。时间复杂度也是线性对数。

---

另一种求解 \(y_{b'}\) 的思路（来源于 TheLostWeak 的博客）：\(a', b'\) 可以整系数线性组合出 \(a, b\)，否则显然不满足条件，因为 \(a, b\in \mathrm{span}(a, b)\)。

根据上述性质，考虑 \(a'\)。由于 \(x_{a'} = \gcd(x_a, x_b)\)，所以为了使横坐标等于 \(x_a\)，需要为 \(a'\) 乘以 \(\dfrac{x_a}{\gcd(x_a, x_b)}\) 即 \(\dfrac{x_a}{x_{a'}}\) 的系数，得到 \(\left(x_a, \dfrac{x_ay_{a'}}{x_{a'}}\right)\)。由于我们可以通过向量 \(b' = (0, y_{b'})\) 得到 \((x_a, y_a)\)，因此 \(y_{b'} \left |\ y_a - \dfrac{x_ay_{a'}}{x_{a'}}\right.\) 。同理，\(y_{b'} \left |\ y_b - \dfrac{x_by_{a'}}{x_{a'}}\right.\)。故

\[y_{b'} = \gcd\left(\dfrac{y_ax_{a'} - x_a y_{a'}}{x_{a'}}, \dfrac{y_bx_{a'} - x_by_{a'}}{x_{a'}}\right) \]

易证若 \(y_{b'}\) 小于上述 \(\gcd\)，将导致存在 \(p\in \mathrm{span}(a', b')\)，\(p\notin \mathrm{span}(a, b)\)。若 \(y_{b'}\) 大于上述 \(\gcd\)，\(a', b'\) 无法整系数线性组合出 \(a, b\) 中的至少一个。

联立后两种方法描述 \(y_{b'}\) 的式子，稍作化简后得到等式 \(y_ax_b - x_ay_b = \gcd(y_ax_{a'} - x_a y_{a'}, {y_bx_{a'} - x_by_{a'}})\)。这也许说明了某些性质，但笔者已经不想研究了 QAQ，感兴趣的读者可自行钻研。

*VI. P3518 [POI2011]SEJ-Strongbox

若 \(v\) 在群里，则所有 \(\leq n\) 且是 \(\gcd(v, n)\) 的倍数的数也在群里。这是因为 \(kv \bmod n\) 取到了所有这样的数。证明：设 \(d = \gcd(v, n)\)，\(d\mid t\) 且 \(t\) 不在群里，这意味着 \(kv \equiv t\pmod n\) 即 \(kv + yn \equiv t \pmod n\) 无解，根据裴蜀定理，它等价于 \(\gcd(v, n) \nmid t\) 即 \(d\nmid t\)，矛盾。证毕。

因此，考虑枚举这个 \(d = \gcd(v, n)\)，若合法则答案即 \(\max\dfrac n d\)，即我们需要找到最小的合法的 \(d\)。

如何判断合法：不妨设 \(d_i = \gcd(m_i, n)\)，\(d\) 首先得是密码与 \(n\) 的 \(\gcd\) 即 \(d_k\) 的因数，其次任何 \(d_i(1\leq i < k)\) 不能是 \(d\) 的倍数。

考虑后者限制：给所有 \(d_i(1\leq i < k)\) 打上标记，从大到小枚举 \(n\) 的每个因数 \(c\)，若 \(c\) 被打上标记，则 \(\dfrac{c}{p_j}\) 也应被打上标记（其中 \(p_j\) 表示能整除 \(c\) 的 \(n\) 的质因子），表示若 \(c\) 是某个 \(d_i(1 \leq i < k)\) 的因数，则 \(\dfrac c {p_j}\) 显然也是。

剩下来没有被打上标记的所有 \(n\) 的因数 \(d\)，若 \(d\) 能被 \(d_k\) 整除则合法。找到最小的这样的 \(d\)，则答案为 \(\dfrac n d\)。

打标记的过程用哈希表实现，时间复杂度 \(\mathcal{O}(\sqrt n + k\log n + d(n)\omega(n))\)。\(\omega(i)\) 表示 \(i\)​ 的质因数个数。

*VII. P7325 [WC2021] 斐波那契

首先我们需要这样的事实：普通斐波那契数列在模 \(m\) 意义下纯循环，且循环节长度为 \(\mathcal{O}(m)\)。证明过于复杂，略去，读者可当作结论背诵。

\(F_0 = a\)，\(F_1 = b\) 的第 \(p\) 项等于 \(af_{p - 1} + bf_p\)，独立 \(a, b\) 前的系数可得该结果。

首先特判 \(a, b = 0\) 的情况。

令 \(b = -b\)，则问题等价于

\[af_{p - 1} \equiv bf_p\pmod m \]

自然，我们希望将 \(b\) 移到方程左侧，\(f_{p - 1}\) 移到方程右侧，这样可以直接预处理所有 \(\dfrac {f_p}{f_{p - 1}}\) 的值。但是 \(m\) 并不是质数，因此需要化简。

• 化简使用的核心思路是，同余方程 \(A \equiv B\pmod m\) 等价于 \(\dfrac A d \equiv \dfrac B d \pmod {\dfrac m d}\)，其中 \(A, B\) 均为代数式，\(d \mid A, B, m\)。直观理解很显然，感性说明就是 \(d\) 在该同余方程中完全没有起到任何作用。

令 \(d = \gcd(a, b, m)\)，等式两侧同时除以 \(d\)，得到

\[\dfrac a d f_{p - 1} \equiv \dfrac b d f_p\pmod {\dfrac m d} \]

欲将等式两侧同时除以 \(\dfrac b d\)，即保证 \(\dfrac b d\) 在模 \(\dfrac m d\) 意义下有逆元，则需 \(\dfrac b d \perp\dfrac m d\)。但并不一定满足。

令 \(d' = \gcd\left(\dfrac b d, \dfrac m d\right)\)。根据既约性，\(d'\perp a\)，因此必然有 \(d'\mid f_{p - 1}\)，因为方程右侧是 \(d'\) 的倍数。因此，

\[\dfrac a d \dfrac{f_{p - 1}}{d'} \equiv \dfrac b {dd'} f_p\pmod {\dfrac m {dd'}} \]

此时可以将 \(b\) 除过去了。

\[\dfrac a d \left(\dfrac b {dd'} \right) ^ {-1}\dfrac{f_{p - 1}}{d'} \equiv f_p\pmod {\dfrac m {dd'}} \]

欲将等式两侧同时除以 \(\dfrac{f_{p - 1}}{d'}\)，需满足 \(\dfrac{f_{p - 1}}{d'} \perp \dfrac {m}{dd'}\)，因为斐波那契数列的性质 \(f_p \perp f_{p - 1}\)，而等式右侧必须是 \(\gcd\left(\dfrac{f_{p - 1}}{d'}, \dfrac {m}{dd'}\right)\) 的倍数，这意味着这个 \(\gcd\) 只能等于 \(1\)。

上述推导过程说明我们需要枚举 \(d, d'\) 和 \(p\)，并将 \(\left(d, d', \dfrac {f_p}{\dfrac {f_{p - 1}}{d'}} \bmod \dfrac {m}{dd'}\right)\) 作为三元组塞入 map 方便查询。根据一开始的结论，复杂度是 \(m\) 的所有因数的因数和，再乘以 map 的 \(\log\)，无法承受。此时需要利用使得方程有解时这三个变量必须满足的性质降低复杂度。

注意到 \(d'\mid f_{p - 1}\) 且 \(\dfrac {f_{p - 1}}{d'} \perp \dfrac {m}{dd'}\)，这说明枚举 \(d, p\) 之后，\(d'\) 只能等于 \(\gcd\left(f_{p - 1}, \dfrac m d\right)\)。即 \(d'\) 不需要枚举，它随着 \(d, p\) 的确定而确定。这样复杂度变成 \(\mathcal{O}(\sigma(m))\) 即 \(m\) 的约数个数和，大约是 \(m \log \log m\) 量级（证明详见 p7325 - ycx's blog），因此总复杂度即 \(\mathcal{O}((m\log\log m + n) \log m)\)。

• 注意，当 \(f_p\) 或 \(f_{p - 1}\) 等于 \(0\) 时，直接忽略，因为 \(f_p\) 和 \(f_{p - 1}\) 不可能同时为 \(0\)，因此等式两侧有一处非零，一处为零（\(a, b = 0\) 的情况已经特判掉了），矛盾。

总结一下，我们在整个化简过程中，假设了 \(d\) 和 \(d'\) 两个仅与 \(a, b, m\) 有关的变量，因此预处理时需要枚举 \(d\) 和 \(d'\)。但根据方程有解时 \(d\) 和 \(d’\)​ 所具有的性质，我们得以降低复杂度。这种思想方法（在回答多组询问时，为了解决问题，需要设和询问参数相关的变量，那么在预处理时枚举这些变量的所有情况，即可考虑到给定询问参数的所有情况）是很巧妙的，读者需仔细体会。

代码。

2. 欧拉函数

欧拉函数是一类非常重要的数论函数。

2.1 定义与性质

欧拉函数定义为在 \([1, n]\) 中与 \(n\) 互质的整数的个数，记作 \(\varphi(n)\) 。

性质 1：若 \(p\) 为质数，则 \(\varphi(p ^ k) = (p - 1) \times p ^ {k - 1}\)。

证明：在 \([1, p ^ k]\) 中所有不是 \(p\) 的倍数的数都与 \(p ^ k\) 互质。因此 \(\varphi(p ^ k) = p ^ k - p ^ {k - 1} = (p - 1)p ^ {k - 1}\)，或者写成 \(p ^ k \times \dfrac{p - 1}{p}\)。得证。

性质 2（积性）：\(\varphi\) 是 积性函数。即若 \(a \perp b\)，则 \(\varphi(ab) = \varphi(a)\times \varphi(b)\)。

证明：设与 \(a\) 互质的数为 \(\{a_1, a_2, \cdots, a_{\varphi(a)}\}\)，那么在 \([1, ab]\) 内与 \(a\) 互质的整数可以表示为 \(i \times a + a_j(0\leq i < b,1\leq j \leq \varphi(a))\)。

因为 \(a \perp b\)，所以 \(ia(0 \leq i < b)\) 在模 \(b\) 意义下互不相同（1.4 节性质 4），即对于每一个 \(a_j\)，\(\{i \times a + a_j\}(0\leq i < b)\) 均构成 \(b\) 的完全剩余系 \(\{\overline 0, \overline 1, \cdots, \overline{b - 1}\}\)，即随着 \(i\) 从 \(0\) 变为 \(b - 1\)，\(i\times a + a_j\) 模 \(b\) 的余数取遍 \(0\sim b - 1\)。

因此，对于每一个 \(a_j\)，满足 \(b\perp i\times a + a_j\) 的 \(i\) 的个数为 \(\varphi(b)\)。因此，与 \(ab\) 互质的数的个数为 \(\varphi(ab) = \varphi(a) \times \varphi(b)\)，即 \(\varphi\) 为积性函数。得证。

性质 3（计算式）：根据算数基本定理，设 \(n\) 被唯一分解为 \(\prod\limits_{i = 1} ^ m p_i ^ {c_i}\)，则 \(\varphi(n) = n \times \prod\limits_{i = 1} ^ m \dfrac{p_i - 1} {p_i}\)。

证明：根据性质 1 和性质 2，

\[\varphi(n) = \prod\limits_{i = 1} ^ m \varphi(p_i ^ k) = \prod\limits_{i = 1} ^ m p ^ k \times \dfrac{p_i-1}{p_i} = n \times \prod\limits_{i = 1} ^ m \dfrac{p_i - 1}{p_i} \]

得证。这是求解 \(\varphi(n)\) 的常用方法。

这个性质也可以通过 容斥原理 证明，而不需要性质 1，2。考虑去掉所有被至少一个 \(n\) 的质因子整除的数，再加上至少被两个 \(n\) 的质因子整除的数，以此类推，最终可以得到式子 \(\varphi(n) = n \times \sum\limits_S \dfrac {(-1) ^ {|S|}}{\prod_{p\in S} p}\)，其中 \(S\) 是 \(n\) 的质因子集合的子集。容易证明其等于 \(n \times \prod\limits_{p_i} \left(1 - \dfrac 1 {p_i} \right)\)。

这样可以反推出性质 2：设 \(a = \prod\limits_{i = 1} ^ {m_1} {p_i} ^ {c_i}\)，\(b = \prod\limits_{i = 1} ^ {m_2} {q_i} ^ {d_i}\)。由于 \(a \perp b\)，所以 \(p_i,q_i\) 互不相同。因此 \(ab = \prod\limits_{i = 1} ^ {m_1} {p_i} ^ {c_i} \times \prod\limits_{i = 1} ^ {m_2} {q_i} ^ {d_i}\)，即

\[\varphi(ab) = ab\times \prod\limits_{i = 1} ^ {m_1} \dfrac{p_i - 1} {p_i} \times \prod\limits_{i = 1} ^ {m_2} \dfrac{q_i - 1}{q_i} = \varphi(a) \times \varphi(b) \]

int phi(int x) {
	int ans = x;
	for(int i = 2; i * i <= x; i++)
		if(x % i == 0) {
			while(x % i == 0) x /= i;
			ans = ans / i * (i - 1);
		}
	return ans / x * max(1, x - 1);
}

性质 4：若 \(p\) 为质数，则 \(\varphi(p) = p - 1\)。

证明：根据质数的定义可知 \(i \perp p(1 \leq i < p)\)，故 \(\varphi(p) = p-1\)。

性质 5：若 \(a \mid b\)，则 \(\varphi(ab) = a \times \varphi(b)\)。
证明：对比 \(\varphi(ab)\) 与 \(\varphi(b)\) 的公式，因为 \(a \mid b\)，所以 \(\prod\limits_{i = 1} ^ m \dfrac{p_i - 1}{p_i}\) 是相同的，只是左边的 \(b\) 变成了 \(ab\)。故 \(\varphi(ab) = a \times \varphi(b)\)。

• 直观理解：因为 \(ab\) 相较于 \(b\) 并没有增加更多质因子，所以原来与 \(b\) 互质的数仍然与 \(ab\) 互质，而 \([1, ab]\) 当中与 \(b\) 互质的数的个数显然为 \(a \varphi(b)\)，因为一个与 \(b\) 互质的数加上 \(kb(k\in \Z)\) 后仍然与 \(b\) 互质。

性质 6（线性筛欧拉函数）：若 \(p\) 为质数且 \(p\mid n\)，则

\[\varphi(p) = \begin{cases} p \times \varphi(\frac n p) \quad & (p ^ 2 \mid n) \\ (p - 1) \times \varphi(\frac n p) & (p ^ 2 \nmid n) \end{cases} \]

由性质 1，4，5 可得。这一性质是线性筛欧拉函数的关键结论。

性质 7（欧拉反演）：\(\sum\limits_{d\mid n} \varphi(d) = n\)。

证明：令 \(i\) 是 \(1\sim n\) 的整数，\(d = \gcd(i, n)\)，则 \(\dfrac i d \perp \dfrac n d\)。根据这一点，使得 \(\gcd(i, n) = d\) 的 \(i\) 的个数即 \(\varphi \left(\dfrac n d \right)\)。因为 \(\gcd(i, n) \in [1, n]\)，则

\[n = \sum\limits_{d \mid n} \sum\limits_{i = 1} ^ n[\gcd(i, n) = d] = \sum\limits_{d\mid n} \varphi\left(\dfrac n d\right) = \sum\limits_{d\mid n} \varphi(d) \]

得证。如果读者了解狄利克雷卷积，会发现这是 \(1 * \varphi = \mathrm{id}\)。

性质 8：\(2 \mid \varphi(n) (n > 2)\)。证明：若 \(x \perp n\)，则 \(n - x\perp n\)，故所有小于 \(n\) 且与 \(n\) 互质的数能一一配对。一个特例是 \(x = n - x\) 时，此时 \(x = \dfrac n 2\)，\(\gcd(x,n) = x \neq 1\)。得证。

性质 9：若 \(a \mid b\)，则 \(\varphi(a) \mid \varphi(b)\)。根据欧拉定理的计算式易证。

性质 10：使得 \(\gcd(n, x) = d\) 且 \(1\leq x \leq n\) 的 \(x\) 的个数为 \(\varphi\left(\dfrac n d\right)\)。

证明：容易证明 \(\gcd(n, x) = d\) 的充分必要条件为 \(\dfrac n d \perp \dfrac x d\)。因为 \(1\leq x \leq n\)，所以 \(1\leq \dfrac x d \leq \dfrac n d\)。因此合法的 \(\dfrac x d\) 的个数为 \(\varphi\left(\dfrac n d\right)\)。得证。

将 \(x\) 的限制改为 \(0\leq x < n\)，命题仍成立。因为在模 \(n\) 意义下 \(0\) 等于 \(n\)，或者理解为 \(\gcd(n, n) = \gcd(0, n) = n\)。

• 简单地说，首先显然 \(x\) 得是 \(d\) 的倍数，其次 \(\dfrac x d\) 不能和 \(\dfrac n d\) 有公因子，否则 \(\gcd(x, n)\) 就会大于 \(d\)。

2.2 欧拉定理

回顾费马小定理的证明过程，我们发现不需要 \(p\) 是质数这一条件，当 \(a \perp p\) 时 \(ax\bmod p\) 即互不相同。

同时我们知道，两个模 \(p\) 互质的数相乘后仍与 \(p\) 互质，因此，我们尝试将费马小定理扩展至更一般的情况。

为了防止出现乘积等于零的情况，我们将研究目标设为 \(p\) 的 简化剩余系 而非完全剩余系。

设 \(S=\{p_1,p_2,\cdots,p_{\varphi(p)}\}\) 为 \(p\) 的简化剩余系，即所有与 \(p\) 互质且模 \(p\) 互不相同的数组成的集合。对于任意 \(p_i, p_j\)，若 \(i \neq j\)，则根据上述分析，\(ap_i\) 与 \(ap_j\) 在模 \(p\) 意义下的余数不相等且仍与 \(p\) 互质。

因此在模 \(p\) 意义下，\(S\) 中每个数乘以 \(a\) 后仍与 \(S\) 相等。故 \(\prod\limits_{i = 1} ^ {\varphi(p)} p_i \equiv \prod\limits_{i = 1} ^ {\varphi(p)} ap_i\pmod p\)。显然 \(\prod p_i\perp p\)。等式两边同时除以 \(\prod\limits_{i = 1} ^ {\varphi(p)} p_i\) 得到

\[a ^ {\varphi(p)} \equiv 1 \pmod p \]

在计算与模数互质的某个数的幂时，指数可以对模数的欧拉函数取模。可以用来化简公式或减小常数（前提是模数是定值或其欧拉函数容易求得）。

扩展欧拉定理：欧拉定理的扩展版本，如下。

\[a ^ b \equiv \begin{cases} a ^ {b\ \bmod\ \varphi(p)} & \gcd(a,p) = 1 \\ a ^ b & \gcd(a, p) \neq 1, b < \varphi(p) \\ a ^ {b\ \bmod\ \varphi(p) + \varphi(p)} & \gcd(a, p)\neq 1, b \geq \varphi(p) \end{cases} \pmod p \]

感性证明：当 \(\gcd(a, p) \neq 1\) 时，不断乘以 \(a\) 会让 \(a ^ i\) 和 \(p\) 的 \(\gcd\) 不断变大，直到某个特定的 \(a ^ r\) 之后 \(\gcd\) 不再变化，因为此时 \(\gcd(a ^ r, p)\) 受到 \(p\) 的每个与 \(a\) 相同的质因子的次数的限制。令这个 \(\gcd\) 为 \(d\)，考虑 \(a ^ r \bmod p, a ^ {r + 1} \bmod p, \cdots\)，显然它们均为 \(d\) 的倍数，且除以 \(d\) 之后会取遍所有与 \(\dfrac p d\) 互质的数，这是因为 \(a \perp \dfrac p d\)。根据欧拉定理，\(a ^ k \bmod {\dfrac p d}\) 有循环节 \(\varphi \left(\dfrac p d \right)\)，因此 \(\left(a ^ k \bmod {\dfrac p d} \right)\times d\) 即 \(a ^ k \bmod p\) 也有循环节 \(\varphi \left(\dfrac p d \right)\)。故从 \(a ^ r\) 开始，\(a ^ {r + k} \bmod p\) 有循环节 \(\varphi(p)\)。

严谨证明 摘自 OI wiki，如下。

对于 \(a\) 的 \(i\) 次幂模 \(p\) 构成的无穷序列 \(a ^ 0, a ^ 1, \cdots\)，必然存在循环节的开始位置 \(r\) 和循环节长度 \(s\)，使得 \(a ^ i\) 从 \(r\) 开始以 \(s\) 为循环节长度循环，即对于任意 \(i \geq r\) 满足 \(a ^ i \equiv a ^ {i + s}\)。欲证扩展欧拉定理，可证 \(r \leq \varphi(p)\) 且 \(s\mid \varphi(p)\)。

当 \(a\) 是质数时，令 \(p'\) 为 \(p\) 去掉所有质因子 \(a\) 后的结果，\(p = a ^ r p'\)。此时 \(a \perp p'\)，显然 \(\varphi(p') \mid \varphi(p)\)（\(p\) 是 \(p'\) 的倍数）。因为 \(a ^ {\varphi(p')} \equiv 1 \pmod {p'}\)，故 \(a ^ {\varphi(p)} \equiv 1 \pmod {p'}\)，故 \(a ^ {\varphi(p) + r} \equiv a ^ r \pmod {p}\)。因为 \(\varphi(p) = a ^ {r - 1}(a - 1) \varphi(p') \geq a ^ {r - 1}(a - 1) \geq r\)，得证。

当 \(a\) 是质数的 \(k\) 次幂时，令 \(a = q ^ k\)，\(p = q ^ r p'\)。由上一条，\(q ^ {\varphi(p)} \equiv 1 \pmod {p'}\)。因此 \(q ^ {k\varphi(p)} \equiv 1 \pmod {p'}\)，即 \(a ^ {\varphi(p)} \equiv 1 \pmod {p'}\)。考虑令 \(r' = \left\lceil \dfrac r k \right\rceil\)，由于 \(q ^ {k\varphi(p) + r} \equiv q ^ r\pmod p\)，且 \(r'k \geq r\)，所以 \(q ^ {k\varphi(p) + r'k} \equiv q ^ {r'k}\pmod p\)，即 \(a ^ {\varphi(p) + r'} \equiv a ^ {r'} \pmod p\)。因为 \(r' \leq r\)，所以由上一条，\(r' \leq \varphi(p)\)，得证。

当 \(a = q_1 ^ {k_1} q_2 ^ {k_2}\) 时，因为 \(q_1 ^ {k_1\varphi(p)} \equiv 1 \pmod {p'}\) 且 \(q_2 ^ {k_2\varphi(p)} \equiv 1 \pmod {p'}\)，所以 \(a ^ {\varphi(p)} \equiv \pmod {p'}\)。如法炮制，令 \(r' = \max\left(\left\lceil \dfrac {r_1} {k_1} \right\rceil, \left\lceil \dfrac {r_2} {k_2} \right\rceil \right)\)，容易证明 \(a ^ {\varphi(p) + r'} \equiv a ^ {r'} \pmod {p'}\) 且 \(r' \leq \max(r_i) \leq \varphi(p)\)，得证。

当 \(a\) 为多个质数的乘积时，可以利用上一条类似证明。扩展欧拉定理得证。

扩展欧拉定理的应用见例 IV, V.

2.3 线性筛欧拉函数

根据欧拉函数的性质 6，我们可以线性筛出所有数的欧拉函数。关于线性筛，见 各类反演与狄利克雷卷积 第六章线性筛部分。

初始化 \(\varphi(1) = 1\)。对于每个质数 \(p\)，\(\varphi(p) = p - 1\)。枚举所有数 \(i\) 并遍历所有筛到的素数 \(pr_j\)。若 \(pr_j\nmid i\)，则 \(\varphi(i \times pr_j) = (pr_j - 1) \times \varphi(i)\)。否则 \(\varphi(i \times pr_j) = pr_j \times \varphi(i)\)，同时根据线性筛的算法，此时应退出遍历。

int cnt, pr[N], phi[N], vis[N];
void sieve() {
	phi[1] = 1;
	for(int i = 2; i < N; i++) {
		if(!vis[i]) pr[++cnt] = i, phi[i] = i - 1;
		for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
			vis[i * pr[j]] = 1, phi[i * pr[j]] = (pr[j] - 1) * phi[i];
			if(i % pr[j] == 0) {phi[i * pr[j]] = pr[j] * phi[i]; break;}
		}
	}
}

2.4 例题 I. SP4141 ETF - Euler Totient Function

欧拉函数模板题。

II. UVA10179 Irreducable Basic Fractions

根据既约分数 \(\dfrac m n\) 的定义 \(m \perp n\) 且 \(0 \leq m < n\) 可知答案即 \(\varphi(n)\)。

III. UVA11327 Enumerating Rational Numbers

本题是上题的变形。样例告诉我们分母不大于 \(2\times 10^5\)。因此预处理出 \([1,2\times 10^5]\) 每个数的欧拉函数。从小到大枚举分母，求出分母后再根据剩余个数从小到大枚举分子。

*IV. P4139 上帝与集合的正确用法

题意简述：求 \(2 ^ {2 ^ {2 ^ {2 ^ {2 ^ {\cdots}}}}} \bmod p\)，\(1 \leq p \leq 10 ^ 7\)。

初看这个无限幂塔读者可能摸不着头脑，因为直觉告诉我们这个值不存在，就好像 \(\infty\) 是一个不确定的数一样。但反直觉的是当 \(x\) 足够大时，\(2\uparrow\uparrow x\) 与 \(2\uparrow\uparrow (x+1)\) 在模 \(p\) 意义下相同。\(\uparrow\) 见 高德纳箭号表示法。

为什么呢？根据扩展欧拉定理，上面的幂塔等于 \(2^{2^{2^{2^{\cdots}}}\bmod \varphi(p)+\varphi(p)}\bmod p\)，不断使用扩展欧拉定理得到

\[\large 2 ^ {2 ^ {2 ^ {2 ^ {\cdots} \bmod \varphi(\varphi(\varphi(p))) +\varphi(\varphi(\varphi(p)))} \bmod \varphi(\varphi(p)) + \varphi(\varphi(p))} \bmod \varphi(p) + \varphi(p)} \bmod p \]

因为幂指数无穷叠加，所以不需要担心出现 \(2^{2^{2^{\cdots}}}<\varphi(p)\) 导致扩展欧拉定理失效，可以递归实现。

又因为 \(2\mid \varphi(n)\) 且 \(\varphi(2n)\leq n\)，所以 \(\varphi(p)\) 的迭代值会以指数方式减小为 \(1\)。此时不用关心继续往上的幂次是多少了，因为任何数模 \(1\) 都得 \(0\)，这是终止条件。综上，线性筛出 \(p\) 以内所有数的欧拉函数即可做到时间复杂度 \(\mathcal{O}(p+T\log p)\)。每次直接暴力算 \(\varphi(p)\) \(\mathcal{O}(T\sqrt p\log p)\) 也可以通过。

int F(int x) {
	if(x <= 2) return 0; int v = phi(x); 
	return ksm(2, F(v) + v, x); // 2 ^ {F(v) + v} % x
}

*V. P3747 [六省联考 2017] 相逢是问候

根据上一题的结论，\(c ^ {c ^ {c ^ {\cdots ^ {a_i}}}} \bmod p\) 在迭代次数足够多时为定值：迭代次数 \(cnt\) 为使得 \(\varphi(\varphi(\cdots\varphi(\varphi(p))\cdots)) = 1\) 的迭代次数，为 \(\log p\) 级别。

预处理出每个数迭代 \(i\) 次后的结果，即对每个位置预处理幂塔迭代 \(1\sim cnt\) 次 \(c\) 之后的结果（不是 \(cnt - 1\)，因为最顶上的模 \(1\) 的数是 \(a_i\) 而不是 \(c\)），然后对每个线段树上的叶子结点记录操作次数最小值 \(d_i\)，如果还有可以操作的区间即 \(d_i<cnt\) 则递归下去暴力修改。

此外，判断指数是否大于等于 \(p\) 可以在快速幂时实现：乘完先不取模，如果值不小于模数再记录并取模。这部分比较细节，需要多加注意。

时间复杂度是 \(\mathcal{O}(n\log n\log^2 p)\) ：欧拉函数有 \(\log p\) 种，线段树上 \(n\) 个位置每种欧拉函数递归 \(\log p\) 层，每次修改都要快速幂。注意到只有 \(\log p\) 种模数，所以可把快速幂换为光速幂。时间复杂度 \(\mathcal{O}(n\log^2 p)\)。代码。

3. 离散对数问题

离散对数问题即在模 \(p\) 意义下求解 \(\log_a b\)。这等价于求解离散对数方程

\[a ^ x \equiv b \pmod p \]

其中 \(x\) 即 \(\log_a b\)。模 \(p\) 意义下的 \(\log_a b\) 可能不存在，也可能存在多个，我们的目标是找到任意一个。

当 \(a, p\) 互质时，我们可以使用大步小步算法求解。当 \(a, p\) 不互质时，可以使用扩展大步小步算法求解。

3.1 大步小步算法

大步小步算法全称 Baby Step, Giant Step，简称 BSGS。普通 BSGS 适用于 \(a\perp p\) 的情况。

大步小步算法运用了 根号平衡（或称为 meet-in-the-middle）的技巧：设块长为 \(M\) 且 \(x = AM - B(0\leq B < M)\)，则有 \(a ^ {AM} \equiv ba ^ B \pmod p\)。直接枚举 \(a ^ {AM}\) 与 \(ba ^ B\) 所有可能的取值并通过哈希表（pb_ds 的 gp_hash_table <int, int>）判断是否相等，即可 \(\mathcal{O}(\max(A, B))\) 求出 \(x\)。注意到 \(0\leq B < M, 0\leq A\leq \lceil\frac{p - 1} M \rceil\)（根据欧拉定理，若 \(x\) 有解，则必然存在解在 \([0, p - 2]\) 范围内），将块长 \(M\) 设为 \(\lceil\sqrt{p}\rceil\) 即可取到最优复杂度 \(\mathcal{O}(\sqrt{p})\)。

int BSGS(int a, int b, int p) {
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	for(int i = 1; i <= B; i++) mp[1ll * (A = 1ll * A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; i++, AA = 1ll * AA * A % p)
		if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
} 

容易发现 BSGS 求得的是 \(\log_a b\) 的最小的非负整数解，因为我们从小到大枚举指数。

关于 \(\log_a b\) 即使得 \(a ^ x \equiv b \pmod p\) 成立的 \(x\) 的循环节长度，详见 6.1 阶。

3.2 扩展大步小步算法

对于更加 general 的离散对数方程 \(a^x\equiv b\pmod p\)，如果没有 \(a\perp p\) 该怎么办呢？

核心思想是从已知到未知：既然有了可以解决 \(a\perp p\) 的 BSGS，那么我们尝试把 \(a,p\) 凑成互质。如果给等式两边同时除以 \(d = \gcd(a, p)\)，则方程变为 \(\dfrac a d a ^ {x - 1} \equiv \dfrac b d \pmod{\dfrac p d}\)。若 \(d \nmid b\) 显然无解。

注意到 \(\dfrac a d \perp \dfrac p d\)，因此前者在模后者意义下存在逆元。但因为 \(p\) 可能不是质数，故需 exgcd 求解逆元。移项，方程变为 \(a ^ {x - 1} \equiv \dfrac b d \times \left(\dfrac a d \right) ^ {-1} \pmod {\dfrac p d}\)，等式右边可视作常数。

因为 \(a\) 与 \(\dfrac p {\gcd(a, p)}\) 可能不互质，如 \(a = 2\)，\(p = 4\)，故重复上述操作直到 \(a, p\) 互质，此时直接使用 BSGS 求解即可。

设提出的 \(a\) 的个数为 \(k\)，即 \(\gcd(a, p) \neq 1\) 时上述操作的次数，则求得的解还应加上 \(k\)。注意在每一次操作开始前特判 \(b = 1\)，此时答案等于 \(k\)。

时间复杂度 \(\mathcal{O}(\sqrt p + \log ^ 2 p)\)，分别是 BSGS 以及求 \(\log\) 次 \(\gcd\) 和乘法逆元的复杂度。代码见例题 III.

3.3 例题 I. P3846 [TJOI2007] 可爱的质数 /【模板】BSGS

BSGS 模板题。

II. P2485 [SDOI2011]计算器

操作 1 快速幂，操作 2 exGCD 求逆元，操作 3 BSGS。

III. SP3105 MOD - Power Modulo Inverted

exBSGS 模板题。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>

using namespace std;
using namespace __gnu_pbds;

int a, p, b;
void exgcd(int a, int b, int &x, int &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int inv(int x, int p) {return exgcd(x, p, x, *new int), (x % p + p) % p;}
int BSGS(int a, int b, int p) {
	a %= p, b %= p;
	int A = 1, B = sqrt(p) + 1;
	gp_hash_table <int, int> mp;
	for(int i = 1; i <= B; i++) mp[1ll * (A = 1ll * A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; i++, AA = 1ll * AA * A % p) if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
}
int exBSGS(int a, int b, int p) {
	int d = __gcd(a, p), cnt = 0;
	a %= p, b %= p;
	while(d > 1) {
		if(b == 1) return cnt;
		if(b % d) return -1;
		p /= d, b = 1ll * b / d * inv(a / d, p) % p;
		d = __gcd(p, a %= p), cnt++;
	}
	int ans = BSGS(a, b, p);
	return ~ans ? ans + cnt : -1;
}
int main() {
	cin >> a >> p >> b;
	while(a) {
		int ans = exBSGS(a, b, p);
		if(~ans) cout << ans << "\n";
		else puts("No Solution");
		cin >> a >> p >> b;
	}
	return 0;
}

IV. P3306 [SDOI2013] 随机数生成器

我们尝试用《具体数学》给出的方法推公式。不妨令下标左移一位，即题目中给出的数视作 \(x_0\)。

令 \(s_i = \dfrac{x_i} {a ^ i}\)，那么 \(a ^ i s_i = a ^ i s_{i - 1} + b\)，即 \(s_i = s_{i - 1} + \dfrac b{a ^ i}\)，同时 \(s_0 = x_0\)。不难发现 \(s_i = x_0 + \sum\limits_{j = 1} ^ i \dfrac b {a ^ j}\)，那么

\[\begin{aligned} x_i & = a ^ i s_i \\ & = a ^ i x_0 + b \sum_{j = 0} ^ {i - 1} a ^ j \\ & = a ^ i x_0 + b \dfrac {a ^ i - 1} {a - 1} \\ & = a ^ i \left(x_0 + \dfrac b {a - 1} \right) - \dfrac b {a - 1} \end{aligned} \]

是裸的 BSGS。注意特判 \(a = 0\) 和 \(a = 1\)。时间复杂度 \(\mathcal{O}(T\sqrt p)\)。

4. 线性同余方程组

前置知识：扩展欧几里得算法。

求解形如

\[\begin{cases} x \equiv a_1 \pmod {m_1} \\ x \equiv a_2 \pmod {m_2} \\ \cdots \\ x \equiv a_k \pmod {m_k} \end{cases} \]

的 线性同余方程组 是信息学竞赛的常见内容。线性同余方程组涉及方面十分广泛（从多模 NTT 到高次剩余），因为它可以处理模数不是质数的情况，或者合并问题中的循环节。

• Note：excrt 比 crt 更容易理解且适用范围更广泛，因此笔者在合并线性同余方程组时一般使用 excrt。

4.1 中国剩余定理

中国剩余定理全称 Chinese Remainder Theorem，简称 CRT。它用于求解 模数两两互质 的线性同余方程组，即对于任意 \(i \neq j\)，均有 \(m_i \perp m_j\)。

CRT 的大致思想是求出若干数，使得这些数依次满足某一个同余方程组，且在其它模数意义下均为 \(0\)。则这些数的和即为所求。

根据上述初步感知，我们令 \(M = \prod m_i\)，并尝试为每个同余方程构造 \(x_i \equiv a_i\pmod {m_i}\)，记为条件一；且对于 \(j \neq i\) 均有 \(x_i\equiv 0 \pmod {m_j}\)，记为条件二。我们将目光放在单个同余方程 \(x_i \equiv a_i \pmod {m_i}\) 上。

首先，为满足条件二，\(x_i\) 应为 \(\prod\limits_{j \neq i} m_j\) 即 \(\dfrac M {m_i}\) 的倍数。令其为 \(c_i\)。我们发现令 \(x_i\) 等于 \(a_i c_i\) 即可满足条件二。为满足条件一，我们发现 \(c_i\) 和 \(m_i\) 互质（题目条件可推得），因此只需为 \(c_i\) 再乘上其在模 \(m_i\) 意义下的逆元即可。令 \(d_i\) 为 \(c_i ^ {-1} \pmod {m_i}\)，则 \(x_i = a_ic_id_i\) 满足两个条件。注意，\(d_i\) 需要通过 exgcd 求解，因为 \(m_i\) 可能不是质数。

对每个模数均进行一遍上述流程，则 \(\sum a_ic_id_i\) 即为所求。时间复杂度线性对数。模板题代码见例题 I.

4.2 扩展中国剩余定理

扩展中国剩余定理简称 excrt。它用于求解 一般形式 的线性同余方程组。它和中国剩余定理在本质上没有任何联系，仅是求解的问题形式相同。

• 笔者认为 excrt 更简单一些。

当模数不互质时，考虑合并两个同余方程 \(x\equiv a_1\pmod {m_1}\) 和 \(x\equiv a_2\pmod {m_2}\)。因为 \(x\) 可以表示成 \(a_1+pm_1\)，所以 \(a_1+pm_1\equiv a_2\pmod {m_2}\)，即 \(pm_1+qm_2\equiv a_2-a_1\pmod {m_2}\)，exgcd 求解即可（或者可以理解为 \(p \equiv \dfrac {a_2 - a_1}{m_1} \pmod {m_2}\) 用 exgcd 求逆元，两种方法本质相同）。合并后的方程即 \(x\equiv a_1+pm_1\pmod {\mathrm{lcm}(m_1,m_2)}\)。

根据裴蜀定理，若 \(\gcd(m_1,m_2)\nmid a_2-a_1\)，则方程组无解。时间复杂度线性对数，模板题代码见例题 II.

• 记得考虑 exgcd 解出来是负数的情况。在得到解之后需要进行取模。

4.3 例题 I. P1495 【模板】中国剩余定理(CRT)/曹冲养猪

中国剩余定理模板题。注意要使用 int128 或慢速乘。

#include <bits/stdc++.h>
using namespace std;

const int N = 10 + 5;
int n, a[N], b[N];
long long M = 1, ans;
void exgcd(int a, int b, int &x, int &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int inv(int x, int p) {return exgcd(x, p, x, *new int), (x % p + p) % p;}
int main() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i] >> b[i], M *= a[i];
	for(int i = 1; i <= n; i++) ans = (ans + (__int128)b[i] * (M / a[i]) * inv(M / a[i] % a[i], a[i])) % M;
	cout << ans << endl;
	return 0;
}

II. P4777 【模板】扩展中国剩余定理（EXCRT）

excrt 模板题。

#include <bits/stdc++.h>
using namespace std;

long long n, a, b, c, d;
void exgcd(long long a, long long b, long long &x, long long &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int main() {
	cin >> n >> a >> b;
	for(int i = 1; i < n; i++) {
		cin >> c >> d;
		long long e = __gcd(a, c), f = (d - b % c + c) % c, inv;
		c /= e, f /= e;
		exgcd(a / e, c, inv, *new long long), inv = (inv % c + c) % c;
		b += (__int128)f * inv % c * a, a *= c, b %= a;
	}
	cout << b << endl;
	return 0;
}

III. P4774 [NOI2018] 屠龙勇士

设第 \(i\) 次选用的剑的攻击力为 \(c_i\)，可以通过 multiset 模拟确定。问题转化为找到最小的 \(x\) 使得对于所有 \(i\) 都有 \(c_ix\equiv a_i\pmod {p_i}\) 且 \(c_ix\geq p_i\)。

先求出 \(d_i=\gcd(c_i,p_i)\)，若 \(d_i\nmid a_i\) 则无解，否则将 \(a_i,c_i,p_i\) 同时除以 \(d_i\)，此时有 \((c_i,p_i)=1\)，把 \(c_i\) 除过去就是标准的线性同余方程组。excrt 求解得到 \(x\)。

为满足第二个条件，我们可以先求出 \(e_i = \left \lceil \dfrac {a_i} {c_i} \right \rceil\) 表示打败 Boss \(i\) 至少要多少次攻击。若最终求得的 \(x < \max e_i\)，那么需将 \(x\) 加上 \(\left \lceil \dfrac {(\max e_i) - x} {p} \right \rceil \times p\)，其中 \(p\) 是最终的同余方程的模数。时间复杂度线性对数。代码。

IV. P4621 [COCI2012-2013#6] BAKTERIJE

细菌的运动情况会在不超过 \(4\times n^2=10^4\) 次后形成循环，因此先 BFS 找环，特判前 \(10^4\) 次运动，然后 \(4^k\) 枚举每个细菌进入 \((x,y)\) 时的方向，从而唯一确定一个线性方程组，excrt 即可。

时间复杂度 \(\mathcal{O}(4^kk\log V)\)，其中 \(V\) 是值域。由于每次添加的模数很小，只有 \(10^4\) 级别，可直接循环枚举。

V. P2480 [SDOI2010]古代猪文

求 \(g ^ {\sum\limits_{d\mid n} \binom n d}\bmod 999911659\)。指数对 \(999911658\) 取模，分解质因数后发现是 square-free number，直接 lucas + crt 即可。时间复杂度 \(d(n) \log n\)。

lucas 见第八章。

5. 数论分块

数论分块又称整除分块，因其解决的问题与整除密切相关而得名。具体地，数论分块用于求解形如

\[\sum_{i = 1} ^ n f(i) g\left(\left\lfloor\dfrac n i \right\rfloor\right) \]

的和式。前提是 \(f\) 的前缀和容易快速计算。

读者需要有这样的感性认知：使得 \(n\) 除以 \(x\) 下取整后等于 \(k\) 的正整数 \(x\) 的范围为 \(\left(\dfrac{n}{k + 1}, \dfrac n k \right] \cup \N_{+}\)，即 \(\left[\left\lfloor \dfrac n {k + 1}\right\rfloor + 1, \left\lfloor \dfrac n k\right\rfloor \right]\)。

5.1 算法介绍

部分摘自 OI wiki。

感性认知：当 \(i\) 较大时，\(i\) 的取值很多，但 \(\left\lfloor \dfrac {n} {i} \right\rfloor\) 被限制在较小的范围内，因此很多 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 均相同。

• 数论分块的时间复杂度基于以下引理（记作引理 5.1）：对于任意 \(n\in \N_+\) 以及 \(i\in [1, n]\)，不同的 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 至多 \(2\sqrt n\) 个。证明：当 \(i \leq \sqrt n\) 时，\(\left\lfloor \dfrac {n} {i}\right\rfloor\) 显然只有 \(\sqrt n\) 个。当 \(i \geq \sqrt n\) 时，\(\left\lfloor \dfrac {n} {i}\right\rfloor \leq \sqrt n\)，因此也只有 \(\sqrt n\) 个。证毕。

• 数论分块的正确性基于以下（记作引理 5.2）引理：\(\left\lfloor \dfrac {a} {bc}\right\rfloor = \left\lfloor \dfrac {\left\lfloor \frac {a} {b}\right\rfloor} {c}\right\rfloor\)。即先除以一个数，下取整后再除以一个数再下取整，等于除以这两个数的乘积后下取整。证明：令 \(a = db + r\)，则 \(\left\lfloor \dfrac {a} {bc}\right\rfloor = \left\lfloor \dfrac {d + \frac r b} {c}\right\rfloor\)。因为 \(0\leq \dfrac r b < 1\)，而 \(c, d\) 均为整数，所以 \(\dfrac r b\) 可忽略。证毕。

数论分块的结论如下：对于 \(i \in [1, n]\)，使得 \(\left\lfloor \dfrac {n} {i}\right\rfloor = \left\lfloor \dfrac {n} {j}\right\rfloor\) 的最大的 \(j\) 等于 \(\left\lfloor \dfrac {n} {\left\lfloor \frac {n} {i}\right\rfloor}\right\rfloor\)。显然 \(j\) 存在，因为 \(i\) 是 \(j\) 的一个合法取值。

感性证明：令 \(k = \left\lfloor \dfrac {n} {i}\right\rfloor\)，\(jk \leq n \Rightarrow j \leq \dfrac {n} {k}\)。因 \(j\) 是整数，故 \(j_{\max} = \left\lfloor \dfrac n k \right\rfloor\)。读者也可根据本章开头部分的感性认知来理解。

严谨证明：令 \(k = \left\lfloor \dfrac {n} {i}\right\rfloor\)，则 \(k \leq \dfrac n i\)。根据引理，\(\left\lfloor \dfrac {n} {k} \right\rfloor \geq \left\lfloor \dfrac {n} {\frac n i}\right\rfloor = i\)，所以 \(j\) 等于 \(i\) 的最大值即 \(\left\lfloor \dfrac {n} {k} \right\rfloor\)。若 \(j\) 还可以更大，即 \(\left\lfloor \dfrac {n} {j + 1}\right\rfloor = k\)，则 \(\left\lfloor \dfrac {\left\lfloor \frac {n} {j + 1}\right\rfloor} {k}\right\rfloor = 1\)，根据引理，即 \(\left\lfloor \dfrac {\left\lfloor \frac {n} {k}\right\rfloor} {j + 1}\right\rfloor = 1\)，即 \(\left\lfloor \dfrac {n} {k}\right\rfloor \geq j + 1\)。这和 \(\left\lfloor \dfrac {n} {i}\right\rfloor = j\) 矛盾。证毕。

通过上述分析，我们得到了数论分块算法的大致轮廓，如下所述。

设 \(s\) 为 \(f\) 的前缀和。\(l\) 从 \(1\) 开始，每次令 \(r \gets \left\lfloor\dfrac n {\left\lfloor\frac n l\right\rfloor}\right\rfloor\)，然后将答案加上 \((s(r) - s(l - 1)) \times g\left(\left\lfloor \dfrac {n} {i}\right\rfloor\right)\)。最后令 \(l\gets r+1\)，若大于 \(n\) 则退出。

根据引理 5.1，每个不同的 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 仅会被遍历一次，故时间复杂度 \(\mathcal{O}(\sqrt n)\)。

• 注意，当 \(i\) 的上界不等于 \(n\) 时，不妨设其为 \(m\)，则 \(r\) 应当与 \(m\) 取较小值（\(n > m\) 时会出现该情况），且当 \(\left\lfloor\dfrac n i\right\rfloor = 0\) 时需要特判，直接令 \(r\) 等于 \(m\)（\(n < m\) 时会出现该情况）。

5.2 扩展 5.2.1 向上取整

尝试将向下取整变为向上取整。

对于左边界 \(l\)，我们求出使得 \(\left\lceil\dfrac n l \right\rceil = \left\lceil\dfrac n r \right\rceil\) 的最大的 \(r\)。不妨设 \(k = \left\lceil\dfrac n l\right\rceil\)，则

\[r(k - 1) < n \Rightarrow r < \dfrac{n}{k - 1} \Rightarrow r\leq \dfrac{n-1}{k-1} \]

第二步转换是因为 \(n, k\) 均为正整数。上述推导类似向下取整时的感性证明部分。

因此，我们只需令 \(r\gets \left\lfloor\dfrac{n - 1}{\left\lceil\frac n l\right\rceil - 1}\right\rfloor\) 即可。

注意特判 \(\left\lceil\dfrac n l\right\rceil=1\) 的情况，此时 \(r\) 的上界为无穷大，需要与实际上界取较小值。

5.2.2 高维数论分块

当和式中出现若干下取整，形如

\[\sum_{i = 1} ^ n f(i) \prod_{j = 1} ^ c g\left(\left\lfloor \dfrac {n_j} {i}\right\rfloor\right) \]

时，只需稍作修改，令 \(r = \min\limits_{j = 1} ^ c\left(\left\lfloor \dfrac {n_j} {\left\lfloor \frac {n_j} {i}\right\rfloor}\right\rfloor\right)\) 即可。不要忘记对 \(n\) 取 \(\min\)。

时间复杂度为 \(\sum \sqrt {n_j}\)。将令 \(\left\lfloor \dfrac {n_j} {i}\right\rfloor \neq \left\lfloor \dfrac {n} {i + 1}\right\rfloor\) 的位置视作断点，则总共的断点数量为每个下取整式的端点数量相加（而非相乘），而我们只会在每个断点处遍历一次，故有该时间复杂度。

5.3 例题 I. 某模拟赛 你还没有卸载吗

给定 \(A_1, B_1, A_2, B_2, N\)，求有多少 \(x\in [1, N]\) 使得 \(B_1 + \left\lfloor\dfrac{A_1}{x}\right\rfloor = B_2 + \left\lfloor\dfrac{A_2}{x}\right\rfloor\)。\(T\leq 2\times 10 ^ 3\)，其他所有数 \(\in [1, 10 ^ 8]\)。时限 1s。

笔者尝试用数学方法推导答案，无果。故考虑数论分块固定 \(\dfrac{A_1} x\)，解出 \(d = \dfrac{A_2}{x}\)，从而反推出合法的 \(x\) 的范围：\([l, r] \cap \left[\dfrac{A_2}{d + 1} + 1, \dfrac{A_2}{d}\right]\)。时间复杂度 \(\mathcal{O}(T\sqrt V)\)。

另一种方法是直接二维数论分块。细节更少，且时间复杂度不变。

启示：当用数学手段推导公式无果时可以考虑固定一些变量。

#include <bits/stdc++.h>
using namespace std;
int T, a1, b1, a2, b2, n;
int main() {
	cin >> T;
	while(T--) {
		int ans = 0;
		cin >> a1 >> b1 >> a2 >> b2 >> n;
		for(int l = 1, r = 1; l <= n; l = r + 1) {
			r = min(n, min(a1 / l ? a1 / (a1 / l) : n, a2 / l ? a2 / (a2 / l) : n));
			if(b1 + a1 / l == b2 + a2 / l) ans += r - l + 1;
		}
		cout << ans << endl;
	}
	return 0;
}

II. *CF1603C. Extreme Extension

数论分块优化 DP。

一个数如何分裂由后面分裂出来的数的最小值决定，而显然我们一定是贪心使分出来的数尽量均匀，例如若 \(9\) 要裂成若干个比 \(4\) 小的数那么 \(3,3,3\) 就比 \(2,3,4\) 更优。

这启发我们从后往前考虑：对于每个数 \(a_i\) 和数值 \(j\in [1,a_i]\)，求出有多少个以 \(a_i\) 开头的子串使得分裂出的最小值为 \(j\)，即求出 \(k\) 的个数使得 \(a_i,a_{i+1},\cdots,a_k\) 根据上述贪心所分裂出来的数的最小值为 \(j\)（显然这个 \(j\) 也必须由 \(a_i\) 分裂零次或若干次得到），记为 \(f_{i,j}\)，那么答案加上 \(f_{i, j}\times \left(\left\lceil\dfrac{a_i}{j}\right\rceil - 1\right)\times i\)：因为至少要分裂 \(\left\lceil\dfrac{a_i}{j}\right\rceil-1\) 次才能让 \(a_i\leq j\)，而以 \(i\) 开头的每一个子段的左端点还可以被向左扩展 \(i\) 次。即若子段 \([i,k]\) 在 \(i\) 处至少分裂 \(j\) 次，则对于任何子序列 \([l,k](l\leq i\leq k)\)，\(a_i\) 分裂的次数都是 \(j\)，因为 \(a_i\) 的分裂不受前面的数的影响。这样的 \(l\) 共有 \(i\) 个，故需乘上 \(i\)（也就是说，我们在每个位置处统计该位置在所有子段中总分裂次数之和）。

看上去有 \(n ^ 2\) 个合法状态，但有些 \(j\) 是永远分裂不到的，例如若 \(a_i = 10\) 则 \(j = 9\) 无用，因为如果要使得分裂出来的数 \(\leq 9\)，则根据贪心思想我们会分成 \(5, 5\) 而不是 \(1, 9\)。类似的，\(j = 6, 7, 8\) 也无用。

实际上只有所有 \(j\in\left\{\left. \left\lfloor\dfrac{a_i}{d} \right\rfloor \right|\ d\in[1, a_i] \right\}\) 有用，这一点不难证明（注意，给定分裂得到的值计算 分裂次数 是上取整，但给定分裂次数计算 分裂得到的值 是下取整）。而根据数论分块的结论，有用的 \(j\) 只有 \(\sqrt {a_i}\) 个。

因此，我们可以直接枚举 \(l,r\) 表示用 \(a_i\) 整除 \(v \in [l, r]\) 上取整 后结果相同的一段区间，这个可以类似数论分块实现，详见 基础数论学习笔记 Part 5.2.1（数论分块是下取整后相同，而本题是上取整后相同）。则 \(f_{i, j}\) 可以由 \(\sum\limits_{k = l} ^ r f_{i + 1, k}\) 得到，其中 \(j = \left\lfloor\dfrac {a_i} {\left\lceil\frac {a_i} l \right\rceil} \right\rfloor\)。

上述转移式的来源：给定值 \(j\)，要求分裂出来的数均 \(\leq j\)，因为我们需要 使分裂次数最小，因此分裂次数是固定的 \(\left\lceil\dfrac {a_i} j \right\rceil\)。因此，使分裂次数相同的值即使 \(a_i\) 整除后上取整相同的一段值域区间 \([l, r]\)。同时，我们分裂得到的数的较小值即 \(\left\lfloor\dfrac {a_i} {\left\lceil\frac {a_i} l \right\rceil} \right\rfloor\)，因为分裂了 \(\left\lceil\dfrac {a_i} l \right\rceil\) 次。

用不定长数组 vector 来存储每一位的答案，时间复杂度 \(\mathcal{O}(n\sqrt {a_i})\)，空间复杂度 \(\mathcal{O}(n)\)。代码。

III. P2260 [清华集训2012]模积和

求 \(\sum\limits_{i = 1} ^ n n \bmod i\) 是经典问题：拆成 \(\sum\limits_{i = 1} ^ n \left(n - \left\lfloor\dfrac n i\right\rfloor\times i\right)\) 后数论分块，时间复杂度 \(\mathcal{O}(\sqrt n)\)。

原式可以写作

\[\left(\sum_{i = 1} ^ n n\bmod i\right) \left(\sum_{i = 1} ^ m m\bmod i\right) - \sum_{i = 1} ^ {\min(n, m)} \left(n - \left\lfloor\dfrac n i \right\rfloor i\right)\left(m - \left\lfloor\dfrac m i\right\rfloor i \right) \]

全部可以使用数论分块解决。可能需要的公式：\(\sum_{\\i=1}^ni^2=\dfrac{n(n+1)(2n+1)}6\)。时间复杂度 \(\mathcal{O}(\sqrt n)\)。

6. 阶与原根

原根，数论的王！

模 \(n(n > 1)\) 的简化剩余系在模 \(n\) 乘法意义下封闭且构成群。容易证明其满足封闭性和结合律，存在逆元和单位元。将群相关定义应用在其上，得到阶和原根（循环群的生成元）的概念。

6.1 阶

阶的定义如下：使得 \(a ^ x \equiv 1\pmod m\) 的最小的 正整数 \(x\) 被称为 \(a\) 模 \(m\) 的阶，记作 \(\delta_m(a)\)。

容易发现，\(a\perp m\) 是 \(\delta_m(a)\) 存在的 充要条件。必要性：若 \(a\) 与 \(m\) 不互质，显然 \(a ^ x\) 与 \(m\) 不互质，因此模 \(m\) 不可能得 \(1\)。充分性：若 \(a\perp m\)，根据欧拉定理，\(x = \varphi(m)\) 即一解，因此阶存在。

• 阶就是将一个数自乘若干次后模 \(m\)，第一次得到 \(1\) 的自乘次数。之所以是得到 \(1\)，因为 \(1\) 的性质很好。例如它和所有数互质，且 \(1\) 的任何次幂均为 \(1\)，且 \(1\) 是 \(1\) 在模任何正整数意义下的乘法逆元，因此我们可以在同余方程的任意位置除以已经被证明等于 \(1\) 的部分，而不需要担心不存在逆元。

接下来给出一些关于阶的性质。以下讨论均基于 \(a\perp m\)。

• 若 \(a ^ x\equiv 1\pmod m\)，则 \(a ^ {kx}\equiv 1\pmod p\)。因此所有使得 \(a ^ x\equiv 1\pmod p\) 的 \(x\) 必然是 \(x_{\min}\) 即 \(\delta_m(a)\) 的倍数。

性质 1：\(a ^ x \equiv 1\pmod m\) 当且仅当 \(\delta_m(a)\mid x\)。若非，则令 \(r = x\bmod \delta_m(a)\)，\(a ^ r\equiv 1\pmod m\)，与阶的最小性矛盾。

性质 2：\(\delta_m(a ^ k) = \dfrac {\delta_m(a)}{\gcd(\delta_m(a), k)} = \dfrac {\mathrm{lcm}(\delta_m(a), k)}{k}\)。OI wiki 的证明较为复杂，笔者给出一个感性理解。

• 对于第一部分，注意到 \((a ^ k) ^ x = a ^ {kx}\)，因此根据性质 1，\(\delta_m(a ^ k)\) 为最小的 \(x\) 使得 \(\delta_m(a) \mid kx\)，因此 \(x_{\min} = \dfrac {\delta_m(a)}{\gcd(\delta_m(a), k)}\)（我们知道，若给定 \(a, b\)，则使 \(a\mid bx\) 的最小的 \(x\) 为 \(\dfrac {a}{\gcd(a, b)}\)，这一点可以对 \(a\) 的每个质因子单独分析得到）。
• 对于第二部分，因为能够整除 \(k\) 的最小的 \(\delta_m(a)\) 的倍数为 \(\mathrm{lcm}(\delta_m(a), k)\)（根据最小公倍数的定义易得），所以使得 \(a ^ {kx} \equiv 1\pmod m\) 的最小的 \(kx\) 即 \(\mathrm{lcm}(\delta_m(a), k)\)，故 \(x_{\min} = \dfrac {\mathrm{lcm}(\delta_m(a), k)}{k}\)。
• 上述两部分也可以根据 \(ab = \gcd(a, b) \times \mathrm{lcm}(a, b)\) 互相推导。

回收前文（3.1 BSGS）：当 \(a\perp p\) 时，使得 \(a ^ x\equiv b\pmod p\) 的 \(x\) 若存在，则有循环节 \(\delta_p(a)\)。证明显然。因此，为求出 \(a ^ x\equiv b\pmod p\) 的通解，我们可以求出 \(x\) 的最小解 \(x_0\) 和次小解 \(x_1\)，则 \(x = x_0 + k(x_1 - x_0)\ (k\in \N)\)，因为 \(x_1 - x_0 = \delta_p(a)\)。

---

下面给出求解 \(\delta_m(a)\) 的若干方法，其中 \(m \perp a\)。

法一：直接使用 BSGS 求 \(a ^ x\equiv 1 \pmod m\) 的最小正整数解。时间复杂度 \(\sqrt m\)。

法二：根据阶的性质 1，对于 \(x = k\delta_m(a)\)，必然有 \(a ^ x \equiv 1\pmod m\)。因此考虑首先令 \(x = \varphi(m)\)，然后对于 \(\varphi(m)\) 的每个质因子 \(p\)，用 \(x\) 不断试除 \(p\) 直到 \(x\) 无法整除 \(p\) 或 \(a ^ {\frac x p} \not\equiv 1\pmod m\)。时间复杂度 \(\mathcal{O}(\sqrt m + \log ^ 2 m)\)，因为需要分解质因数和求解欧拉函数，用 Pollard-rho 可以优化至 \(m ^ {0.25}\)。若 \(m\) 不大，则可 \(\mathcal{O}(m)\) 线性筛预处理每个数的最小质因子，单次查询即可 \(\log ^ 2 m\)。

6.2 原根

原根的定义如下：对于 \(m\in \N_{+}\)，\(a\in \Z\) 且 \(a\perp m\)，若 \(\delta_{m}(a) = \varphi(m)\)，则称 \(a\) 为模 \(m\) 的原根。

注意，并不是所有数均有原根。存在原根的模 \(m\) 缩系同构于循环群，因为原根这一概念等价于循环群的生成元。

我们需要原根的原因是它可以 生成 模 \(m\) 的缩系，即它的若干次幂在模 \(m\) 意义下取遍了所有与 \(m\) 互质的数。这使得我们在考虑解与模数互质且模数存在原根的同余方程时可以用原根的若干次幂代替未知数。这一点在求解高次剩余时非常有用。

• 我们将在众多数论毒瘤题中体会到原根威力之强大：它可以将指数上的问题转化为更简单的一般问题。

根据原根的定义，为判定 \(a\) 是否是 \(m\) 的原根，只需检查 \(a\) 的所有 \(\varphi(m)\) 的 真因数 次幂模 \(m\) 是否均不等于 \(1\)。这等价于检查 \(\varphi(m)\) 除以其质因子是否是 \(a\) 的阶的倍数，因为 \(\varphi(m)\) 除以其某一质因子所得的所有数覆盖了 \(\varphi(m)\) 的所有真因数。因此，我们有

原根判定定理：对于 \(m\geq 3\)，\(a\perp m\)，\(a\) 是 \(m\) 的原根的 充要条件 是对于任意 \(\varphi(m)\) 的质因子 \(p\)，均有 \(a ^ {\frac {\varphi(m)} p} \not\equiv 1\pmod m\)。

证明：必要性显然。

充分性：因为 \(\dfrac {\varphi(m)} p\) 的所有因子取遍了 \(\varphi(m)\) 除了其本身的所有因子，所以若存在 \(a ^ d\equiv 1\pmod m\) 使得 \(d < \varphi(m)\)（容易证明 \(d\mid \varphi(m)\)），则必然存在 \(\varphi(m)\) 的质因子 \(p\) 使得 \(d \left|\dfrac{\varphi(m)}{p} \right.\)，这说明存在 \(a ^ {\frac {\varphi(m)} p} \equiv 1\pmod m\)，与假设矛盾。证毕。

除了判断一个数是否是原根，我们也需要判断一个数是否有原根。

原根存在定理：一个数 \(m\) 存在原根的 充要条件 是 \(m = 2, 4, p ^ \alpha, 2p ^ \alpha\)，其中 \(p\) 是 奇质数。

证明过于复杂，略去。读者可以当成重要结论记住。

---

以下是原根与阶相结合的一些知识。

若 \(m\) 存在原根，则使得 \(\delta_m(a) = l\) 的 \(a\) 的个数为 \(\begin{cases} 0 & l \nmid \varphi(m) \\ \varphi(l) & l \mid \varphi(m) \end{cases}\)。

根据阶的性质 1，第一部分显然。

考虑证明第二部分：设 \(g\) 为 \(m\) 的一个原根。因为对于任意 \(a\perp m\) 均可表示为 \(g ^ k(0\leq k < \varphi(m))\)，所以问题即求出使得 \(\delta_m(g ^ k) = l\) 的 \(k\) 的个数。根据阶的性质 2，\(\delta_m(g ^ k) = \dfrac {\delta_m(g)}{\gcd(\delta_m(g), k)}\)，因此 \(\dfrac {\varphi(m)}{\gcd(\varphi(m), k)} = l\)，即 \(\gcd(\varphi(m), k) = \dfrac {\varphi(m)}l\)。根据欧拉函数的性质 10，满足该式 \(k\in [0, \varphi(m) - 1]\) 的个数即 \(\varphi\left(\dfrac {\varphi(m)}{\frac{\varphi(m)} l}\right)\)，即 \(\varphi(l)\)。

• 形象地说，将 \(g ^ k \bmod m\to g ^ {k + 1}\bmod m\) 看成一个长度为 \(\varphi(m)\) 的环。我们尝试在环上每次走 \(k\) 步形成一个子环，则 \(g ^ k\) 的阶即形成的环长。我们知道，如果在一个长为 \(n\) 的环上每次走 \(k\) 步，则能够走到的位置模 \(\gcd(n, k)\) 相同，且模 \(\gcd(n, k)\) 相同的位置均能被遍历到（这是 OI 中的经典结论，见 0.7），即环长为 \(\dfrac n {\gcd(n, k)}\)。因此，为使 \(\dfrac{\varphi(m)}{\gcd(\varphi(m), k )} = l\)，即 \(\gcd(\varphi(m), k) = \dfrac {\varphi(m)}{l}\)，即环长和步长的 \(\gcd\) 等于形成的子环个数，也等于环长除以子环长。根据欧拉函数的性质 10，合法的 \(k\) 的个数即 \(\varphi(l)\)。

上述结论从侧面反映了欧拉函数的性质 7：\(\sum\limits_{d \mid n} \varphi(d) = n\)。\(\sum\limits_{l \mid \varphi(m)} \varphi(l) = \varphi(m)\)，即模 \(m\) 的阶等于 \(l\) 的数的个数之和（也即在模 \(m\) 意义下存在阶的数的个数）等于与 \(m\) 互质的数的个数，而与 \(m\) 互质是在模 \(m\) 意义下存在阶的充要条件。

通过上述推导我们得到推论（原根个数定理）：若正整数 \(m\) 存在原根，则其原根的个数为 \(\varphi(\varphi(m))\)。

求出一个数的所有原根：考虑求出一个数的任意一个原根 \(g\)，根据上述结论，\(g ^ k\bmod m(k \perp \varphi(m))\) 也是 \(m\) 的原根。在 1959 年，中国数学家王元证明了最小原根的级别为 \(\mathcal{O}(m ^ {0.25 + \epsilon})\)。结合原根存在定理和原根判定定理，我们得以在 \(\mathcal{O}(m)\) 预处理每个数的最小质因子后单次 \(\mathcal{O}(m ^ {0.25}\omega(m)\log m)\) 求出 \(m\) 的最小原根，从而求出 \(m\) 的所有原根。

• 笔者在上网查找资料时发现中国科学院院士王元于 2021 年 5 月 14 日去世，为此笔者深感痛心。可能这位前辈也没有想到，在六十多年后的今天，他的研究成果已经成为信息学竞赛中数论领域的重要一环。笔者在此对他表示崇高的敬意。

---

关于原根，还有一个有趣且重要的性质：

若 \(m\) 存在原根 \(g\)，设 \(n = \varphi(m)\)，则 \(m\) 的简化剩余系与 \(n\) 次单位根 同构。

这是因为对于任何一个 \(a \perp m\)，其均可以写成 \(g ^ k\) 的形式。而任何一个 \(n\) 次单位根 \(\omega_k\) 也可以写成 \(\omega_1 ^ k\) 的形式。同时，\(g ^ k \equiv 1\pmod p\)，且 \(\omega_1 ^ n = 1\)。因此，我们可以将单位圆应用在 \(m\) 的简化剩余系上，为原根提供了一个形象的表示方法，如下图。

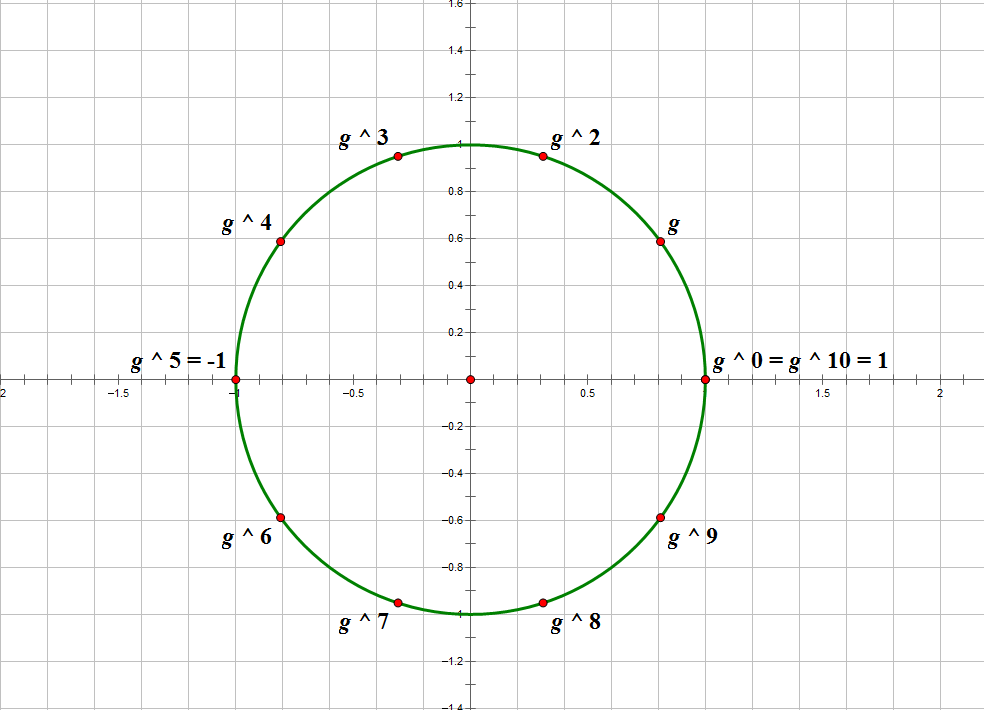
图中，单位根的 \(0\sim 9\) 次幂将单位圆若干等分。\(10\) 次单位根 \(\omega_i \times \omega_j = \omega_{(i + j)\bmod 10}\) 恰好对应着 \(g ^ i\times g ^ j \equiv g ^ {(i + j)\bmod 10}\pmod {11}\)，圆环上运算（两个数相乘）的循环往复（体现为逆时针旋转）体现了 模 这一操作。

这也是为什么对于特定模数，我们可以使用原根代替 \(n\) 次单位根进行快速傅里叶变换：\(\varphi(998244353) = 2 ^ {22}\times 238\)，所以当需要使用 \(2 ^ k\) 次单位根时，若 \(k\) 不超过 \(\varphi(p)\) 当中质因子 \(2\) 的个数且 \(p\) 存在原根，即可用原根代替 \(2 ^ k\) 次单位根。也就是快速数论变换 NTT。

6.3 相关应用

总结一下，我们提出阶的定义是为了引出原根（至少在笔者所接触过的所有题目中，没有遇到直接与阶相关的问题），而原根的用处在于生成模 \(m\) 的简化剩余系。不要小看这个性质！它在 \(m\) 是质数或质数的幂时非常好用，可以生成除了 \(0\) 以外的任何数，几乎是神一样的存在！

我们介绍了阶的相关性质及其求法，以及原根的判定定理，存在定理与个数定理。其中，原根存在定理和最小原根级别的证明较为复杂，故略去，学有余力的读者可自行查阅资料。

• 在特定模数下，原根用于替换复数单位根进行快速傅里叶变换，如常见 NTT 模数 \(998244353\)，\(1004535809\) 等等。
• 求解高次剩余时，一步重要的转化是 将未知数用原根的若干次幂代替。

6.4 例题 *I. P5605 小 A 与两位神仙

前置知识：Pollard-rho & Miller-Rabin。

注意到模数 \(p\) 是奇质数的幂，存在原根 \(g\)。

尝试将 \(x\) 和 \(y\) 表示成 \(g ^ X\) 和 \(g ^ Y\) 的形式，则根据欧拉定理，\(x ^ a \equiv y\pmod p\) 等价于方程 \(Xa\equiv Y\pmod {\varphi(p)}\)。

根据裴蜀定理，后者存在解的充要条件是 \(\gcd(X, \varphi(p)) \mid Y\)，这等价于 \(\gcd(X, \varphi(p)) \mid \gcd(Y, \varphi(p))\)。

根据阶的性质 \(\delta_p(g ^ k) = \dfrac {\delta_p(g)}{\gcd(\delta_p(g), k)}\)，我们发现 \(\delta_p(x) = \dfrac {\varphi(p)} {\gcd(\varphi(p), X)}\)（其实这很好理解，在长为 \(\varphi(p)\) 的环上每一步走 \(X\) 长度，则需要 \(\dfrac {\varphi(p)}{\gcd(\varphi(p), X)}\) 步才能回到原来的位置 ），因此该条件又等价于 \(\delta_p(y)\mid \delta_p(x)\)。

直接 \(\mathrm{polylog}\) 求阶即可，在最开始需要使用 Pollard-rho 分解 \(\varphi(p)\)，时间复杂度 \(\mathcal{O}(n\log ^ 2p + p ^ {0.25})\)。

通过本题，我们得到这样的结论：对于奇质数的幂 \(p\) 和 \(x, y\perp p\)，\(x ^ a\equiv y\pmod p\) 有解当且仅当 \(\delta_p(y)\mid \delta_p(x)\)。

• 根据阶的性质，对于 \(a = k\delta_p(x)\)，必然有 \(x ^ a \equiv 1\pmod p\)。因此考虑首先令 \(a = \varphi(p)\)，然后对于 \(\varphi(p)\) 的每个质因子 \(q\)，用 \(a\) 不断试除 \(q\) 直到 \(a\) 无法整除 \(q\) 或 \(x ^ {\frac a q} \not\equiv 1\pmod p\)​。

*II. P6730 [WC2020] 猜数游戏

和上面一题差不多的思路。

分成 \(a\) 与 \(p\) 互质和 \(a\) 与 \(p\) 不互质两种情况考虑。并且将每个数的贡献拆开来考虑，即求出有多少种情况使得 \(a\) 对答案有贡献。

当且仅当 \(S\) 中不存在一个数能生成 \(a\) 时，\(a\) 对答案有贡献。因此对每个 \(a\),答案加上 \(2 ^ {n - c}\)，其中 \(c\) 是能生成 \(a\) 的数的个数。

当 \(a\) 与 \(p\) 不互质时，因为 \(p\) 是奇质数的幂，所以在不超过 \(\log\) 次后 \(a\) 的幂变为 \(0\)，因此直接考虑每个数能生成哪些数即可得到每个数能被多少个数生成。使用哈希表存储，该部分时间复杂度 \(n\log p\)​。

当 \(a\) 与 \(p\) 互质时，直接使用上一题的结论，对每个数求阶后做高维后缀和即可。注意若两个数能互相生成，即阶相等，则需要钦定一个顺序，使得前面的数钦定生成后面的数。

7. 高次剩余问题

• Warning：本章难度较大。

若 \(b\) 在模 \(p\) 意义下能表示为某个数 \(x\) 的 \(a\) 次方，则称 \(b\) 为模 \(p\) 意义下的 \(a\) 次剩余。

\(a\) 次剩余问题即求解形如 \(x ^ a\equiv b\pmod p\) 的方程。注意未知量 \(x\) 在底数处，而非离散对数问题的指数处。

7.1 拉格朗日定理

我们知道代数学基本定理：任何 \(n\) 次多项式在复数域有且只有 \(n\) 个可重根。那么，在模意义下是否仍然满足多项式的 不同 的根的个数不超过多项式次数呢？

拉格朗日定理告诉我们如下事实：对于模 质数 \(p\) 意义下的整系数多项式 \(f(x) = \sum\limits_{i = 0} ^ n a_i x ^ i\)，其中 \(p\nmid a_n\)，则 \(f(x)\equiv 0\pmod p\) 在模 \(p\) 意义下 至多 有 \(n\) 个 不同 解。

证明：考虑数学归纳法。当 \(n = 0\) 时成立，因为 \(a_0 \equiv 0\pmod p\) 无解（注意 \(p\nmid a_0\)）。

当 \(n > 0\) 时，不妨设方程有 \(n + 1\) 个 不同 解 \(x_0, x_1, \cdots, x_n\)。因为 \(f(x_0) \equiv 0\pmod p\)，所以 \(f(x)\) 必然可以被因式分解为 \((x - x_0)g(x)\)，其中 \(g(x)\) 是一个不超过 \(n - 1\) 次的多项式。

因为 \(x_i \neq x_0(1\leq i \leq n)\) 且 \((x_i - x_0)g(x_i) \equiv 0\pmod p\)，故 \(x_1, x_2, \cdots, x_n\) 均为 \(g(x)\) 的根，与归纳假设矛盾。命题得证。

7.2 二次剩余 7.2.1 定义与符号

根据定义，若存在 \(x\) 使得 \(x ^ 2 \equiv a\pmod p\)，则称 \(a\) 为模 \(p\) 的 二次剩余，反之则称 \(a\) 为模 \(p\) 的 二次非剩余。注意，这两个定义均基于 \(a\) 不是 \(p\) 的倍数的基础上。也就是说，若 \(a\) 是 \(p\) 的倍数，则 \(a\) 既不是模 \(p\) 的二次剩余，也不是模 \(p\) 的二次非剩余。

勒让德符号：记作 \(\left(\dfrac a p\right)\)。当 \(a\) 是模 \(p\) 的二次剩余时，该值为 \(1\)；当 \(a\) 是模 \(p\) 的二次非剩余时，该值为 \(-1\)；当 \(a\) 是 \(p\) 的倍数时，该值为 \(0\)。

• 勒让德符号在二次互反律的表示中很有用，但是我们不讲二次互反律。
• 直观认知：能被表示成 \(g ^ {2k}\) 的数是二次剩余，反之则是二次非剩余。设 \(a = g ^ k\)，\(x = g ^ y\)，则 \(x ^ 2 = g ^ {2y}\)。要使 \(x ^ 2 \equiv a\pmod p\)，则 \(k\equiv 2y\pmod {p - 1}\)。因为 \(p - 1\) 是偶数，所以当 \(k\) 为奇数时，\(y\) 无解，反之则有两解（详见 1.4 节第三条），每一个 \(y\) 的解对应一个 \(x = g ^ y\)。

7.2.2 二次剩余的数量

以下讨论均基于 \(p\) 为奇质数。

根据拉格朗日定理，对于二次剩余 \(a\)，使得 \(x ^ 2 \equiv a\pmod p\) 成立的不同的 \(x\) 恰有两个。不妨设 \(x_0\) 为其中一解，显然 \(x_1 = -x_0\) 也为一解，且因 \(p\) 是奇质数所以 \(x_0\not\equiv x_1 \pmod p\)。这说明若 \(a\) 为模 \(p\) 的二次剩余，则存在两个不同且互为相反数的使 \(x ^ 2\equiv a \pmod p\) 成立的 \(x\)。

如果不用拉格朗日定理，我们也可以证明这一结论（思路来自 Kewth，详见参考资料）：设 \(x_0\) 和 \(x_1\) 是任意两个不同的使方程成立的解，则 \(x_0 ^ 2 \equiv x_1 ^ 2\pmod p\)，即 \((x_0 - x_1)(x_0 + x_1) \equiv 0\pmod p\)。所以 \(x_0 + x_1 \equiv 0\pmod p\)。这说明 \(x_0\) 和 \(x_1\) 互为相反数。我们知道，一个数的相反数只有一个，因此 \(x\) 至多且必然有两解（因为 \(a\) 是二次剩余）。

• 这和实数意义下的平方根几乎完全一样：正数（二次剩余）的平方根有两个且互为相反数，负数（二次非剩余）没有平方根。

因为 \(1\sim p - 1\) 当中任意一对相反数平方后均给出相同且独一无二的二次剩余，故模奇质数 \(p\) 意义下二次剩余的数量和二次非剩余的数量均为 \(\dfrac {p - 1}2\)。

• 感性认知：所有原根的偶数次幂和所有原根的奇数次幂将 \(1\sim p - 1\) 分成了两类，偶数类对应二次剩余，奇数类对应二次非剩余。

7.2.3 欧拉判别准则

• \(\dfrac {p - 1} 2\) 的偶数倍一定是 \(p - 1\) 的倍数，而 \(\dfrac {p - 1} 2\) 的奇数倍一定不是。\(g ^ {p - 1}\equiv 1\pmod p\)，而 \(g ^ {\frac {p - 1} 2}\equiv -1\pmod p\)。

利用欧拉判别准则，我们可以判断一个数 \(a\) 是否是 奇素数 \(p\) 的二次剩余。它给出如下定理：

\[a ^ {\frac{p - 1}2} = \left(\dfrac a p\right) \]

也就是说，当 \(a\) 是二次剩余时，\(a ^ {\frac {p - 1} 2} \equiv 1\pmod p\)。当 \(a\) 是二次非剩余时，\(a ^ {\frac {p - 1} 2} \equiv -1\pmod p\)。

证明（来自 Kewth）：\(a \mid p\) 时定理显然成立，考虑 \(a\nmid p\)。根据费马小定理，\(a ^ {p - 1} \equiv 1\pmod p\)。所以 \(a ^ {\frac {p - 1} 2}\) 只能等于 \(1\) 或 \(-1\)。因此欲证欧拉判别准则，只需证 \(a ^ {\frac {p - 1} 2} \equiv 1\pmod p\) 当且仅当 \(a\) 是二次剩余。

充分性：当 \(a\) 是二次剩余时，令 \(x ^ 2 \equiv a\pmod p\)。显然 \(x\perp p\)，因此 \(a ^ {\frac {p - 1} 2} = x ^ {p - 1} \equiv 1\pmod p\)。

必要性：因为 \(p\) 是奇素数，故存在原根 \(g\)。不妨设 \(a \equiv g ^ k\pmod p\)。根据原根的定义，\(g ^ {\frac {p - 1} 2} \not\equiv 1\pmod p\)，故 \(g ^ {\frac{p - 1} 2} \equiv -1\pmod p\)。因为 \((g ^ k) ^ {\frac {p - 1} 2} \equiv (-1) ^ k \equiv 1 \pmod p\)，所以 \(k\) 为偶数。因此 \(\left(g ^ {\frac k 2}\right) ^ 2 \equiv a \pmod p\)，即 \(a\) 为二次剩余。得证。

• 另一种理解方法：当 \(k\) 为奇数时，\((g ^ k) ^ {\frac {p - 1} 2} = \left(g ^ {\frac {p - 1}2}\right) ^ k \equiv (-1) ^ k = -1\pmod p\)。根据 6.2 节中提到的等价类与单位根的同构性，上述事实恰对应着 \(p - 1\) 次单位根 \(\omega_k\) 当 \(k\) 为偶数时 \(\omega_k ^ {\frac {p - 1} 2} = 1\)，当 \(k\) 为奇数时 \(\omega_k ^ {\frac {p - 1}2} = -1\)。

  简单地说，\(a\) 是否是二次剩余 等价于 \(a ^ {\frac {p - 1} 2}\) 是否等于 \(1\) 等价于 \(a\) 能否被表示成 \(p\) 的一个原根的 偶数 次幂。读者应当仔细体会其中的等价关系。

欧拉判别准则同时也告诉我们勒让德符号关于 \(a\) 是完全积性函数，即对于任意 \(a, b\)，均有 \(\left(\dfrac a p\right)\left(\dfrac b p\right) = \left(\dfrac {ab} p\right)\)。

接下来介绍一个求解二次剩余的常用算法。

7.2.4 Cipolla 算法

Cipolla 可以在 \(\rm polylog\) 时间内求解模 奇质数 意义下的二次剩余，即给定 \(a\)，求出使得 \(x ^ 2 \equiv a \pmod p\) 的所有 \(x\)（显然有根号时间复杂度求解二次剩余的算法：BSGS）。

根据 7.2.2 节的分析，我们只需求出任意一个 \(x\)，然后取相反数即可。

学习 Cipolla 算法，我们首先需要了解 模意义下扩域 的技巧。读者可以理解为从 “整数” 扩张到了 “整系数复数”。

设 \(\omega\) 为一个二次非剩余，\(i ^ 2 \equiv \omega\pmod p\)。这样的 \(i = \sqrt \omega\) 在模 \(p\) 意义下的整数域中不存在，但是我们可以人为规定它存在（类似规定虚数单位 \(i = \sqrt {-1}\) 存在）。因此我们得到了形如 \(a + bi\) 的数。笔者习惯将其称为模 \(p\) 意义下以 \(\sqrt w\) 为虚数单位的复数。

即定义数域 \(F = \{a + bi \mid a, b \in [0, p - 1] \cup \Z\}\)。容易证明该数域封闭（类比复数域封闭），如乘法运算法则即 \((a + bi)(c + di) = ((ac + bd\omega) \bmod p) + ((ad + bc) \bmod p)i\)，且满足我们常见代数结构的几乎所有代数性质，如乘法结合律，乘法分配律等。

这个技巧常见于 模意义下二次非剩余强制开方。例如，\(5\) 在模 \(10 ^ 9 + 7\) 意义下没有二次剩余，故在计算斐波那契数列时，需要将一个数表示为 \(a +b\sqrt 5\) 的形式。

• Warning：前方有魔法。

考虑找到一个正整数 \(b\) 使得 \(\omega \equiv b ^ 2 - a\) 为二次非剩余，令 \(i ^ 2 \equiv b ^ 2 - a\)，即 \(i = \sqrt \omega\)。我们断言 \((b + i) ^ {\frac {p + 1} 2}\) 为 \(a\) 的二次剩余。

证明 Cipolla 算法的正确性需要两个引理。

1. \(i ^ p \equiv -i\pmod p\)。由欧拉判别准则，\(i ^ {p - 1} \equiv \omega ^ {\frac {n - 1} 2} \equiv -1\pmod p\)。
2. \((x + y) ^ p \equiv x ^ p + y ^ p\pmod p\)。由二项式定理，\((x + y) ^ p = \sum\limits_{i = 0} ^ p\dbinom p i x ^ i y ^ {p - i}\)，因为当 \(1\leq i < p\) 时，\(\dbinom p i\) 的分子含有质因子 \(p\) 而分母不含，故 \(\dbinom p i\) 为 \(p\) 的倍数。因此我们只需保留 \(i = 0\) 和 \(i = p\) 的项，即 \(x ^ p + y ^ p\)（有读者可能会因为 \(x\) 是模意义下复数而产生疑问，设 \(x = c +di\)，则 \(xp = (cp) + (dp)i \equiv 0 + 0i \equiv 0\pmod p\)）。

\[\begin{aligned} & \left((b + i) ^ {\frac {p + 1} 2} \right) ^ 2 \\ = \ & (b + i) ^ {p + 1} \\ \equiv \ & (b + i) (b ^ p + i ^ p) \\ \equiv \ & (b + i) (b - i) & (b ^ {p - 1}\equiv 1\pmod p) \\ \equiv \ & b ^ 2 - i ^ 2 \\ \equiv \ & a \pmod p \end{aligned} \]

证毕。

接下来是一些需要处理的细节。

1. 可以证明当 \(b\) 随机时，\(b ^ 2 - a\) 的二次剩余性均匀随机（但是笔者查阅的所有资料均没有给出完整证明，故略去）。因此，我们期望随机两次就可以找到这样的 \(b\)。
2. 为证明 \((b + i) ^ {\frac {p - 1} 2}\) 的虚部为 \(0\)，只需证明不存在 \((c + di) ^ 2\equiv a\pmod p\)，其中 \(d\neq 0\)。假设存在，对比等式两侧虚部，必然有 \(2cdi \equiv 0\pmod p\)，因此 \(c\equiv 0\pmod p\)。带入，得 \(d ^ 2\omega = a\)。因为 \(d ^ 2\) 和 \(a\) 均为二次剩余，所以 \(\omega\) 必然为二次剩余（勒让德符号的完全积性），矛盾。证毕。

综上，Cipolla 算法的时间复杂度为 \(\mathcal{O}(\log p)\)。代码见例题部分 I.

7.2.5 任意模数二次非剩余

什么？怎么会有出题人毒瘤到考这种玩意？

7.2.6 总结

二次剩余相关知识繁多，抓住 原根可近似看做单位根 这一关键线索有助于更好地理解奇素数 \(p\) 的二次剩余个数为 \(\dfrac {p - 1} 2\) 这一事实与欧拉判别准则。

从另一种角度：\(a = g ^ k\) 当中 \(k\) 的奇偶性出发，结合 exgcd 的推论（当 \(a, p\) 不互质时方程 \(ax\equiv b\pmod p\) 的解的情况，详见 1.4 节）也可以推得这些定理。

关于欧拉判别准则，笔者的理解是，对于任意奇素数 \(p\) 均有 \(a ^ {p - 1}\equiv 1\pmod p\)。给指数除以 \(2\) 相当于为左式开根。因此，\(1\sim p - 1\) 当中的所有数会因为自身性质的不同而 分化 成两类，一类是二次剩余，满足 \(a ^ {\frac {p - 1} 2} \equiv 1\pmod p\)，另一类是二次非剩余，满足 \(a ^ {\frac {p - 1} 2} = -1\pmod p\)。这种分化，用单位根的知识来解释，即对于 \(p - 1\) 次单位根 \(\omega_k\)，当 \(k\) 为偶数时 \(\omega_k ^ {\frac {p - 1} 2} = 1\)，反之则为 \(-1\)。而原根和单位根的联系

\[g ^ k \Leftrightarrow (\omega_1) ^ k \Leftrightarrow \omega_k \]

恰好解释了 \(a = g ^ k\)，\(k\) 的奇偶性对 \(a\) 是否是二次剩余的影响。

因此，笔者认为理解二次剩余的核心在于体会到 原根和单位根的等价性，以及 原根指数的奇偶性起到的关键影响。这对于理解更高次剩余也有极大帮助。是时候再贴出这张图了。

Cipolla 算法的巧妙构造令人惊叹，可惜的是，

“如果读者或听众不能够理解在人类力所能及的范围怎样可能找到这样一个论证，如果他不能从推导过程中得出任何关于他自己怎样能找到这样一个论证的建议，那么这个推导就可能是难以接受的，而且没有指导意义。”

所以读者只需记住这样的构造：找到 \(b\) 使得 \(b ^ 2 - a\) 是二次非剩余，令 \(i = \sqrt {b ^ 2 - a}\)，则 \((b + i) ^ {\frac{p + 1} 2}\) 即为所求。需要在模意义下扩域。

扩展：注意到当指数为 \(2\) 时，\(a ^ {\frac {p - 1} 2}\) 将 \(1\sim p - 1\) 分成两类。那么，当 \(d \mid p - 1\) 时，是否有 \(a ^ {\frac {p - 1} d}\) 的取值将 \(1\sim p - 1\) 分成 \(d\) 类？实际上是有的，读者可结合 \(p - 1\) 次单位根的性质和 \(k\) 模 \(d\) 的余数尝试推导结论。

\[(g ^ k) ^ {\frac {p - 1} d} = \left(g ^ \frac{p - 1} d\right) ^ k = \left(g ^ \frac{p - 1} d\right) ^ {\lfloor \frac {k} d \rfloor d} \left(g ^ \frac{p - 1} d\right) ^ {k\bmod d} \equiv \left(g ^ \frac{p - 1} d\right) ^ {k \bmod d}\pmod p \]

7.3 高次剩余

咕咕咕。

7.4 例题 I. P5491 【模板】二次剩余

#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
int T, n, p, b, w;
struct comp {
	int a, b;
	comp operator + (comp c) {return {(a + c.a) % p, (b + c.b) % p};}
	comp operator * (comp c) {return {(1ll * a * c.a + 1ll * b * c.b % p * w) % p, (1ll * a * c.b + 1ll * b * c.a) % p};}
};
int ksm(int a, int b) {int s = 1; while(b) {if(b & 1) s = 1ll * s * a % p; a = 1ll * a * a % p, b >>= 1;} return s;}
comp ksm(comp a, int b) {comp s = {1, 0}; while(b) {if(b & 1) s = s * a; a = a * a, b >>= 1;} return s;}
void solve() {
	cin >> n >> p;
	if(!n) return puts("0"), void();
	if(ksm(n, p - 1 >> 1) == p - 1) return puts("Hola!"), void();
	do b = rnd() % p; while(ksm(w = (1ll * b * b - n + p) % p, p - 1 >> 1) != p - 1);
	int x = ksm((comp){b, 1}, p + 1 >> 1).a;
	cout << min(x, p - x) << " " << max(x, p - x) << "\n";
}
int main(
	cin >> T;
	while(T--) solve();
	return 0;
}

*II. P6610 [Code+#7]同余方程

究极神仙题。

根据 \(\mu(p) \neq 0\) 不难想到使用 CRT 将问题拆分为模奇质数。每个奇质数的解的个数的积即为所求，因为从每个奇质数的解中任选一个，根据中国剩余定理，所有奇质数对应的解组合起来唯一确定一个解。

拆成奇质数是为了使二次剩余相关定理适用。接下来 \(p\) 均视为奇质数。

问题转化为求解 \(x\) 能被拆分成多少组 \(a, b\) 的和，使得 \(a, b\) 均为二次剩余或 \(0\)。其中，每个二次剩余的贡献系数是 \(2\)（一个二次剩余可被表示两个数的平方），\(0\) 的贡献是 \(1\)，每组 \((a, b)\) 的贡献即 \(a\) 和 \(b\) 分别的贡献系数之积。

我们需要一个数学公式而非判断式来描述答案，因为判断式是不可化简的。

二次剩余对应 \(2\)，\(0\) 对应 \(1\)，二次非剩余对应 \(0\)，这使得我们想到勒让德符号：注意到 \(\left(\dfrac a p\right) + 1\) 等价于使得 \(x ^ 2 \equiv a \pmod p\) 的 \(x\) 的个数，因此答案为

\[\sum\limits_{a + b \equiv x} \left(\left(\dfrac a p\right) + 1\right)\left(\left(\dfrac b p\right) + 1\right) \]

\(p\) 以内的二次剩余和二次非剩余个数相等，故 \(\sum\limits_{i = 0} ^ {p - 1} \left(\dfrac i p\right) = 0\)。再根据 \(b \equiv x - a\) 和勒让德符号的完全积性，上式简化为

\[p + \sum\limits_{a = 0} ^ {p - 1} \left(\dfrac {ax - a ^ 2} p\right) \]

接下来是一步巧妙转化。考虑到为 \(ax - a ^ 2\) 除以 \(a ^ 2\) 并不影响它的二次剩余性，因此答案即

\[p + \sum\limits_{a = 1} ^ {p - 1}\left(\dfrac {\frac x a - 1} p\right) \]

显然，对于 \(x \neq 0\) 且 \(a \in [1, p - 1]\)，\(\dfrac x a\) 取遍 \([1, p - 1]\)，即 \(\dfrac x a - 1\) 取遍 \([0, p - 2]\)。故当 \(x \neq 0\) 时，答案又可写为

\[p - \left(\dfrac {-1}{p}\right) \]

根据欧拉判别准则公式 \(\left(\dfrac a p\right) \equiv a ^ {\frac {p - 1} 2} \pmod p\) 上式即 \(p - (-1) ^ {\frac {p - 1} 2}\)。

对于 \(x = 0\)，答案 \(p + \sum\limits_{a = 1} ^ {p - 1} \left(\dfrac {-1} p\right)\) 即 \(p + (p - 1)(-1) ^ {\frac {p - 1} 2}\)。

公式已经足够简洁，可以 \(\mathcal{O}(1)\) 计算。时间复杂度 \(\mathcal{O}(p + n\omega(p))\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 5;
int T, p, x, cnt, ans = 1, pr[N], mnpr[N];
bool vis[N];
int calc(int x, int p) {return !x ? p % 4 == 1 ? 2 * p - 1 : 1 : p - (p % 4 == 1 ? 1 : -1);}
int main() {
	for(int i = 2; i < N; i++) {
		if(!vis[i]) mnpr[i] = pr[++cnt] = i;
		for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
			vis[i * pr[j]] = 1, mnpr[i * pr[j]] = pr[j];
			if(i % pr[j] == 0) break;
		}
	}
	cin >> T;
	while(T--) {
		cin >> p >> x, ans = 1;
		while(p != 1) ans *= calc(x % mnpr[p], mnpr[p]), p /= mnpr[p];
		cout << ans << "\n";
	}
	return 0;
}

8. 卢卡斯定理

前置知识：组合数，二项式定理。

卢卡斯定理是连接组合数学和数论的重要桥梁。

• Note：相比 Lucas，exLucas 的推导过程更加自然。

8.1 定理介绍

根据 0.6 节的结论，当 \(p\) 是质数时，\(\dbinom n m \bmod p = 0\) 当且仅当 \(n\) 减去 \(m\) 在 \(p\) 进制下需要借位，这等价于 \(n\) 在 \(p\) 进制下的每一位均不小于 \(m\)。

我们知道，当 \(i < j\) 时，\(\dbinom i j\) 定义为 \(0\)。这启发我们思考，如果将 \(n, m\) 表示为 \(p\) 进制数 \(n = \sum\limits_{i = 0} ^ c a_i p ^ i\) 和 \(m = \sum\limits_{i = 0} ^ c b_i p ^ i\)（不足的位均补 \(0\)，即 \(c = \max(\lfloor \log_p n \rfloor, \lfloor \log_p m\rfloor)\)），那么是否有 \(\dbinom n m\equiv \prod\limits_{i = 0} ^ c \dbinom {a_i}{b_i}\pmod p\)？

首先给出引理：当 \(p\) 是质数时，

\[(x + y) ^ p \equiv x ^ p + y ^ p\pmod p \]

是不是感觉非常眼熟？没错，在证明 Cipolla 算法的正确性时我们也使用了该引理。

证明：使用二项式定理将上式拆开，当 \(1\leq i < p\) 时 \(\dbinom p i\) 是 \(p\) 的倍数。证毕。

推论：\((1 + x) ^ p \equiv 1 + x ^ p\pmod p\)。

卢卡斯定理有两种等价的表示方法，一是

\[\dbinom{n}{m} \bmod p = \dbinom{\lfloor \frac n p \rfloor}{\lfloor \frac m p \rfloor}\dbinom{n\bmod p}{m\bmod p}\bmod p \]

二是

\[\dbinom n m \bmod p = \left(\prod \dbinom{a_i}{b_i}\right) \bmod p \]

其中 \(a_i, b_i\) 分别是 \(n, m\) 在 \(p\) 进制下的表示，即 \(n = \sum a_i p ^ i\)，\(m = \sum b_i p ^ i\)，且 \(p\) 为质数。

容易证明两种形式等价，因此我们只需证明第一种形式。

证明：设 \(n = dp + r(0\leq r < p)\)，即设 \(d = \left\lfloor \dfrac n p \right\rfloor\)，\(r = n\bmod p\)，则

\[\begin{aligned} & (1 + x) ^ n\\ = \ & (1 + x) ^ {dp} (1 + x) ^ {r} \\ \equiv \ & (1 + x ^ p) ^ {d} (1 + x) ^ {r} \pmod p \end{aligned} \]

上式 \(x ^ m\) 前的系数即 \(\dbinom n m\)。

因为 \((1 + x ^ p) ^ d\) 展开后 \(x\) 的次数均为 \(p\) 的倍数，\((1 + x) ^ r\) 展开后 \(x\) 的次数小于 \(p(r < p)\)，因此 \(x ^ m\) 项只能由 \((1 + x ^ p) ^ d\) 展开后的 \(x ^ {p\times \lfloor \frac m p \rfloor}\) 项与 \((1 + x) ^ r\) 展开后的 \(x ^ {m\bmod p}\) 项相乘得到。根据二项式定理，命题得证。

根据形式 1, 递归实现 Lucas 即可。\(\mathcal{O}(p)\) 预处理阶乘及其逆元 \(\mathcal{O}(1)\) 求组合数，单次 Lucas 的时间复杂度为 \(\mathcal{O}(\log_p n)\)。代码见例题部分 I.

卢卡斯定理告诉我们，当计算一个大组合数对 \(p\) 取模后的值时，可以将 \(n, m\) 在 \(p\) 进制下的每一位分开考虑，再将所得结果相乘。

特别地，若 \(n\) 在 \(p\) 进制下至少有一位小于 \(m\)，则 \(\dbinom n m \bmod p = 0\)，这是因为对于 \(a_i < b_i\)，\(\dbinom {a_i} {b_i} = 0\)。这符合我们一开始的猜想。

利用卢卡斯定理，我们可以快速计算组合数的奇偶性。为使 \(m\) 在二进制下每一位均不大于 \(n\)，必然有 \(n\ \&\ m = m\)。因此，\(\dbinom n m\) 是奇数当且仅当 \(n\) 和 \(m\) 的按位与等于 \(m\)，或者 \(n\) 和 \(m\) 的按位或等于 \(n\)。

8.2 扩展卢卡斯定理

当模数不是质数的时候，我们也有快速计算 \(\dbinom n m\bmod p\) 的方法。

首先，处理模数 \(p\) 为合数的情况，一般的思路是首先将 \(p\) 分解质因数为 \(\prod q_i ^ {k_i}\)，对模每个质数幂的情况单独求解，再 crt 合并。这就是 crt 的强大威力！

考虑计算 \(\dbinom n m \bmod {q ^ k}\)。自然是将组合数拆成 \(\dfrac {n !} {m!(n - m)!}\) 的形式。因为 \(m!(n - m)!\) 含有质因子 \(q\)，所以我们无法直接求解逆元。既然 \(q\) 这么麻烦，那就除掉好了。

考虑将组合数的分子和分母的所有质因子 \(q\) 全部除掉，即变形为

\[\dfrac {\frac {n!}{q ^ {v_q(n!)}}}{\frac {m!}{q ^ {v_q(m!)}}\frac{(n - m)!}{q ^ {v_q((n - m)!)}}} \times q ^ {v_q(n!) - v_q(m!) - v_q((n - m)!)} \]

看起来很吓人，但实际上我们只是做了一个简单变形。根据 0.5 节的结论，\(v_q(n!)\) 容易求得（为了求出后面那个 \(q\) 的幂次）。

此时分子和分母均不含因子 \(q\)，那么分别算出分子和分母，再对分母求逆元即可。问题转化为求 \(\dfrac {n!}{q ^ {v_q(n!)}}\)。

设 \(d = \left\lfloor\dfrac n q\right\rfloor\)，\(d_k = \left\lfloor\dfrac n {q ^ k}\right\rfloor\)，\(r = n\bmod {q ^ k}\)。既然除掉了所有质因子 \(q\)，自然想到将所有数分成 \(q\) 的倍数和非 \(q\) 的倍数讨论。

对于 \(q\) 的倍数，有 \(q, 2q, \cdots, dq\)，我们给每个数除掉一个 \(q\)，惊讶地发现问题变成了求 \(\dfrac{d!}{q ^ {v_q(d!)}}\)。这是一个递归形式的子问题，可以递归求解。当 \(d = 0\) 时达到递归边界。

对于非 \(q\) 的倍数，它们在模 \(q ^ k\) 意义下形成循环节

\[1, 2, \cdots, q - 1, q + 1, \cdots, 2q - 1, 2q + 1, \cdots, q ^ 2 - 1, q ^ 2 + 1, \cdots, q ^ k - 1 \]

因此我们只需计算 \((q ^ k!)_q ^ {d_k} \times (r!)_q \bmod {q ^ k}\)（关于记号，详见 0.4 威尔逊定理推论部分）。预处理 \(q ^ k\) 以内所有与 \(q\) 互质的数的积的前缀和，该部分可以 \(\mathcal{O}(1)\) 计算。

• Note：根据威尔逊定理的推论（详见 0.4 节），\((q ^ k!)_q\bmod {q ^ k}\) 等于 \(1\) 或 \(-1\)。因此第一项不需要快速幂，可以直接根据 \(d_k\) 快速计算。

综合上述讨论，我们得到

\[\dfrac {n!}{q ^ {v_q(n!)}} \equiv \dfrac{d!}{q ^ {v_q(d!)}} \times (q ^ k!)_q ^ {d_k} \times (r!)_q\pmod {p ^ k} \]

当 \(n < q\) 时，直接计算返回预处理结果（因为此时 \(\dfrac {n!}{q ^ {v_q(n!)}}\) 等于 \((n!)_q\)），否则使用递归式计算即可。单次时间复杂度 \(\mathcal{O}(\log_q n)\)。

• Note：递归下去的子问题是除以 \(q\)，而循环节个数是除以 \(q ^ k\)，一定要注意区分！笔者因为递归下去的子问题直接除以 \(q ^ k\) 调了一个小时。
• Note：注意区分 \(\dfrac {n!}{q ^ {v_q(n!)}}\) 和 \((n!)_q\)。前者仅将所有质因子 \(p\) 去掉，而后者将所有含有质因子 \(p\) 的数去掉了。

综上，我们得以在 \(\omega(p)\log n + \sum {q_i} ^ {k_i}\) 的时间内求出一个大组合数模任意数 \(p\) 的值。若模数固定且使用 \(\sum q_i ^ {k_i}\) 的时间预处理，则可以做到单次 \(\mathcal{O}(\omega(p)\log n)\)。代码见例题 III.

8.3 例题 I. P3807 【模板】卢卡斯定理

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int T, n, m, p, fc[N], ifc[N];
int ksm(int a, int b) {int s = 1; while(b) {if(b & 1) s = 1ll * s * a % p; a = 1ll * a * a % p, b >>= 1;} return s;}
int binom(int n, int m) {return 1ll * fc[n] * ifc[m] % p * ifc[n - m] % p;}
int lucas(int n, int m) {
	if(n % p < m % p) return 0;
	if(n < p) return binom(n, m);
	return 1ll * lucas(n / p, m / p) * binom(n % p, m % p) % p;
}
void solve() {
	cin >> n >> m >> p;
	for(int i = fc[0] = 1; i < p; i++) fc[i] = 1ll * fc[i - 1] * i % p;
	ifc[p - 1] = ksm(fc[p - 1], p - 2);
	for(int i = p - 2; ~i; i--) ifc[i] = 1ll * ifc[i + 1] * (i + 1) % p;
	cout << lucas(n + m, n) << endl;
}
int main() {
	cin >> T;
	while(T--) solve();
	return 0;
}

*II. [BZOJ2445]最大团

定义一张 \(n\) 个点的图是 “好图” 当且仅当它能被分成若干大小相等的完全图。节点有标号。记 \(n\) 个点的好图个数为 \(G(n)\)。求 \(m ^ {G(n)}\bmod 999999599\)。\(n, m\leq 2\times 10 ^ 9\)。

由于模数是质数，根据欧拉定理转化为求 \(G(n)\bmod (10 ^ 9 - 402)\)。

被分成的完全图大小 \(d\) 一定是 \(n\) 的约数，考虑枚举 \(d\mid n\) 并计算完全图大小为 \(d\) 时的方案数。

根据组合意义，从 \(n\) 个节点中选出 \(d\) 个点连成完全图，再从剩下 \(n - d\) 个节点中选出 \(d\) 个点连成完全图，以此类推。最后剩下的 \(d\) 个节点连成完全图。由于完全图之间无序，而我们枚举完全图的过程有序，因此还需要除以 \(\dfrac n d\) 的阶乘。记 \(c = \dfrac n d\)，则

\[\begin{aligned} ans & = \dfrac 1 {c!} \dbinom{n} {d, d, \cdots, d} \\ & = \dfrac {n!} {(d!) ^ c \times c!} \end{aligned} \]

我们没有简单的办法在优于线性的复杂度内快速计算一个数的阶乘，而且模数也不是质数。

观察 \(99999598\)，将其分解质因数后得到 \(2\times 13\times 5281\times 7283\)。这说明模数是 square-free number。考虑分别求上式对这四个质数取模后的结果，最后 crt 合并。

问题转化为计算 \(ans\) 对质数 \(p\) 取模后的结果，其中 \(p\) 均较小。

对于给定的 \(n\)，容易算出 \(n!\) 总共含有多少个质因子 \(p\)，即 \(\sum_{\\i \in \N^+} \dfrac n {p ^ i}\)。因此，先求出 \(ans\) 含有多少个质因子 \(p\)，若个数 \(>0\) 则直接返回 \(0\)。否则问题转化为计算一个数 \(v\) 的阶乘去掉所有质因子 \(p\) 后模 \(p\) 的结果，记为 \(\mathrm{cal}(v,p)\)。

接下来使用扩展卢卡斯定理的思想。

记 \(d=\left\lfloor\dfrac v p\right\rfloor\) 以及 \(r=v\bmod p\)。我们求出 除去 \(p\) 的倍数 后 \(v!\) 对 \(p\) 取模的值，再乘上 \(\mathrm{cal}(d, p)\)。因为 \(p, 2p, \cdots dp\) 这些被忽略的数除以 \(p\) 后变成了子问题 \(\mathrm{cal}(d, p)\)。

因此我们只需求出 \(\prod\limits_{i \in[1, v] \land i \nmid p} i\)。将所有 \(i\) 对 \(p\) 取模，即 \(((p - 1)!) ^ d r!\)。根据威尔逊定理，上式即 \((-1) ^ dr!\)，可以 \(\mathcal{O}(p)\) 预处理 \(\mathcal{O}(1)\) 计算。因为最多递归 \(\log_p v\) 次（每次将 \(v\) 除以 \(p\)），因此该部分复杂度 \(\mathcal{O}(\log v)\)。

综上，总时间复杂度 \(\mathcal{O}(d(n)\log n)\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5;
const int mod = 1e9 - 401;
const int P[4] = {2, 13, 5281, 7283};
int ksm(int a, int b, int p) {
	int s = 1;
	while(b) {
		if(b & 1) s = 1ll * s * a % p;
		a = 1ll * a * a % p, b >>= 1;
	}
	return s;
}
int T, n, m, ans, p, fc[N];
vector <int> factor;
int num(int n) {int s = 0; while(n) s += n /= p; return s;}
int wilson(int n) {
	if(n < p) return fc[n];
	int d = n / p, r = n % p;
	int res = 1ll * wilson(d) * fc[r] % p;
	return d & 1 ? p - res : res;
}
int calc(int d) {
	if(num(n) > num(n / d) + num(d) * (n / d)) return 0;
	return 1ll * wilson(n) * ksm(1ll * wilson(n / d) * ksm(wilson(d), n / d, p) % p, p - 2, p) % p;
}
int query() {
	for(int i = fc[0] = 1; i < p; i++) fc[i] = 1ll * fc[i - 1] * i % p;
	int res = 0;
	for(int d : factor) res = (res + calc(d)) % p;
	return res; 
}
int main() {
	cin >> T;
	while(T--) {
		cin >> n >> m, m %= mod, ans = 0;
		factor.clear(); // add this line =.=
		for(int i = 1; i * i <= n; i++)
			if(n % i == 0) {
				factor.push_back(i);
				if(i * i != n) factor.push_back(n / i);
			}
		int cur = 1;
		for(int i = 0; i < 4; i++) {
			int res = (p = P[i], query());
			int k = 1ll * (res - ans % P[i] + P[i]) * ksm(cur, P[i] - 2, P[i]) % P[i];
			ans += k * cur, cur *= P[i], ans %= cur; // excrt
		}
		cout << ksm(m, ans, mod) << endl;
	}
	return 0;
}

III. P4720 【模板】扩展卢卡斯定理/exLucas

#include <bits/stdc++.h>
using namespace std;
void exgcd(int a, int b, int &x, int &y) {
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int inv(int x, int p) {return exgcd(x, p, x, *new int), (x % p + p) % p;}
long long n, m;
int p, tp, ans, curp = 1, q, qk, fc[1000005];
long long num(long long n) {long long s = 0; while(n) s += n /= q; return s;}
int calc(long long n) {return n ? 1ll * calc(n / q) * (tp && n / qk & 1 ? qk - 1 : 1) % qk * fc[n % qk] % qk : 1;} // 注意 n / q 和 n / qk!
int solve() {
	tp = (qk & 1) || qk <= 4;
	for(int i = fc[0] = 1; i < qk; i++) fc[i] = 1ll * fc[i - 1] * (i % q ? i : 1) % qk;
	int pw = num(n) - num(m) - num(n - m), res = 1ll * calc(n) * inv(1ll * calc(m) * calc(n - m) % qk, qk) % qk;
	while(pw--) res = 1ll * res * q % qk; // 根据 0.6 的结论, 质因子在组合数中的个数为对数级别
	return res;
}
int main() {
	cin >> n >> m >> p;
	for(int i = 2; i <= p; i++) {
		if(i * i > p) i = p;
		if(p % i == 0) {
			q = i, qk = 1;
			while(p % i == 0) qk *= i, p /= i;
			ans += 1ll * (solve() - ans % qk + qk) * inv(curp, qk) % qk * curp, ans %= (curp *= qk); // excrt 直接合并更方便 
		}
	}
	cout << ans << endl; 
	return 0;
}

9. 结语

数论是信息学竞赛的一个广阔分支。尽管近年来重大考试中涉及数论的题目日渐稀少，但熟练掌握数论相关的各种算法及其推导过程，对我们的思维水平有极大锻炼。

因为数论，我们得以求解各种各样的同余方程（\(ax\equiv b\)，\(a ^ x\equiv b\)，\(x ^ a\equiv b\)）；得以利用各种各样的数论函数和反演公式推式子；得以在模数不是质数时将模数转化为质数的幂，为使用原根这一杀手锏提供条件；得以快速计算大组合数取模；我们甚至能够在亚线性时间内计算积性函数前缀和，这无疑是令人惊叹的。希望读者在阅读的过程中能够深刻体会到数论之美。

挖坑待填：

• 任意模数非二次剩余。
• n 次剩余。
• 莫比乌斯反演与狄利克雷卷积的博客的重构。
• 各种各样的筛法，如杜教筛，Min_25 筛。
• 类欧几里得算法。

10. 参考资料

• ycx，数论基础学习笔记。
• OI wiki，数论部分。
• Kewth，二次剩余题解。

【本文来源：武汉seo公司 http://www.5h5q.com复制请保留原URL】