论文解读（GIN）《How Powerful are Graph Neural Networks》

Title：《How Powerful are Graph Neural Networks?》
Authors：Keyulu Xu, Weihua Hu, J. Leskovec, S. Jegelka
Sources：2019, ICLR
Paper：Download
Code：Download
Others：2421 Citations, 45 References

　　GNN 目前主流的做法是递归迭代聚合一阶邻域表征来更新节点表征，如 GCN 和 GraphSAGE，但这些方法大多是经验主义，缺乏理论去理解 GNN 到底做了什么，还有什么改进空间。

　　GNN 的变体均是遵循两个步骤：邻居聚合（neighborhood aggregation） 和 图池化（graph-level pooling）。　　

　　GNN 广泛遵循递归邻域聚合（或消息传递）方案，其中每个节点聚合其邻居的特征向量来计算其新的特征向量。经过 $k$ 次聚合迭代后，一个节点由其转换后的特征向量表示，该特征向量捕获该节点的 $k$ 跳邻域内的结构信息。然后，可以通过池化来获得整个图的表示，例如，通过将图中所有节点的表示向量相加。

　　目前研究现状：新 GNN 的设计大多基于经验直觉、启发式和实验试验模式。目前对 GNN 的性质和局限性的理论理解很少，对 GNN 的表征能力的形式化分析也有限。

　　本文框架受 GNNs 和 WL 图同质测试，（Weisfeiler-Lehman (WL) graph isomorphism test ）[ Weisfeiler & Lehman, 1968]  的启发。与 GNNs 类似，WL test 通过聚合其网络邻居的特征向量来迭代更新给定节点的特征向量。使 WL test 如此强大的是它的内射聚合更新，它将不同的节点邻域映射到不同的特征向量。我们的关键见解是，如果GNN的聚合方案具有很高的表达性，并且可以建模内射函数，那么 GNN 就可以具有与 WL test 一样大的鉴别能力。

　　本文贡献：

• • 证明了GNN最多只和 Weisfeiler-Lehman (WL) test 一样有效，即 WL test 是GNN性能的上限；
  • 建立了邻域聚合（neighbor aggregation）和图读出函数（graph readout functions）的条件，在这些条件下，得到的 GNN 与 WL test 一样强大；
  • 识别了无法被流行的 GNN 变体区分的图结构，如 GCN 和 GraphSAGE ，并且精确地描述了基于 GNN 的模型可以捕获的图结构类型；
  • 开发了一个简单的神经结构，图同构网络(Graph Isomorphism Network——GIN)，并证明了它的判别、表征能力等于 WL test 的能力；

　　GNN 常见的两步走：1、聚合邻居信息；2、更新节点学习

　　GNN 的 第 $k$ 层 表达式：

　　　　$a_{v}^{(k)}=\text { AGGREGATE }^{(k)}\left(\left\{h_{u}^{(k-1)}: u \in \mathcal{N}(v)\right\}\right)$

　　　　$h_{v}^{(k)}=\operatorname{COMBINE}^{(k)}\left(h_{v}^{(k-1)}, a_{v}^{(k)}\right)$

　　AGGREGATE 比较典型的例子是 GraphSAGE：

　　GraphSAGE 的 AGGREGATE 被定义为：

　　　　$a_{v}^{(k)}=\operatorname{MAX}\left(\left\{\operatorname{ReLU}\left(W \cdot h_{u}^{(k-1)}\right), \forall u \in \mathcal{N}(v)\right\}\right)$

 　　这里的 $MAX $ 代表的是 element-wise max-pooling 。

 　　GraphSAGE 的 COMBINE 为 ：

　　　　$W \cdot\left[h_{v}^{(k-1)}, a_{v}^{(k)}\right]$

 　　而在 GCN(Kipf & Welling, 2017) 中，AGGREGATE 和 COMBINE 集成为：

　　　　$h_{v}^{(k)}=\operatorname{ReLU}\left(W \cdot \operatorname{MEAN}\left\{h_{u}^{(k-1)}, \forall u \in \mathcal{N}(v) \cup\{v\}\right\}\right)$

　　对于 node classification 任务，node representation $h_{v}^{(K)}$ 将作为预测的输入；对于 graph classification 任务，READOUT 函数聚合了最后一次迭代输出的节点表示$h_{v}^{(K)}$ ，并生成 graph's representation $h_{G}$ :

　　　　$ h_{G}=\operatorname{READOUT}\left(\left\{h_{v}^{(K)} \mid v \in G\right\}\right)$

　　其中：READOUT 可以是简单的 permutation invariant function，比如：summation，或者是更加复杂的 graph-level pooling function 。

　　图同构问题（ graph isomorphism problem）：询问这两个图在拓扑结构上是否相同。

　　WL test  为了辨别多标签图，具体步骤如下：[ 参考《Weisfeiler-Lehman(WL) 算法和WL Test》 ]

• • 迭代地聚合节点及其邻域的标签；
  • 将聚合后的标签散列为唯一的新标签。如果在某次迭代中，两个图之间的节点标签不同，则该算法判定两个图是非同构的；

　　基于 WL test 的多图相似性判别算法 WL subtree kernel 也被提出，图示如下：

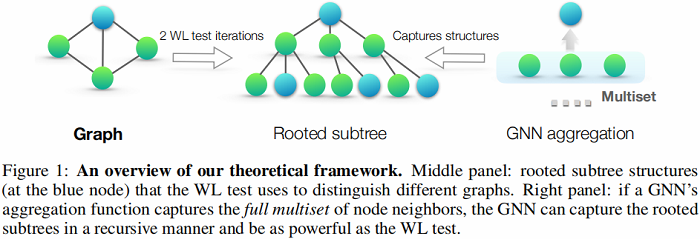
　　图示分析：如果有两层聚合，无论是 GCN 还是 WL test，以蓝色节点为例，先由其二阶邻居信息聚合得到一阶邻居节点信息，再由一阶邻居信息聚合得到自己。

• • 中间图：表示有根的子树结构，WL测试使用它来区分不同的图；
    
  • 右图：如果 GNN 的聚合函数捕获了邻居的 full multiset，那么 GNN 可以以递归的方式捕获有根的子树，其功能与WL测试一样强大；
  • 上图中蓝色节点进行2次WL测试后的标签可以用以蓝色节点为根节点的2层子树来表示；

　　Definition 1 (Multiset). A multiset is a generalized concept of a set that allows multiple instances for its elements. More formally, a multiset is a 2-tuple  $X=(S, m)$  where  $S$  is the underlying set of  $X$  that is formed from its distinct elements, and  $m: S \rightarrow \mathbb{N}_{\geq 1}$  gives the multiplicity of the elements.

　　个人理解：思考 Multiset ，某节点 $v$ 及其邻居集合 $\mathcal{N} (v)$ ，假设节点 $v$ 的 label 是 1 ，其 $\mathcal{N} (v)$ 对应的 label 是 1、1、2、3、4，可以把邻居集合看成一个 Multiset 。[ 我们的目标是使得 $v$ 的表示和 邻居集合中label 为 1 的邻居表示相似。]

　　作者提出 Lemma 2. 说明 WL test 是GNN性能的上限。

　　Lemma 2. Let  $G_{1}$  and  $G_{2}$  be any two non-isomorphic graphs. If a graph neural network  $\mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d}$  maps  $G_{1}$  and  $G_{2}$  to different embeddings, the Weisfeiler-Lehman graph isomorphism test also decides  $G_{1}$  and  $G_{2}$  are not isomorphic.

　　作者提出 Theorem 3：如果 GNN 中 Aggregate、Combine 和 Readout 函数是单射，GNN 可以和 WL test 一样强大。

　　Theorem 3. Let  $\mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d}$  be a  GNN . With a sufficient number of GNN layers,  $\mathcal{A}$  maps any graphs  $G_{1}$  and  $G_{2}$  that the Weisfeiler-Lehman test of isomorphism decides as non-isomorphic, to different embeddings if the following conditions hold:

　　 a) A aggregates and updates node features iteratively with

　　　　$h_{v}^{(k)}=\phi\left(h_{v}^{(k-1)}, f\left(\left\{h_{u}^{(k-1)}: u \in \mathcal{N}(v)\right\}\right)\right)$

　　     where the functions $f$,  which operates on multisets, and $\phi$ are injective(单射). 

 　　b)  $\mathcal{A}$'s graph-level readout, which operates on the multiset of node features $\left\{h_{v}^{(k)}\right\}$ , is injective. 

　　为建模邻居聚合的单射多集函数。下述 Lemma 5.  和 Corollary 6.  为阐述 sum aggregators 是单射的：

　　Lemma 5. Assume $\mathcal{X}$ is countable. There exists a function $f: \mathcal{X} \rightarrow \mathbb{R}^{n}$ so that $h(X)=\sum_{x \in X} f(x)$ is unique for each multiset $X \subset \mathcal{X}$ of bounded size. Moreover, any multiset function g can be decomposed as $g(X)=\phi\left(\sum\limits _{x \in X} f(x)\right)$ for some function $\phi $.

　　Lemma 5.  阐明在 "deep multiset" 和 set 上的一个重要区别是，某些在 set 上是单射的函数并不在 multist 上是单射的 ，如平均聚合器。下面 Corollary 6. 设想表示一个节点及其邻居的通用函数的聚合方案，从而满足 Theorem 3 中的注入条件(a)。

　　Corollary 6. Assume  $\mathcal{X}$  is countable. There exists a function  $f: \mathcal{X} \rightarrow \mathbb{R}^{n}$  so that for infinitely many choices of  $\epsilon$ , including all irrational numbers,  $h(c, X)=(1+\epsilon) \cdot f(c)+\sum\limits _{x \in X} f(x)$  is unique for each pair  $(c, X)$ , where  $c \in \mathcal{X}$  and  $X \subset \mathcal{X}$  is a multiset of bounded size. Moreover, any function $g$ over such pairs can be decomposed as $ g(c, X)=\varphi\left((1+\epsilon) \cdot f(c)+\sum\limits_{x \in X} f(x)\right)$  for some function  $\varphi $.

　　对于 Corollary 6. 引入多层感知机MLP，去学习 $\varphi$ 和 $f$ ，以保证单射性。最终得到基于 MLP+SUM 的 GIN 框架：

　　　　$h_{v}^{(k)}=\operatorname{MLP}^{(k)}\left(\left(1+\epsilon^{(k)}\right) \cdot h_{v}^{(k-1)}+\sum\limits _{u \in \mathcal{N}(v)} h_{u}^{(k-1)}\right)$

　　为什么引入 MLP ，理由：MLP 可以拟合任意函数，故可以拟合出单射函数。

　　在第一次迭代中，如果输入特征是一个 one-hot，那么我们不需要在求加前使用 MLP，因为它们的 SUM 是单射的。

　　通过 GIN 学习的 Node embeddings 可以用于类似于节点分类、连接预测这样的任务。对于图分类任务，文中提出了一个“Readout”函数：给定独立的节点的embeddings，生成整个图的 embedding。

　　Readout 模块使用 concat+sum，对每次迭代得到的所有节点特征求和得到图的特征，然后拼接起来。

　　　　$h_{G}=\operatorname{CONCAT}\left(\operatorname{READOUT}\left(\left\{h_{v}^{(k)} \mid v \in G\right\}\right) \mid k=0,1, \ldots, K\right)$

　　即

　　　　$h_{G}=\operatorname{CONCAT}\left(\operatorname{sum}\left(\left\{h_{v}^{(k)} \mid v \in G\right\}\right) \mid k=0,1, \ldots, K\right)$

 　　本文研究不满足 Theorem 3 的 GraphSAGE 和 GCN，做了两个消融实验：

• • 1-layer perceptrons instead of MLPs .　　
  • mean or max-pooling instead of the sum.　　

　　Lemma 5 中的 $f$ 将不同的 multiset 映射成唯一的 embedding。尽管如此，许多现有的 GNN 反而使用 1-layer perceptron $\sigma \circ W$ ，一个线性映射，然后是一个非线性激活函数，如ReLU。Lemma 7 表明，确实存在一些网络邻域（multisets），而具有一层感知器的模型永远无法区分。

　　Lemma 7. There exist finite multisets  $X_{1} \neq X_{2}$  so that for any linear mapping  $W $,  $\sum\limits_{x \in X_{1}} \operatorname{ReLU}(W x)=\sum\limits_{x \in X_{2}} \operatorname{ReLU}(W x)$.

　　Lemma 7. 的主要思想是，1-layer perceptrons 表现得很像线性映射，因此 GNN 层退化为对邻域特征的简单求和。本文的证明建立在线性映射中缺乏偏差项这一事实之上。有了偏差项和足够大的输出维数，1-layer perceptrons 可能能够区分不同的 multiset。

　　现在考虑将 $h(X)=\sum\limits _{x \in X} f(x)$ 中的 sum 替换为 Mean-pooling 和 Max-pooling 将产生什么问题。

　　Mean-pooling 和 max-pooling aggregators 在某种程度上是一种好的 multiset functions [ 具有平移不变性 ]，但是他们不是单射的。

　　Figure 2 根据三个 aggregators 的表示能力进行了排序。

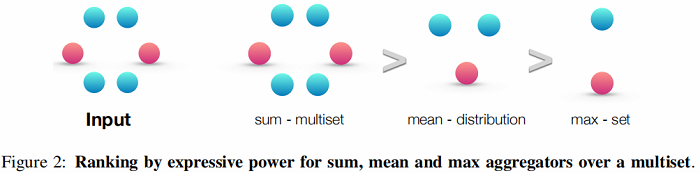
　　三种不同的 Aggregate：

• • sum：学习全部的标签以及数量，可以学习精确的结构信息（不仅保存了分布信息，还保存了类别信息）；[ 蓝色：4个；红色：2 个  ] 
  • mean：学习标签的比例（比如两个图标签比例相同，但是节点有倍数关系），偏向学习分布信息；[ 蓝色：$4/6=2/3$ 的比例；红色：$2/6=1/3$ 的比例  ] 
  • max：学习最大标签，忽略多样，偏向学习有代表性的元素信息；[ 两类（类内相同），所以各一个  ] 

　　Figure 3 说明了mean-pooling aggregators 和 max-pooling aggregators 无法区分的结构对。 

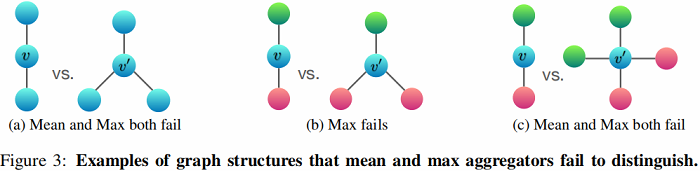
　　在 Figure 3a 中：Every node has the same feature $a$ and $f(a)=h_a$ is the same across all nodes.

• • mean：左 $\frac{1}{2}(h_a+h_a)=h_a$ ，右：$\frac{1}{3}(h_a+h_a+h_a)=h_a$，无法区分；
  • max：左 $h_a$ , 右 $h_a$ 无法区分；
  • sum：左 $2h_a$ , 右 $3h_a$ , 可以区分；

　　在 Figure 3b 中：Let $h_{\text {color }}(r \text { for red, } g \text { for green })$ denote node features transformed by $f $. 

• • mean: 左 $ \frac{1}{2}(h_r+h_g)$ ，右： $\frac{1}{3}(h_g+2h_r) $ ，可以区分；
  • max : 左 $max (h_r, h_g) $ ，右： $max (h_g, h_r, h_r) $ ，无法区分;
  • sum: 左 $sum(h_r+h_g)$ , 右 $sum(2 h_r+h_g)$ , 可以区分；

　　在 Figure 3c 中：

• • mean：左 $\frac{1}{2}(h_r+h_g) $ ，右：$\frac{1}{4}(2 h_g+2 h_r) $ ，无法区分;
  • max：左 $\max (h_g, h_g, h_r, h_r)$ ，右：$\max (h_g, h_r)$ ，无法区分；
  • sum：左 $h_r+h_g$ ，右：$2 h_r+2 h_g$ ，可以区分；

 　　旨在说明等比例 nodes ，使用 mean 是无法区分的。

　　Corollary 8. Assume  $\mathcal{X}$  is countable. There exists a function  $f: \mathcal{X} \rightarrow \mathbb{R}^{n}$  so that for  $h(X)=   \frac{1}{|X|} \sum\limits _{x \in X} f(x), h\left(X_{1}\right)=h\left(X_{2}\right)$  if and only if multisets  $X_{1}$  and  $X_{2}$  have the same distribution. That is, assuming  $\left|X_{2}\right| \geq\left|X_{1}\right| , we have  X_{1}=(S, m)$  and  $X_{2}=(S, k \cdot m)$  for some $k \in \mathbb{N}_{\geq 1}$ .

　　Figure 3 中的示例说明了最大池化考虑的是一个节点与只有一个节点具有相同特性的多个节点（即，将一个 multiset 视为一个集合）。

　　Corollary 9. Assume  $\mathcal{X}$  is countable. Then there exists a function  $f: \mathcal{X} \rightarrow \mathbb{R}^{\infty}$  so that for  $h(X)=\underset{x \in X}{max} f(x), h\left(X_{1}\right)=h\left(X_{2}\right)$  if and only if  $X_{1}$  and  $X_{2}$  have the same underlying set.

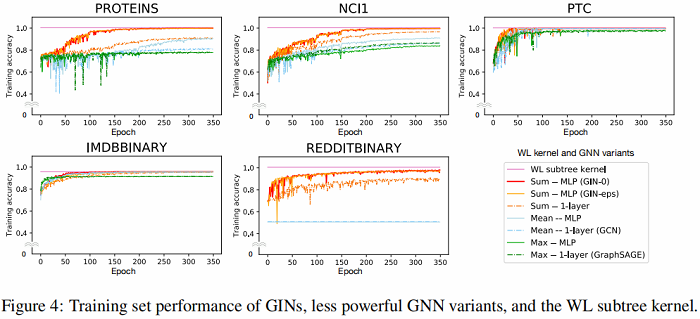
　　在训练中，GIN 和WL test 一样，可以拟合所有数据集，这表说了 GIN 表达能力达到了上限

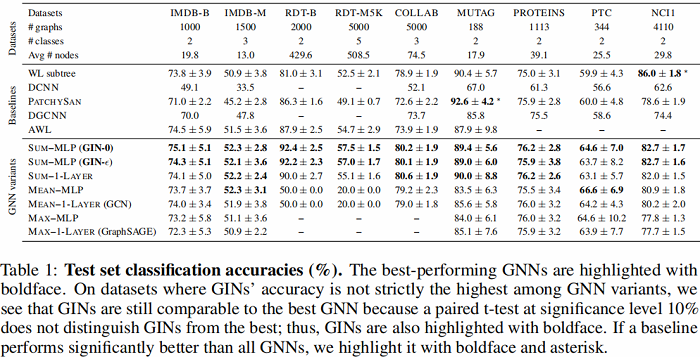
• • GIN-0 比GIN-eps 泛化能力强：可能是因为更简单的缘故；
  • GIN 比 WL test 效果好：因为GIN进一步考虑了结构相似性，即WL test 最终是one-hot输出，而GIN是将WL test映射到低维的embedding；
  • max 在无节点特征的图（用度来表示特征）基本无效；

　　本文主要 基于对 graph分类，证明了 sum 比 mean 、max 效果好，但是不能说明在node 分类上也是这样的效果，另外可能优先场景会更关注邻域特征分布， 或者代表性， 故需要都加入进来实验。

因上求缘，果上努力~~~~