一、线性支持向量机解决的问题
线性可分支持向量机只支持线性可分的训练数据,通过硬间隔最大化实现分类数据;如果训练数据不是线性可分的,我们就需要使用线性支持向量机的方法,去除其中的一些异常点,从而实现剩余样本点的线性可分;相应于硬间隔最大化,它称为软间隔最大化;
二、线性支持向量机的数学模型
为了弥补某些线性不可分样本点的间隔不足的问题,我们为每个样本点引入松弛变量 \(\xi_{i} \geq 0\),从而使得最终的间隔大于等于1
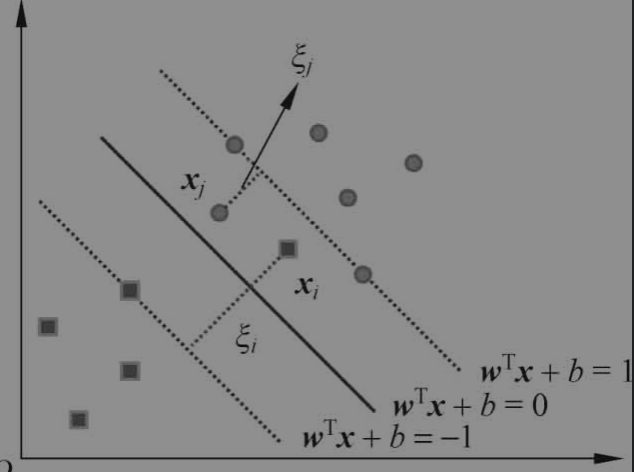
故得到如下约束条件
\[y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i} \]同时目标函数需要计算每个训练样本的松弛量,为了平衡函数间隔和误分类样本点的数量,引入取值为正的惩罚参数C;其值一般由应用问题决定,C值大时对误分类的惩罚增大,C值小时对误分类的惩罚减小;
\[\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \]线性不可分问题的线性支持向量机的学习问题变为如下的凸二次规划问题;
\[\begin{array}{l} \min _{w, b, \xi} \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}\\ s.t. \quad y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\ \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N\\ \end{array} \]通过解决这个优化问题,可以得到超平面
\[w^{*} \cdot x+b^{*}=0 \]分类决策函数
\[f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) \]三、线性支持向量机的对偶算法
模型的原始问题的拉格朗日函数为
\[L(w, b, \xi, \alpha, \mu) \equiv \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} \]对偶问题是拉格朗日函数的极大极小问题。我们首先求L(w,b,ξ,α,µ)对w,b,ξ的极小
\[\begin{array}{l} \nabla_{w} L(w, b, \xi, \alpha, \mu)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0 \\ \nabla_{b} L(w, b, \xi, \alpha, \mu)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ \nabla_{\xi_{i}} L(w, b, \xi, \alpha, \mu)=C-\alpha_{i}-\mu_{i}=0 \end{array} \]通过计算得到
\[\begin{array}{l} w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i} \\ \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ C-\alpha_{i}-\mu_{i}=0 \end{array} \]将以上计算结果带入拉格朗日函数
\[\min _{w, b, \xi} L(w, b, \xi, \alpha, \mu)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \]接着求α的极大,即得对偶问题
\[\begin{array}{l} \max _{\alpha}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i}\\ s.t. \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ 0 \leqslant \alpha_{i} \leqslant C \end{array} \]可以通过求解对偶问题而得到原始问题的解,进而确定分离超平面和决策函数。
设有对偶问题的一个解
如果存在一个分量满足以下条件
\[0<\alpha_{j}^{*} < C \]则可得原始问题的解(b*可能存在多个解)
\[\begin{aligned} w^{*} &=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*} &=y_{j}-\sum_{i=1}^{N} y_{i} \alpha_{i}^{*}\left(x_{i} \cdot x_{j}\right) \end{aligned} \]最终可得超平面和分类决策函数为
\[\begin{array}{l} \sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}=0\\ f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}\right) \end{array} \]四、松弛因子与支持向量
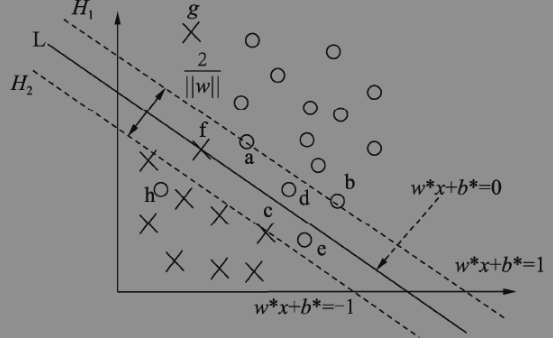
线性支持向量机模型得到的最优超平面如下图所示,与线性可分支持向量机模型相比,线性支持向量机模型中支持向量分为3种
1)分布在间隔边界H1与H2上的样本,此类样本计算的距离得分值刚好等于1,即 \(y_{i}(w^{T}x_{i}+b)=1\),此时松弛因子 \(\xi_{i} = 0\),如样本a、b、c;
2)分布在间隔边界H1与H2之间的样本,如果在间隔内刚好落在分类超平面L上,则\(y_{i}(w^{T}x_{i}+b)=0\),此时的松弛因子\(\xi_{i} = 1\),如样本f;而在间隔边界与超平面L之间时,样本的得分值在0与1之间,即\(0<y_{i}(w^{T}x_{i}+b)<1\),此时的松弛因子\(0<\xi_{i} < 1\),如样本d;如果样本进一步漂移,如样本在超平面L的另一侧,则样本的得分值小于0,即\(-1<y_{i}(w^{T}x_{i}+b)<0\),此时的松弛因子\(1<\xi_{i} < 2\),如样本e;
3)越过间隔边界分布在相反类别区域的样本,则样本的得分小于-1,即\(y_{i}(w^{T}x_{i}+b)<-1\),此时的松弛因子\(\xi_{i}>2\),如样本h、g;
五、合页损失函数,线性支持向量机的另一种解释
支持向量机以函数间隔来衡量分类的准确性,自然也可以合页损失函数来计算损失;当函数间隔大于1的时候,样本分类正确,则损失为0,否则取函数值作为损失;
\[L(y(w\cdot x + b)) = [z]_{+}= [1-y(w\cdot x + b)]_{+} = \left\{\begin{array}{ll} z, & z>0 \\ 0, & z \leqslant 0 \end{array}\right. \]通过加入L2范数正则化得到目标函数为
\[\sum_{i=1}^{N}\left[1-y_{i}\left(w \cdot x_{i}+b\right)\right]_{+}+\lambda\|w\|^{2} \]合页损失函数的图形如下图所示,横轴是函数间隔y(w·x+b),纵轴是损失。由于函数形状像一个合页,故名合页损失函数。
从图中可以看到合页函数是0-1损失函数的上界,它克服了0-1函数非连续可导导致的难以优化的问题;
图中的虚线是感知机的的损失函数(公式如下), 当样本点被正确分类的时候损失值为0,相比之下合页函数不仅要分类正确,还需要足够高的确信度时损失值才是0;
\[\left[-y_{i}\left(w \cdot x_{i}+b\right)\right]_{+} \]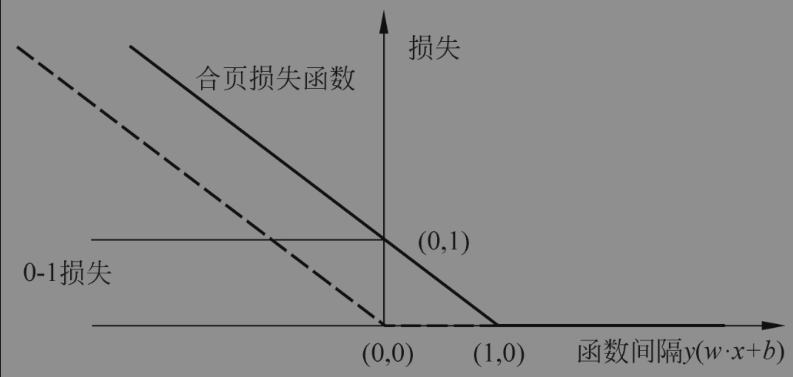
六、算法示例
sklearn提供了LinearSVC类,我们可以通过参数指定C的值,以及使用损失函数;
from sklearn.datasets import load_iris
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
x, y = load_iris(return_X_y= True)
svc = Pipeline([
('scaler',StandardScaler()),
('linear_svc', LinearSVC(C=10, loss='hinge'))
])
svc = svc.fit(x, y)
print(svc.predict(x))
print(svc.score(x, y))
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
# 1 1 1 2 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2]
# 0.9466666666666667
