所谓排序,就是把一个数据群体按个体数据的特征按从大到小或从小到大的顺序存放。
排序在应用开发中很常见,如对商品按价格、人气、购买数量……显示。
初学编程者,刚开始接触的第一个稍微有点难理解的算法应该是排序算法中的冒泡算法。
我初学时,“脑思维”差点绕在 2 个循环结构的世界里出不来了。当时,老师要求我们死记冒泡的口诀,虽然有点搞笑,但是当时的知识层次只有那么点,口诀也许是最好的一种学习方式。
当知识体系慢慢建全,对于冒泡排序的理解,自然也会从形式到本质的理解。
本文先从冒泡排序的本质说起,不仅是形式上理解,而是要做到本质里的理解。
2. 冒泡排序算法所谓冒泡排序算法,本质就是求最大值、最小值算法。
所以,可以暂时抛开冒泡排序,先从最大值算法聊起。
为了更好理解算法本质,在编写算法时不建议直接使用 Python 中已经内置的函数。如
max()、min()……
求最大值,有多种思路,其中最常用的思路有:
- 摆擂台法
- 相邻的两个数字比较法
如一个数列 nums=[3,1,8,9,12,32,7]
算法思想:
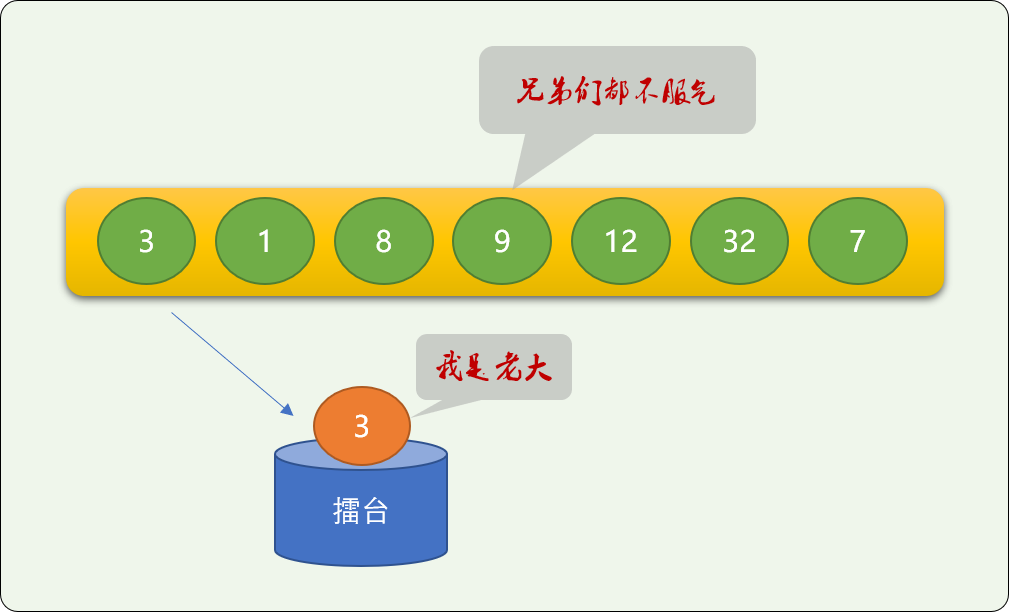
找一个擂台,从数列中随机拎一个数字出来,站在擂台上充当老大。
老大不是说你想当就能当,要看其它的兄弟服不服。于是,其它的数字兄弟会一一登上擂台和擂台上的数字比较,原则是大的留下,小的离开。
如果是找最大值,则是大的留下,小的离开。
反之,如果是找最小值,则是小的留下,大的离开。
你方唱罢我登场。最后留在擂台上的就是真老大了。
nums = [3, 1, 8, 9, 12, 32, 7]
# 第一个数字登上擂台
m = nums[0]
# 其它数字不服气
for i in range(1, len(nums)):
# PK 过程中,大的留在擂台上
if nums[i] > m:
m = nums[i]
# 最后留在擂台上的就是最大值
print("最大值是:", m)
很简单,对不对,如果,找到一个最大值后,再在余下的数字中又找最大值,以此类推,结局会怎样?
最后可以让所有数字都排好序!这就是排序的最本质道理,找着找着就排好序了。
在上面的代码上稍做改动一下,每次找到最大值后存入到另一个列表中。
nums = [3, 1, 8, 9, 12, 32, 7]
# 第一个数字登上擂台
ms=[]
for _ in range(len(nums)):
m = nums[0]
for i in range(1, len(nums)):
if nums[i] > m:
m = nums[i]
# 依次找到的最大值存入新数列
ms.append(m)
# 从原数列中移出找到的最大值,下一轮要在没有它的数列中重新找,不移走,无论找多少次,还会是它
nums.remove(m)
print(ms)
'''
输出结果
[32, 12, 9, 8, 7, 3, 1]
'''
我们可以看到原数列中的数字全部都排序了。但是上述排序算法不完美:
- 另开辟了新空间,显然空间复杂度增加了。
- 原数列的最大值找到后就删除了,目的是不干扰余下数字继续查找最大值。当对所有数字排好序后,原数列也破坏了。
能不能不开辟新空间,在原数列里就完成排序?当然可以。
可以找到最大值就向后移!原数列从逻辑上从右向左缩小。
nums = [3, 1, 8, 9, 12, 32, 7]
# 第一个数字登上擂台
nums_len = len(nums)
for _ in range(len(nums)):
m = nums[0]
for i in range(1, nums_len):
if nums[i] > m:
m = nums[i]
# 最大值找到,移动最后
nums.remove(m)
nums.append(m)
# 这个很关键,缩小原数列的结束位置
nums_len = nums_len - 1
print(nums)
'''
输出结果:
[32, 12, 9, 8, 7, 3, 1]
'''
在原数列上面,上述代码同样完成了排序。
归根结底,上述排序的思路就是不停地找最大值呀、找最大值……找到最后一个数字,大家自然而然就排好序了。
所以算法结构中内层循环是核心找最大值逻辑,而外层就是控制找呀找呀找多少次。
上述排序算法我们也可称是冒泡排序算法,其时间复杂度=外层循环次数X内层循环次数。如有 n 个数字 ,则外层循环 n-1 次,内层循环 n-1 次,在大 O 表示法中,常量可以忽视不计,时间复杂度应该是 O(n2)。
2.2 相邻两个数字相比较如果有 7 个数字,要找到里面的最大值,有一种方案就是每相邻的两个数字之行比较,如果前面的比后面的数字大,则交换位置,否则位置不动。
上体育课的时候,老师排队用的就是这种方式,高的和矮的交换位置,一直到不能交换为此。
nums = [3, 1, 8, 9, 12, 32, 7]
for i in range(len(nums)-1):
# 相邻 2 个数字比较
if nums[i] > nums[i + 1]:
# 如果前面的数字大于后面的数字,则交换
nums[i], nums[i + 1] = nums[i + 1], nums[i]
# 显然,数列最后位置的数字是最大的
print(nums[len(nums) - 1])
'''
输出结果
32
'''
上述代码同样实现了找最大值。
和前面的思路一样,如果找了第一个最大值后,又继续在剩下的数字中找最大值,不停地找呀找,会发现最后所有数字都排好序了。
在上述找最大值的逻辑基础之上,再在外面嵌套一个重复语法,让找最大值逻辑找完一轮又一轮,外层重复只要不少于数列中数字长度,就能完成排序工作,即使外层重复大于数列中数字长度,只是多做了些无用功而已。
nums = [3, 1, 8, 9, 12, 32, 7]
# 外层重复的 100 意味着找了 100 次最大值,这里只是说明问题,就是不停找最大值,显然,是用不着找100 次的
for j in range(100):
for i in range(len(nums)-1):
# 相邻 2 个数字比较
if nums[i] > nums[i + 1]:
# 如果前面的数字大于后面的数字,则交换
nums[i], nums[i + 1] = nums[i + 1], nums[i]
print(nums)
上面的代码就是冒泡排序算法实现。其实冒泡排序就是找了一轮最大值,又继续找最大值的思路。可以对上述算法进行一些优化,如已经找到的最大值没有必要再参与后继的找最大值中去。
显然,找最大值的最多轮数是数列长度减 1 就可以了。5 个数字,前面 4 个找到了,自然大家就都排好序了。
nums = [3, 1, 8, 9, 12, 32, 7]
# 找多少次最大值,数列长度减 1
for j in range(len(nums)-1):
for i in range(len(nums)-1-j):
# 相邻 2 个数字比较
if nums[i] > nums[i + 1]:
# 如果前面的数字大于后面的数字,则交换
nums[i], nums[i + 1] = nums[i + 1], nums[i]
print(nums)
在学习冒泡排序算法时,不要被外层、内层循环结构吓住,核心是理解求最大值算法。上述冒泡排序算法的时间复杂度也是 O(n2)。
3. 选择排序算法选择排序算法是冒泡排序的变种,还是在找最大(小)值算法,冒泡排序是一路比较一路交换,为什么要这样,因为不知道数列中哪一个数字是最大(小)值,所以只能不停的比较不停的交换。
选择排序有一个优于冒泡的理念,需要交换时才交换。
所以选择排序算法的问题就是什么时候需要交换?
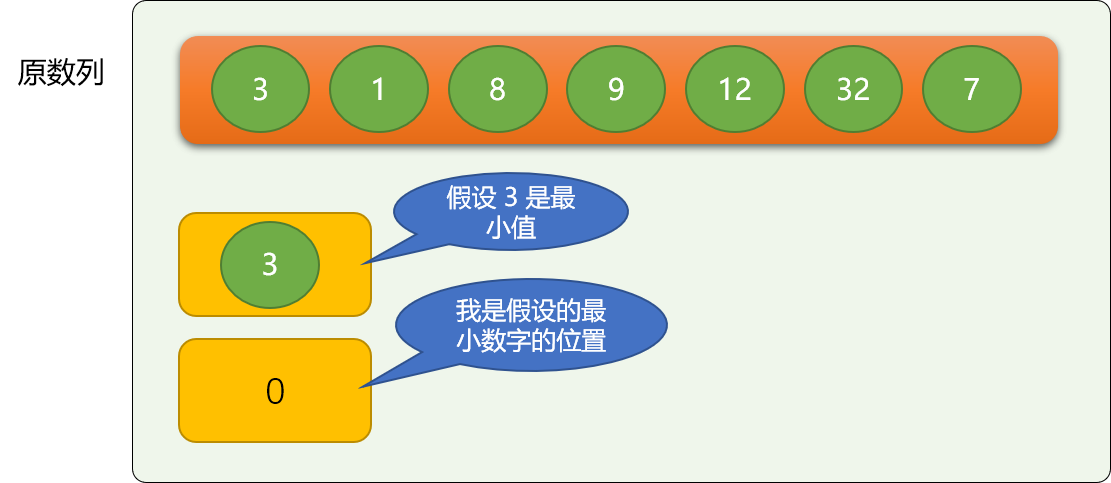
选择排序先是假设第一个数字是最小值,然后在后面的数字里找有没有比这个假设更小的。不是说,找一个小的就交换,因为有可能还有比之更小的,只有当后续所有数字找完后,再确定进行交换,
还是使用擂擂台算法实现找最大(小)值,找到后交换位置。
nums = [6, 2, 5, 9, 12, 1, 7]
# 擂台!假充第一 个数字是最小值
mi = nums[0]
# 假设的最小数字位置
mi_idx = 0
# 真正最小数字的位置
real_idx = mi_idx
for i in range(mi_idx + 1, len(nums)):
if nums[i] < mi:
mi = nums[i]
# 记住更小数字的位置,不记着交换
real_idx = i
# 如有更小的
if real_idx != mi_idx:
# 交换
nums[real_idx], nums[mi_idx] = nums[mi_idx], nums[real_idx]
print(nums)
'''
输出结果
[1, 2, 5, 9, 12, 6, 7]
'''
以上代码就是选择排序的核心逻辑,实现了把最小的数字移动最前面。
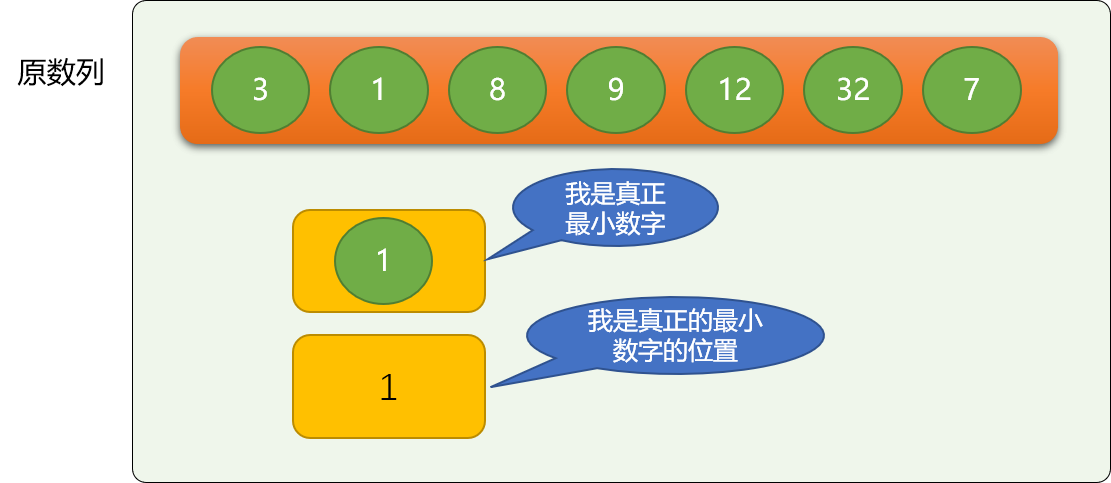
再在上述逻辑基础上,继续在后续数字中找出最小值,并移动前面。多找几次就可以了!本质和冒泡算法还是一样的,不停找最大(小)值。
nums = [6, 2, 5, 9, 12, 1, 7]
for j in range(len(nums)-1):
mi = nums[j]
# 假设的最小数字位置
mi_idx = j
# 真正最小数字的位置
real_idx = mi_idx
for i in range(mi_idx + 1, len(nums)):
if nums[i] < mi:
mi = nums[i]
# 记住更小数字的位置
real_idx = i
# 如有更小的
if real_idx != mi_idx:
# 交换
nums[real_idx], nums[mi_idx] = nums[mi_idx], nums[real_idx]
print(nums)
'''
输出结果:
[1, 2, 5, 6, 7, 9, 12]
'''
选择排序的时间复杂度和冒泡排序的一样 O(n2)。
4. 插入排序打牌的时候,我们刚拿到手上的牌是无序的,在整理纸牌并让纸牌一步一步变得的有序的过程就是插入算法的思路。
插入排序的核心思想:
-
把原数列从逻辑(根据起始位置和结束位置在原数列上划分)上分成前、后两个数列,前面的数列是有序的,后面的数列是无序的。
刚开始时,前面的数列(后面简称前数列)只有唯一的一个数字,即原数列的第一个数字。显然是排序的!
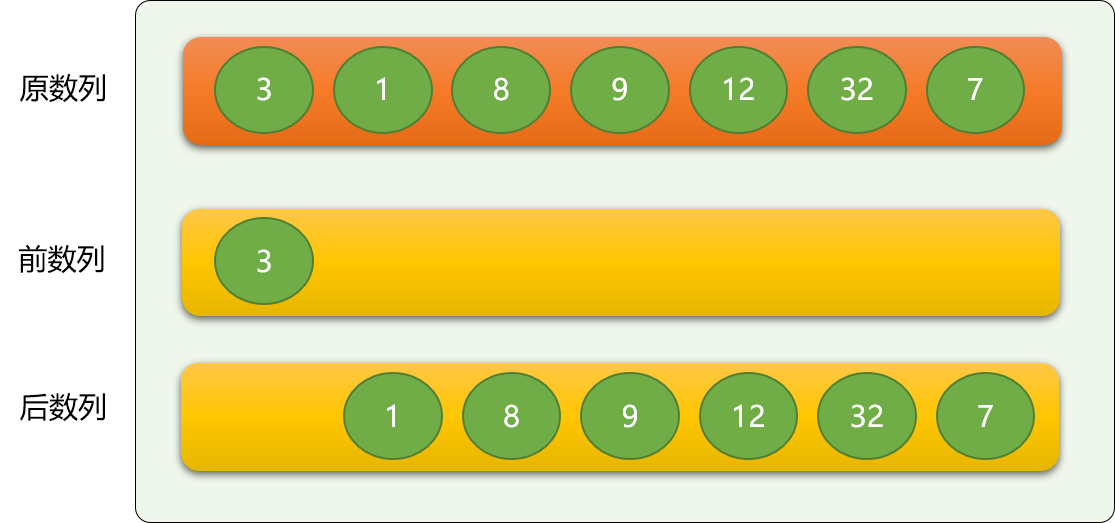
-
依次从后数列中逐个拿出数字,与前数列的数字进行比较,保证插入到前数列后,整个前数列还是有序的。
如上,从后数列中拿到数字 1 ,然后与前数字的 3 进行比较,如果是从大到小排序,则 1 就直接排到 3 后面,如果是从小到大排序,则 1 排到 3 前面。
这里,按从小到大排序。
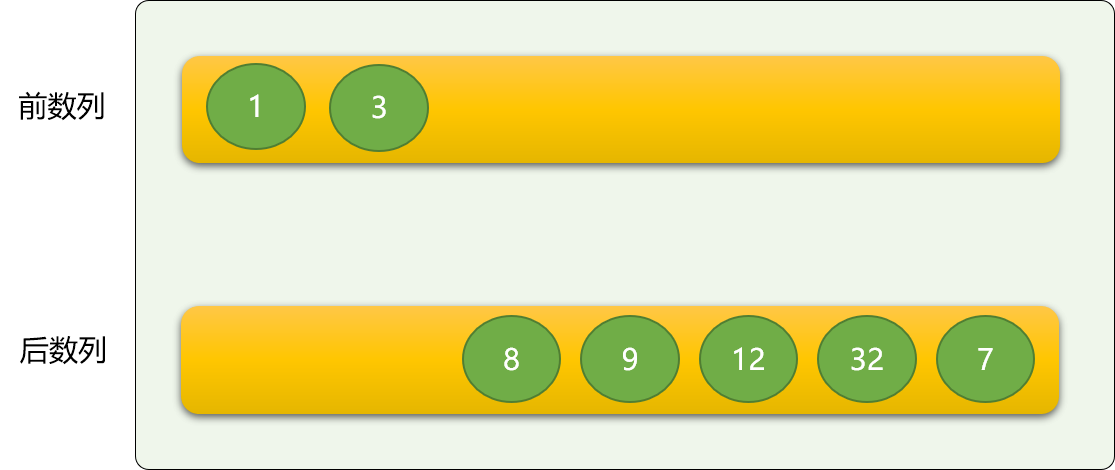
从如上描述可知,插入排序核心逻辑是:
- 比较: 后数列的数字要与前数字的数字进行大小比较,这个与冒泡和选择排序没什么不一样。
- 移位: 如果前数列的数字大于后数列的数字,则需要向后移位。也可以和冒泡排序一样交换。
- 插入: 为后数列的数字在前数列中找到适当位置后,插入此数据。
插入排序的代码实现:
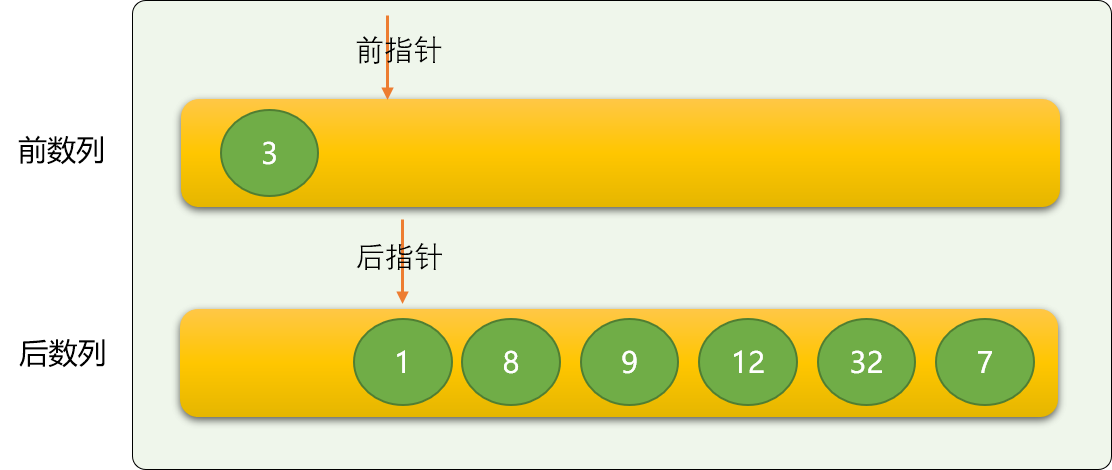
这里使用前指针和后指针的方案。
-
前指针用来在前数列中定位数字,方向是从右向左。
-
后指针用来在后数字中定位数字,方向是从左向右。
前指针初始的位置之前为前数列,后指针初始时的位置为后数列。

nums = [3, 1, 8, 9, 12, 32, 7]
# 后指针指向原数列的第 2 个数字,所以索引号从 1 开始
for back_idx in range(1, len(nums)):
# 前指针和后指针的关系,
front_idx = back_idx - 1
# 临时变量,比较时,前数列的数字有可能要向后移位,需要把后指针指向的数字提前保存
tmp = nums[back_idx]
# 与前数列中的数字比较
while front_idx >= 0 and tmp < nums[front_idx]:
# 移位
nums[front_idx + 1] = nums[front_idx]
front_idx -= 1
if front_idx != back_idx - 1:
# 插入
nums[front_idx + 1] = tmp
print(nums)
'''
输出结果
[1,3,7,8,9,12,32]
'''
上述代码用到了移位和插入操作,也可以使用交换操作。如果是交换操作,则初始时,前、后指针可以指向同一个位置。
nums = [3, 1, 8, 9, 12, 32, 7]
for back_idx in range(1, len(nums)):
for front_idx in range(back_idx, 0, -1):
if nums[front_idx] < nums[front_idx - 1]:
nums[front_idx], nums[front_idx - 1] = nums[front_idx - 1], nums[front_idx]
else:
break
print(nums)
后指针用来选择后数列中的数字,前指针用来对前数列相邻数字进行比较、交换。和冒泡排序一样。
这里有一个比冒泡排序优化的地方,冒泡排序需要对数列中所有相邻两个数字进行比较,不考虑是不是有必要比较。
但插入不一样,因插入是假设前面的数列是有序的,所以如果后指针指向的数字比前数列的最后一个数字都大,显然,是不需要再比较下去,如下的数字 `` 是不需要和前面的数字进行比较,直接放到前数列的尾部。
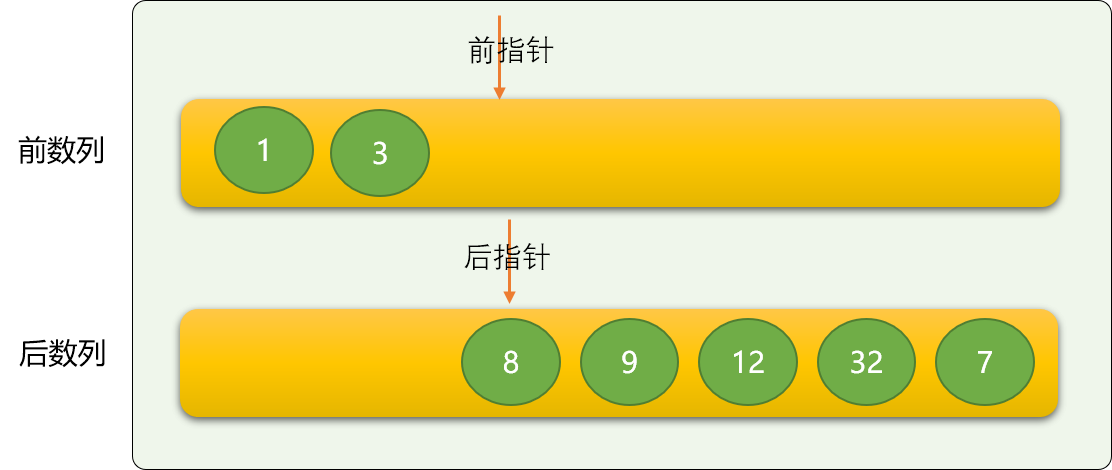
插入排序的时间复杂度还是 O(n2) 。
5. 快速排序快速排序是一个很有意思的排序算法,快速排序的核心思想:
-
分治思想: 全局到局部、或说是粗糙到完美的逐步细化过程。
类似于画人物画。
先绘制一个轮廓图,让其看起来像什么!
然后逐步细化,让它真的就是什么!
快速排序也是这个思想,刚开始,让数列粗看起来有序,通过逐步迭代,让其真正有序。
-
二分思想: 在数列选择一个数字(基数)为参考中心,数列比基数大的,放在左边(右边),比基数小的,放在右边(左边)。
第一次的二分后:整个数列在基数之上有了有序的轮廓,然后在对基数前部分和后部分的数字继续完成二分操作。
这里使用左、右指针方式描述快速排序:
- 左指针初始指向最左边数字。
- 右指针初始指向最右边数字。
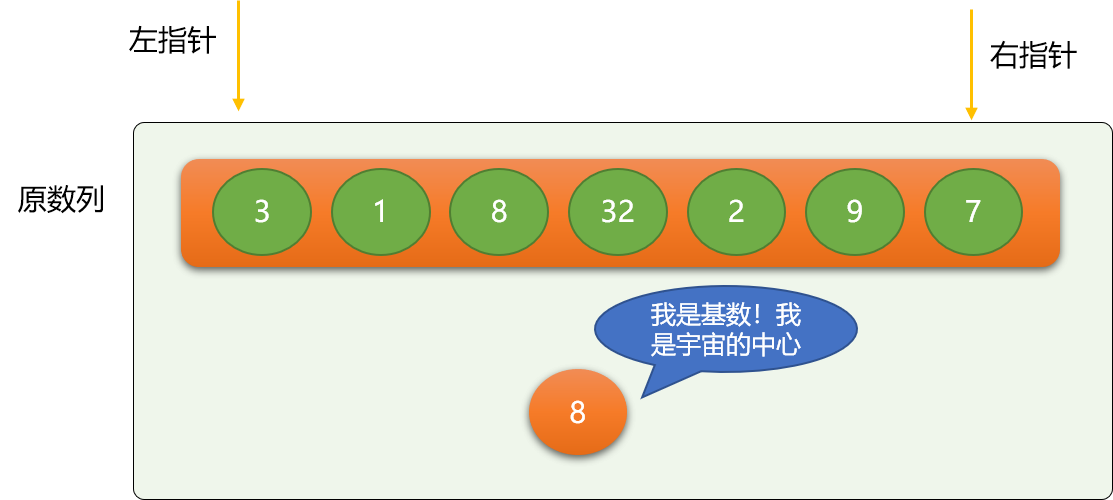
这里选择 8 作为第一次二分的基数,基数的选择没有特定要求,只要是数列中的数字,别客气,任意选择。这里把比 8 小的移到 8 的左边,比 8 大的移动 8 的右边。
移位的流程:
- 左指针不停向右移动,至到遇到大于等于基数的数字 ,同理右指针不停向左移动,至到碰到小于等于基数的数字。
- 交换左指针和右指针的位置的数据。
如上图,左指针最后会停止在数字 8 所在位置,右指针会停在数字 7 所在位置。
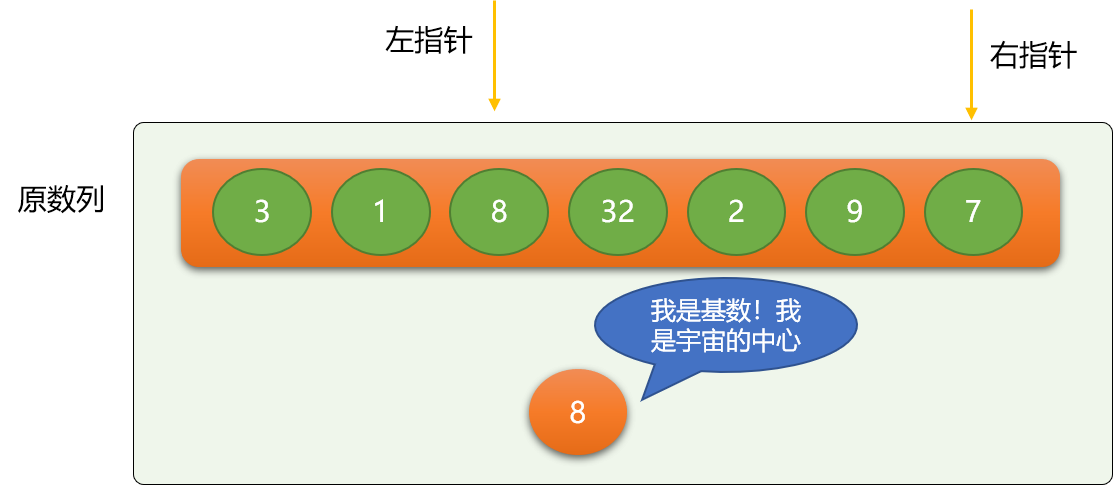
交换左、右指针位置的数字。
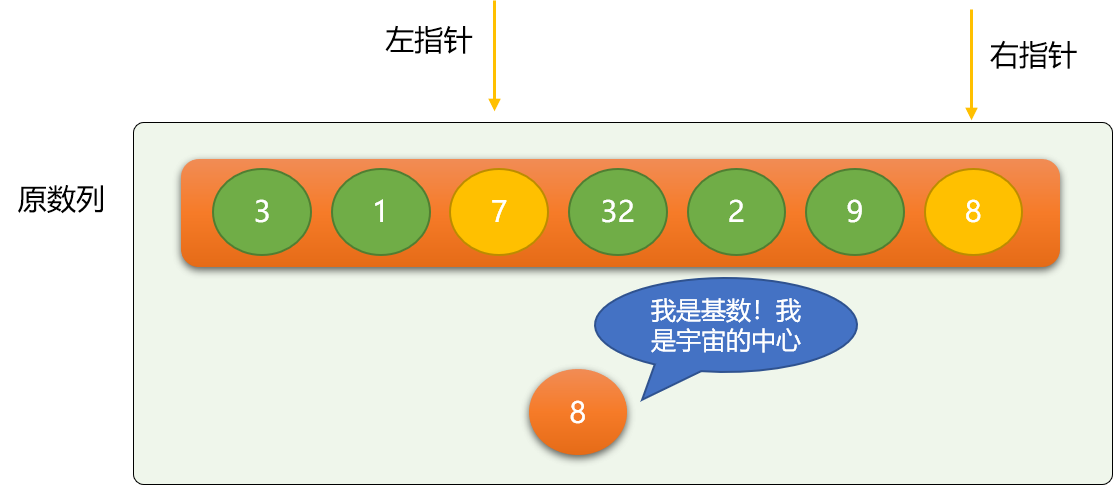
依此类推,继续移动指针、交换。
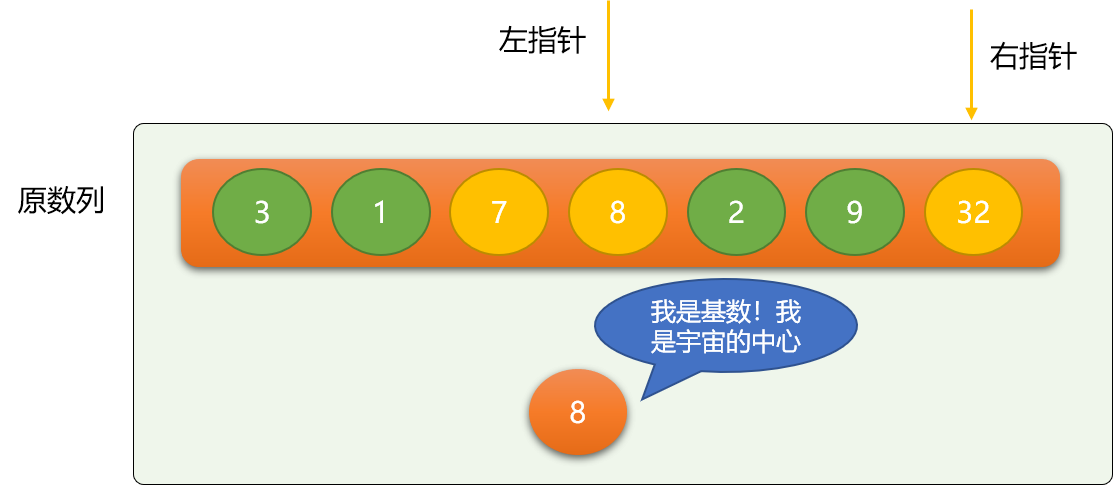
第一次二分后,整个数列会变成如下图所示:
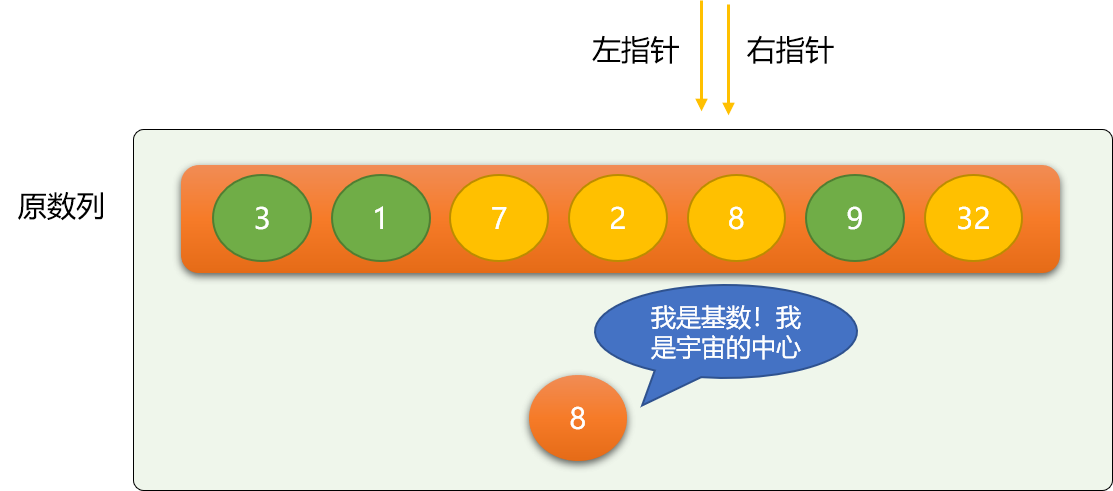
当左、右指针重合在一起时,第一次二分过程到此结束。以基数 8 为分界线,把原数列分成前、后两部分,继续在前、后数列上面使用如上二分思想 。显然,使用递归是最直接有效的选择。
如下第一次二分代码:
nums = [3, 1, 8, 32, 2, 9, 7]
def quick_sort(nums):
# 左指针
left = 0
# 右指针
right = len(nums) - 1
# 基数,可以是任意数字,一般选择数列的第一个数字
base_n = 8
while left < right:
# 左指针向右移动,至到时左指针位置数字大于等于基数,
while nums[left] < base_n and left < right:
left += 1
while nums[right] > base_n and right > left:
right -= 1
# 交换
nums[left], nums[right] = nums[right], nums[left]
quick_sort(nums)
print(nums)
输出结果:
[3, 1, 7, 2, 8, 9, 32]
和上面的演示流程图的结果一样。
使用递归进行多次二分:
nums = [3, 1, 8, 32, 2, 9, 7]
def quick_sort(nums, start, end):
if start >= end:
return
# 左指针
left = start
# 右指针
right = end
# 基数
base_n = nums[start]
while left < right:
while nums[right] > base_n and right > left:
right -= 1
# 左指针向右移动,至到时左指针位置数字大于等于基数,
while nums[left] < base_n and left < right:
left += 1
# 交换
nums[left], nums[right] = nums[right], nums[left]
# 左边数列
quick_sort(nums, start, left - 1)
# 右边数列
quick_sort(nums, right + 1, end)
quick_sort(nums, 0, len(nums) - 1)
print(nums)
'''
输出结果
[1, 2, 3, 7, 8, 9, 32]
'''
快速排序的时间复杂度为 O(nlogn),空间复杂度为O(nlogn)。
6. 总结除了冒泡、选择、插入、快速排序算法,还有很多其它的排序算法,冒泡、选择 、插入算法很类似,有其相似的比较、交换逻辑。快速排序使用了分治理念,可从减少时间复杂度。
