1、K-近邻算法(KNN)1.1 定义 (KNN,K-NearestNeighbor) 如果一个样本在特征空间中的 k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别 ,则该样本也属于这个类别。 1.2 距离
(KNN,K-NearestNeighbor)
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
1.2 距离公式两个样本的距离可以通过如下公式计算,又叫欧式距离。
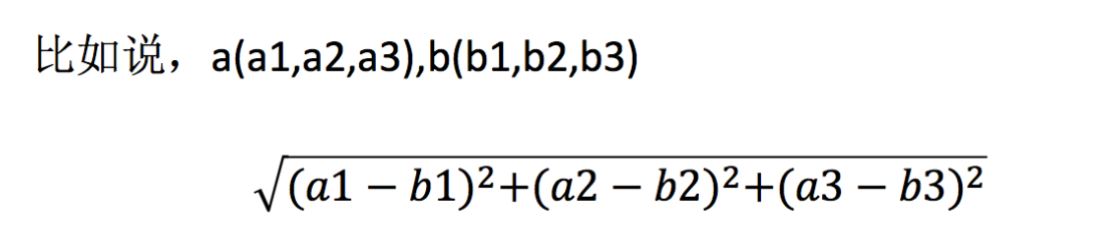
简单理解这个算法:
这个算法是用来给特征值分类的,是属于有监督学习的领域,根据不断计算特征值和有目标值的特征值的距离来判断某个样本是否属于某个目标值。
可以理解为根据你的邻居来判断你属于哪个类别。
1.3 API- sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
- 其中的你指定的邻居个数实际上是指的当算法计算完一个样本的特征值距离所有其他样本的目标值的距离之后,会根据距离的大小排序,而你的指定的这个参数就是取前多少个值作为判定依据。
- 比如说你指定邻居是5那么如果5个邻居里3个是爱情片,那么可以说这个样本属于爱情片。
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import pandas as pd
def knncls():
"""
K近邻算法预测入住位置类别
row_id,x,y,accuracy,time,place_id
用户ID,坐标x,坐标y,准确度,时间,位置ID
:return:
"""
# 一、处理数据以及特征工程
# 1、读取收,缩小数据的范围
data = pd.read_csv("./train.csv")
# 数据逻辑筛选操作 df.query()
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
# 删除time这一列特征
data = data.drop(['time'], axis=1)
print(data)
# 删除入住次数少于三次位置
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
# 3、取出特征值和目标值
y = data['place_id']
# y = data[['place_id']]
x = data.drop(['place_id', 'row_id'], axis=1)
# 4、数据分割与特征工程?
# (1)、数据分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
# (2)、标准化
std = StandardScaler()
# 队训练集进行标准化操作
x_train = std.fit_transform(x_train)
print(x_train)
# 进行测试集的标准化操作
x_test = std.fit_transform(x_test)
# 二、算法的输入训练预测
# K值:算法传入参数不定的值 理论上:k = 根号(样本数)
# K值:后面会使用参数调优方法,去轮流试出最好的参数[1,3,5,10,20,100,200]
knn = KNeighborsClassifier(n_neighbors=1)
# 调用fit()
knn.fit(x_train, y_train)
# 预测测试数据集,得出准确率
y_predict = knn.predict(x_test)
print("预测测试集类别:", y_predict)
print("准确率为:", knn.score(x_test, y_test))
return None
if __name__ == '__main__':
print()
返回结果:
row_id x y accuracy place_id
600 600 1.2214 2.7023 17 6683426742
957 957 1.1832 2.6891 58 6683426742
4345 4345 1.1935 2.6550 11 6889790653
4735 4735 1.1452 2.6074 49 6822359752
5580 5580 1.0089 2.7287 19 1527921905
... ... ... ... ... ...
29100203 29100203 1.0129 2.6775 12 3312463746
29108443 29108443 1.1474 2.6840 36 3533177779
29109993 29109993 1.0240 2.7238 62 6424972551
29111539 29111539 1.2032 2.6796 87 3533177779
29112154 29112154 1.1070 2.5419 178 4932578245
[17710 rows x 5 columns]
[[-0.39289714 -1.20169649 0.03123826]
[-0.52988735 0.71519711 -0.08049297]
[ 0.84001481 0.82113447 -0.73225846]
...
[-0.64878452 -0.59040929 -0.20153513]
[-1.37250642 -1.33053923 -0.44361946]
[-0.11503962 -1.30477068 -0.22946794]]
预测测试集类别: [4932578245 3312463746 8048985799 ... 1285051622 2199223958 6780386626]
准确率为: 0.4034672970843184
Process finished with exit code 0
knn.fit(x_train, y_train)
用x_train, y_train训练模型
模型训练好之后
y_predict = knn.predict(x_test)
调用预测方法预测x_test的结果
计算准确率
print("准确率为:", knn.score(x_test, y_test))
补充估计器estimator工作流程
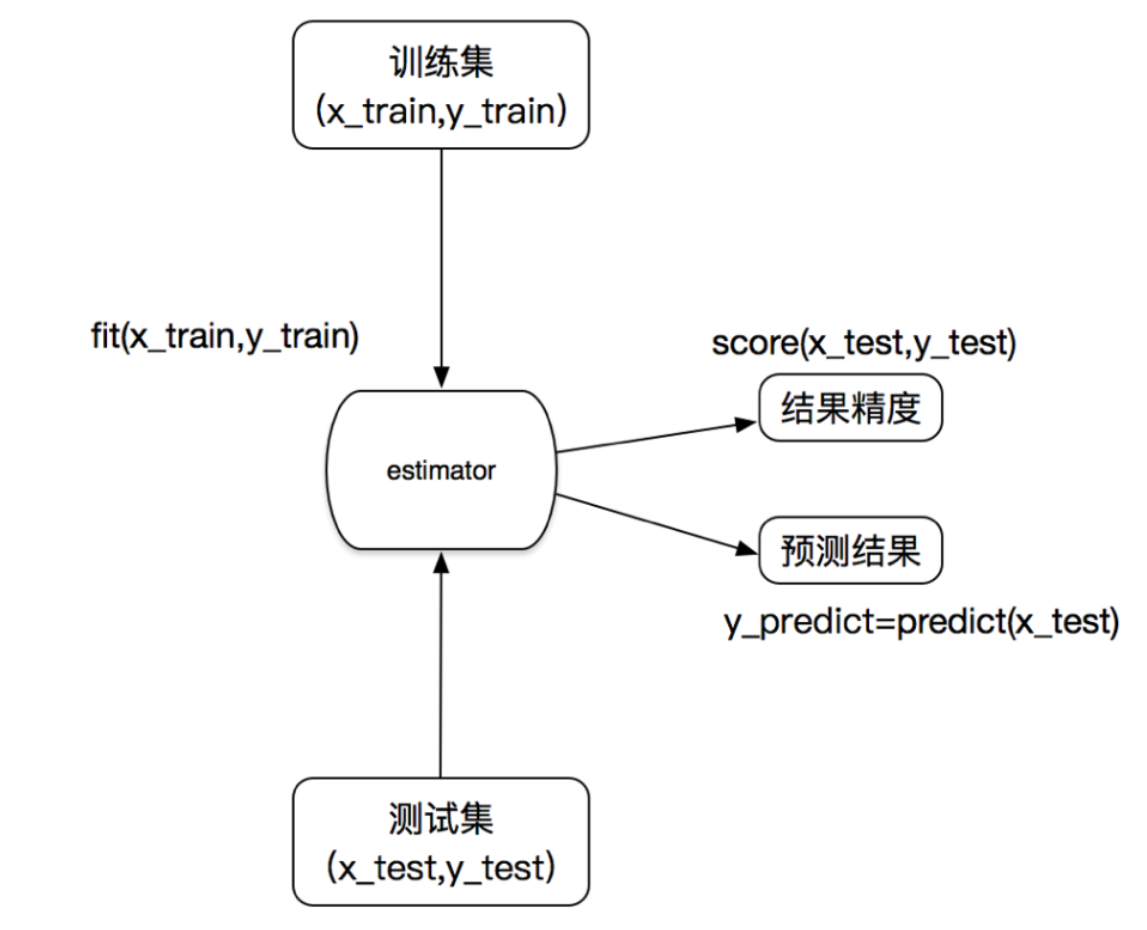
- 1、k值取多大?有什么影响?
k值取很小:容易受到异常点的影响,比如说有异常的邻居出现在你旁边,那么你的计算结果就会很大程度地受其影响。
k值取很大:受到样本均衡的问题,k值过大相当于选的参考邻居太多了,以至于不知道选哪一个作为标准才好。
- 2、性能问题?
距离计算,时间复杂度高
小结:- 优点:
- 简单,易于理解,易于实现,无需训练
- 缺点:
- 懒惰算法,对测试样本分类时的计算量大,内存开销大
- 必须指定K值,K值选择不当则分类精度不能保证
- 使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试
2、交叉验证(cross validation)
交叉验证:将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成4份,其中一份作为验证集。然后经过4次(组)的测试,每次都更换不同的验证集。即得到4组模型的结果,取平均值作为最终结果。又称4折交叉验证。
2.1 分析我们之前知道数据分为训练集和测试集,但是为了让从训练得到模型结果更加准确。做以下处理
- 训练集:训练集+验证集
- 测试集:测试集

通常情况下,有很多参数是需要手动指定的(如k-近邻算法中的K值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
- sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
- 对估计器的指定参数值进行详尽搜索
- estimator:估计器对象
- param_grid:估计器参数(dict){“n_neighbors”:[1,3,5]}
- cv:指定几折交叉验证
- fit:输入训练数据
- score:准确率
- 结果分析:
- bestscore:在交叉验证中验证的最好结果_
- bestestimator:最好的参数模型
- cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果
简单理解:就是在训练的时候随机选一组数据做自身验证,然后去比较哪次的结果好一些,就选这个训练的模型作为结果!
2.3 案例(KNN算法---鸢尾花分类)def knn_iris_gscv():
"""
用KNN算法对鸢尾花进行分类,添加网格搜索和交叉验证
:return:
"""
# 1)获取数据
iris = load_iris()
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3)特征工程:标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4)KNN算法预估器
estimator = KNeighborsClassifier()
# 加入网格搜索与交叉验证
# 参数准备 n可能的取值 用字典表示 cv = ? 表示几折交叉验证
param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)
estimator.fit(x_train, y_train)
# 5)模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 最佳参数:best_params_
print("最佳参数:\n", estimator.best_params_)
# 最佳结果:best_score_
print("最佳结果:\n", estimator.best_score_)
# 最佳估计器:best_estimator_
print("最佳估计器:\n", estimator.best_estimator_)
# 交叉验证结果:cv_results_
print("交叉验证结果:\n", estimator.cv_results_)
return None
返回结果:
y_predict:
[0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
最佳参数:
{'n_neighbors': 3}
最佳结果:
0.9553030303030303
最佳估计器:
KNeighborsClassifier(n_neighbors=3)
交叉验证结果:
{'mean_fit_time': array([0.00059769, 0.0005955 , 0.00069804, 0.00039876, 0.00049932,
0.00039904]), 'std_fit_time': array([0.00048802, 0.00048625, 0.00063848, 0.00048837, 0.00049932,
0.00048872]), 'mean_score_time': array([0.00144098, 0.00109758, 0.00109758, 0.00089834, 0.00109644,
0.00089748]), 'std_score_time': array([0.00047056, 0.00030139, 0.00029901, 0.0005389 , 0.00029947,
0.00029916]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
mask=[False, False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([0.91666667, 0.91666667, 1. , 1. , 0.91666667,
0.91666667]), 'split1_test_score': array([1., 1., 1., 1., 1., 1.]), 'split2_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split3_test_score': array([0.90909091, 1. , 0.90909091, 0.90909091, 0.90909091,
1. ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split6_test_score': array([0.90909091, 0.90909091, 0.90909091, 1. , 1. ,
1. ]), 'split7_test_score': array([0.90909091, 0.90909091, 0.81818182, 0.81818182, 0.81818182,
0.81818182]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([1., 1., 1., 1., 1., 1.]), 'mean_test_score': array([0.94621212, 0.95530303, 0.94545455, 0.95454545, 0.94621212,
0.95530303]), 'std_test_score': array([0.04397204, 0.0447483 , 0.06030227, 0.06098367, 0.05988683,
0.0604591 ]), 'rank_test_score': array([4, 1, 6, 3, 4, 1])}
垃圾邮件分类:
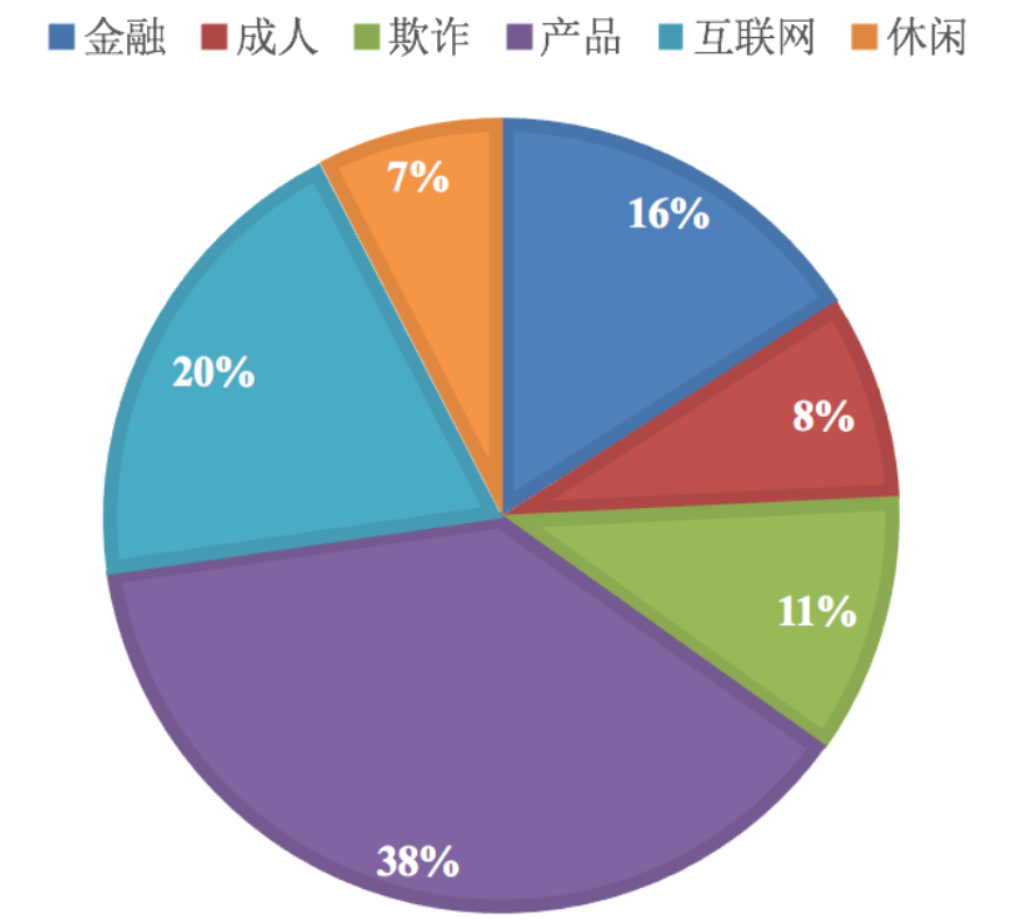
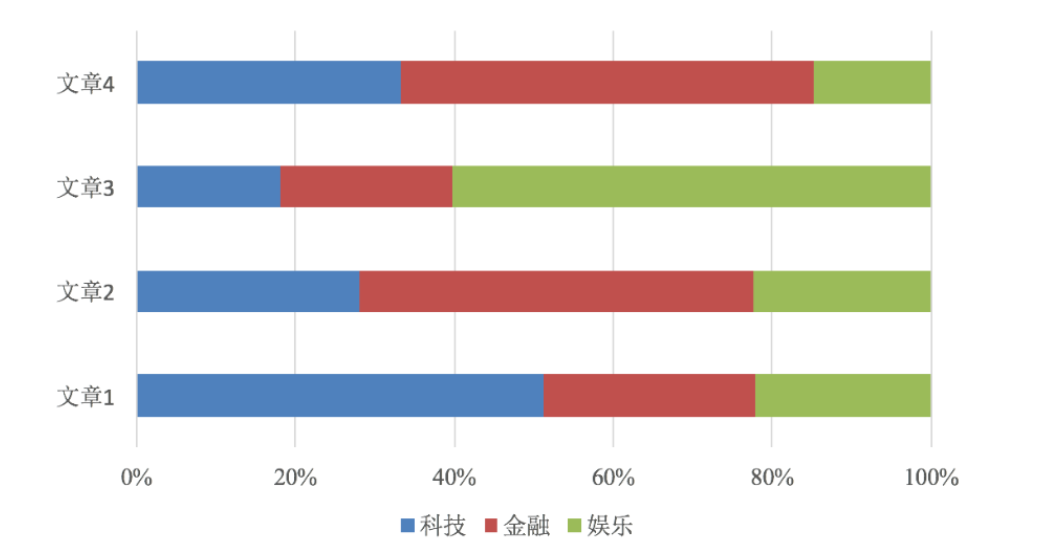

公式分为三个部分:
- P(C):每个文档类别的概率(某文档类别数/总文档数量)
- P(W│C):给定类别下特征(被预测文档中出现的词)的概率
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- Ni为该F1词在C类别所有文档中出现的次数
- N为所属类别C下的文档所有词出现的次数和
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- P(F1,F2,…) 预测文档中每个词的概率

朴素贝叶斯即假定所有的特征值之间相互独立
3.2 文档分类计算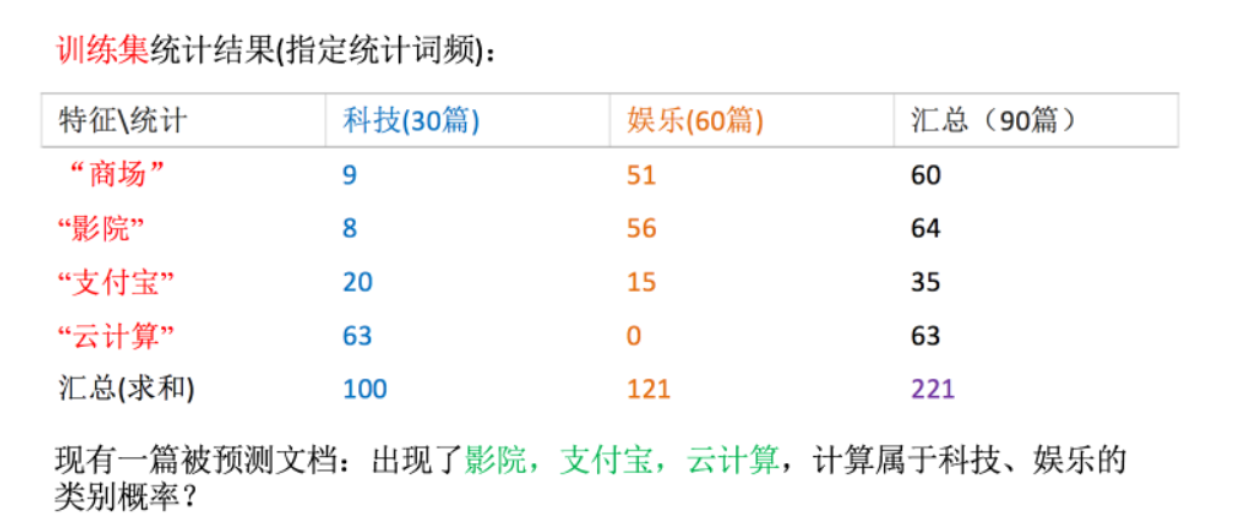
科技:P(科技|影院,支付宝,云计算) = 