模块化编程是 Python 的基本思想。初学 Python,都应该使用过小海龟、随机、数学模块。使用模块之前,需要导入模块,然后根据自己的问题需要使用这些模块。
Python 提供了大量的模块库,这些模块中有 Python 语言系统自带的、也有第三方提供的、也可以由开发者根据需要创建。
内置模块,直接拿来使用就可以。
第三方模块,需要使用 Python 自带的安装程序 pip(pip3 是 pip 的升级版本) 安装。
pip3 install 模块
pip 或 pip3 是命令行程序。使用之前,需要进入 OS 的命令模式。windows 操作系统中使用 win+r 打开运行对话框,输入 cmd ,进入命令操作模式 。
命令模式下直接输入 pip3,便可出现如下 pip3 的基本功能(前提需要安装 Python 运行环境)。
Commands:
install 安装模块
download 下载模块
uninstall 卸载模块
list 列表出安装的模块
show 显示安装模块的信息
check 验证模块的依赖信息
config 管理本地和全局配置
search 从 PyPI (Python Package Index 是 Python 编程语言的软件存储库) 搜索模块
index 使用模块的索引检查模块的合法性
什么是模块化编程?
Python 语言系统中一个文件就是一个模块,一个模块中可以封装很多实用的功能代码,这些功能体可以以函数的形式存在,也可以以类的形式存存,模块具有完全的自我独立性。
模块与模块之间可以在需要时相互依赖。
模块化编程可以大大提高代码的重用性,也可以无限扩展 Python 语言的功能。Python 经过多年的积累和沉淀,已经有诸多丰富的模块可以使用。
2. 函数Python 语言中,函数是一等公民。
函数定义语法结构:
def 函数名(函数参数):
函数体
- 定义函数,也就是创建一个函数必须使用 def 关键字。
- 函数名是函数的唯一标识符,也是使用函数的接口(入口)。
- 函数参数:用来接收调用者传过来的数据变量。也称为形式参数(占位符)。参数可以没有,也可以有多个。
- 函数体:函数提供的功能实现。
Python 函数的特点:
Python 既是面向对象编程语言,也是面向函数的编程语言。函数可以作为其它函数的参数,也可以作为其它函数的返回值。函数本质是一种数据类型。
def han_shu():
print(1)
print(type(han_shu))
'''
输出结果:
<class 'function'>
'''
有些时候,称类中函数为方法。只是语义上的区别,本质一样。
创建函数意味着根据 function 类型创建一个 function 对象。
- 函数作为参数:
def a_han_shu(f):
f()
def b_han_shu():
print('Test')
# 函数作为参数不要有括号。
a_han_shu(b_han_shu)
'''
输出结果
Test
'''
- 函数作为返回值:
def a_han_shu():
def b_han_shu():
print('Test')
return b_han_shu
# 返回的是对 b_han_shu 函数的引用
f=a_han_shu()
f()
'''
输出结果
Test
'''
无论是使用函数作为参数还是返回值,函数不能有括号。
当函数后面有括号,意味着是执行函数中的逻辑代码。
- 使用其它模块中的函数作参数:
import turtle
def forward(f):
f(200)
# turtle.forward 后面不能有括号
forward(turtle.forward)
'''
用自己的函数封装小海龟的前移函数
'''
- 类的方法本质还是函数
class Dog:
def __init__(self, name):
self.name = name
def run(self):
print(self.name,"在 run……")
def bark(self, f):
f()
print(self.name,"在 叫……")
d = Dog('小花')
d.bark(d.run)
'''
输出结果
小花 在 run……
小花 在 叫……
'''
函数的参数形式:
- 位置传递参数:
def han_shu(num1, num2):
return num1 - num2
#如果想得到 10-4 相减的结果,调用时 10,4 的顺序不能颠倒。如果传递4,10 得到 4-10 结果
res = han_shu(10, 4)
print(res)
'''
输出结果
6
'''
- 命名传递参数:
def han_shu(num1, num2):
return num1 - num2
#通过参数名传递数据
res = han_shu(num1=10,num2=4)
print(res)
# 传递参数时可以颠倒顺序
res = han_shu(num2=4,num1=10)
print(res)
'''
输出结果
6
'''
- 默认值传递
def han_shu(num1, num2=4):
return num1 - num2
#通过参数名传递数据
res = han_shu(10)
print(res)
'''
输出结果
6
'''
切记:默认值参数只能放在最后。
- 可变长度参数
def han_shu(*num):
return num
res = han_shu(10, 4,6,12)
print(res)
'''
输出结果
(10, 4, 6, 12)
'''
参数前面的 * 表示可以传递 0 个、1 个或多个参数,函数内部会把所有传过来的数据放在一个元组中。
def han_shu(**num):
return num
res = han_shu(a=1,b=2,c=3)
print(res)
'''
输出结果
{'a': 1, 'b': 2, 'c': 3}
'''
参数前面的 ** 表示可以接收任意多的以键、值对形式的参数。函数内部用字典的形式存储传过来的数据。
匿名函数
匿名函数也称为 lambda 函数,是对函数语法的简化。lambda 函数有如下几个特点:
- 没有函数名。
- 只能使用一次。
- 只能有一句函数体。
- 不能有 return 语句,默认返回唯一语句块的计算结果。
def han_shu():
return lambda num: num + 1
res = han_shu()
print(res(12))
'''
输出结果
13
'''
上面的 han_shu 函数会返回一个匿名函数的引用。相当于下面的代码:
def han_shu():
def f(num):
return num + 1
return f
res = han_shu()
print(res(12))
'''
输出结果
'''
内置函数:
Python 中有很多内置函数、或称为系统函数,此类函数特点:可以直接使用。
常用内置函数:
递归指函数自己调用自己。递归调用有 2 个过程:
1、递进过程:如有一个函数 a 。递归调用过程:第一次调用 a ===> 第二次调用 a ===>第三次调用 a => ……=>第 n 次调用 a。如果没有任何中止条件,则会无限制推进,导致内存耗尽。所以,递归必须有一个终结条件。
2、回溯过程:回溯过程是递进过程的逆过程。函数调用的特点是, a 调用 b 后,b 结束一定要返回到 a。在递归调用过程中,当第 n 次调用完成后,会进入第 n-1 次,再进入 n-2 次……一直回到第一次调用。
函数就是一个逻辑块,递归过程也就是重复执行函数内的逻辑块的过程,所以递归可以实现循环语法的同等效应。理论上,循环语法实现的操作完全可以使用递归方式替换,但递归的性能消耗要远大于循环语法结构。
只有在使用循环语法结构不能实现或实现起来很麻烦的情况下才使用递归。
递归适合于解决,一个看起来很复杂的问题,其解决问题的关键点却在一个很的子问题上时。
如求一个数字的阶乘:计算 5!(5的阶乘)。
-
递进过程:5!=5X4! ,如果求出 4! 则 5!也就可求出,而 4!=4X3!,问题变成求 3!的阶乘,而 3!=3X2!,问题变成求 2!,而 2!=2X1!,问题变成求 1!,而 1! 就是 1。到此递进过程可以终止。
-
回溯过程:把 1! 的结果返回 2!,再把求得的 2!的结果返回求 3!,再把 3!的结果返回给求 4!,再把 4!的结果返回给 5!。最后得到结果。
def jc(num):
# 递归终止
if num == 1:
return 1
return num * jc(num - 1)
res = jc(5)
print(res)
如上面求某个数字阶乘的递归算法,属于线性递进,相对而言较容易理解。

再看一个例子:斐波拉契数列。
1,1,2,3,5,8,13,21……
从第三个数字开始,每一个数字都是前 2 个数字相加结果(第一,二位置的数字是 1)。此问题符合递归方案,如果想知道第 5 个位置的数字是匇,则需要知道第3,4个位置的数字是多少,如果要知道第3 个位置的则需要知道第1,2位置的数字是多少,如果要知道第 4 个位置的则要知道第 2,3位置的数字是多少。这个递进过程是一个树结构。
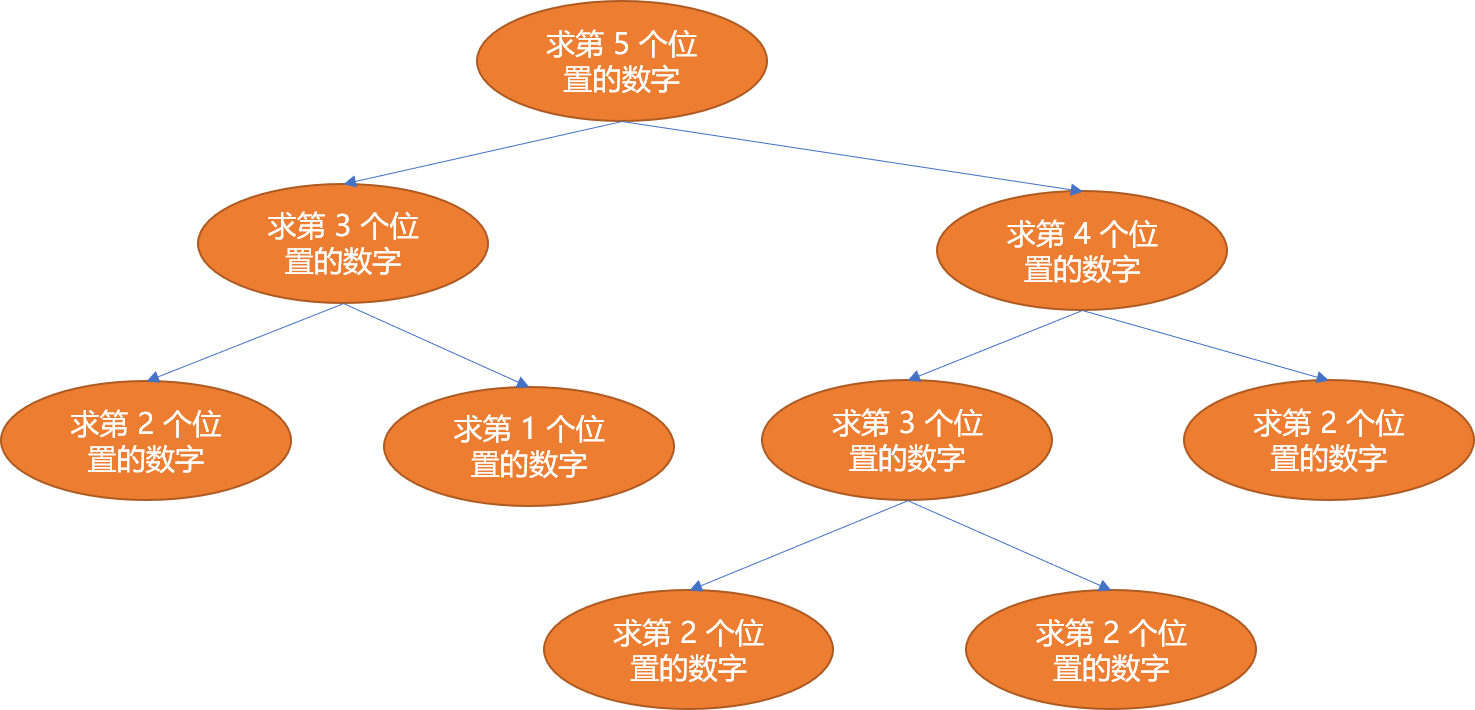
观察递进示意图,发现在求第 5 个位置数字时需要知道第 3 个位置数字,求第 4 位置数字也需要求解第 3 位置数字。第 3 个位置的数字求解在整个递进过程中至少计算了 2 次。
树结构的递进过程中,被重复计算是常见问题。一般会采用缓存机制,对于应该计算的数字就不再计算。
不使用缓存的常规递归算法:
def fb(pos):
if pos==1 or pos==2:
return 1
return fb(pos-1)+fb(pos-2)
res=fb(5)
print(res)
'''
输出结果
5
'''
使用缓存机制的算法:
#缓存器,位置作键,此位置的数字为值
cache = {}
def fb(pos):
if pos == 1 or pos == 2:
return 1
# 查看缓存中是否存在此位置已经计算出来的数字
if cache.get(pos) is not None:
return cache.get(pos)
# 缓存中没有,才递进
val = fb(pos - 2) + fb(pos - 1)
#得到值别忘记缓存
cache[pos] = val
return val
res = fb(5)
print(res)
'''
输出结果
5
'''
缓存机制的原理:需要某一个位置的数字时,先从缓存中查找,没有才继续递进。
再看一个例子:杨辉三角
杨辉三解的数字规律。每一行的第一列和最后一列为 1 ,每一行的其它列的值等于其左肩膀和右肩膀上的数字相加。
假设现在求第5行第3列的数字是多少?看如何使用递归方式计算。
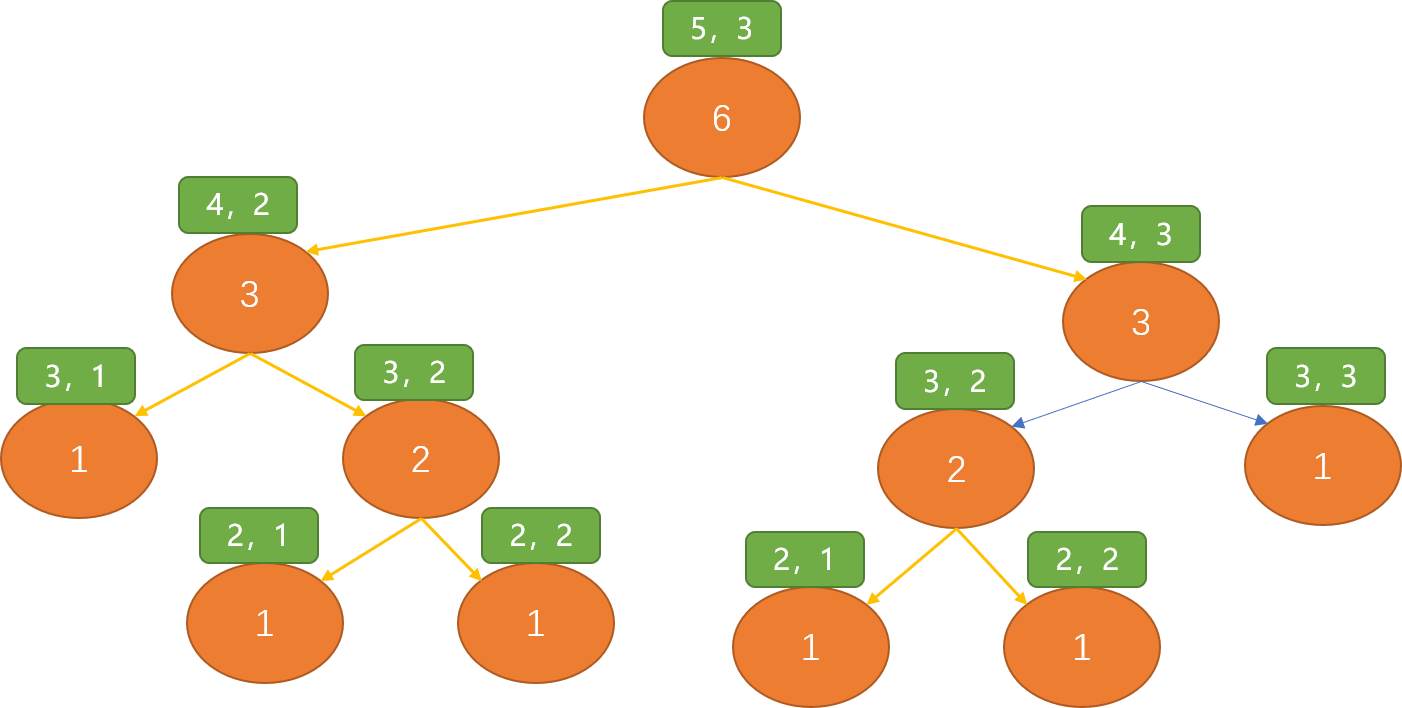
观察后,可看到(3,2)位置的数字被计算了两次,如果使用递归方式求解杨辉三解。当行数越多时,被重复计算的值就越多,性能消耗很严重。
为了提升性能,尽可能使用缓存机制。
常规不使用缓存机制:
import time
cache = {}
def yh(row, col):
if row == 1 or col == 1 or row == col:
return 1
return yh(row - 1, col - 1) + yh(row - 1, col - 2)
s = time.process_time()
res = yh(25, 5)
e = time.process_time()
print(res)
print('所使用的时间:',e - s)
'''
输出结果
5242885
所使用的时间: 1.671875
'''
使用缓存机制:
import time
def yh(row, col):
if row == 1 or col == 1 or row == col:
return 1
if cache.get((row, col)) is not None:
return cache.get((row, col))
val = yh(row - 1, col - 1) + yh(row - 1, col - 2)
cache[(row, col)] = val
return val
s = time.process_time()
res = yh(25, 5)
e = time.process_time()
print(res)
print("使用时间:",e - s)
'''
输出结果
5242885
使用时间: 0.0
'''
使用缓存和不使用缓存的运算时间差是很明显的。
4. 文件操作使用 open("文件路径","模式")。
模式有 r 可读,r+ 可读可写。当以 r 模式打开时,文件必须存在,
w 可写,w+ 可读可写,当以 w 模式打开时,文件可以不存在,如果存在,文件中内容会被清除。
a 可追加写,a+ 可追加写,可读。当以 a 模式打开时,文件可以不存在,如果存在,文件中内容不会被清除。
读方法:
with open("d:/temp.txt","r") as f :
# 读所有内容
f.read()
# 读一行
f.readline()
# 读出所有行
f.readlines()
写方法:
with open("d:/temp.txt","w") as f :
# 写入数据
f.write(1)
# 把列表数据写入
f.writelines([1,2])
# 使用 print 方法写入
print(123,34,sep=",",file=f)
对于 python 需要掌握的知识做了一个简单的归纳。
