中缀表达式转后缀表达式并计算结果

目录

• 1 栈的概念
• 2 何谓中缀表达式
• 3 后缀表达式(逆波兰)
  • 3.1 概念以及案例
  • 3.2 求解方法
    • 3.2.1 流程图
    • 3.2.2 推导相等优先级为何弹出栈顶
    • 3.2.3 案例
• 代码

1 栈的概念

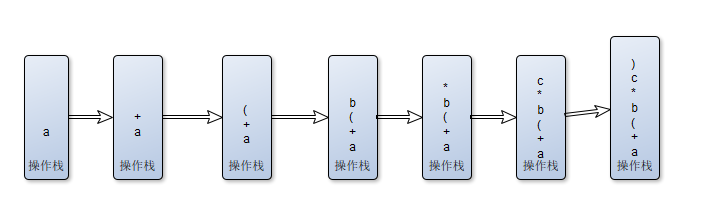
容器，先进后出规则；如图为表达式：a+(b*c) 逐个操作符、操作数入栈过程；出栈为该过程逆序

2 何谓中缀表达式

型如：a - b + c 的普通算术表达式，我们称之为中缀表达式。

3 后缀表达式(逆波兰) 3.1 概念以及案例

中缀表达式：a - b + c ，转化为后缀表达式：ab-c+；

后缀表达式运算规则：

1. 遇到操作数直接入栈，遇到操作符，从栈顶弹出两个操作数，并计算如下表达式结果压栈，直至最终弹出栈中最后一个数即停止算法，该记法的表达式称为后缀表达式

   后出栈操作数(两数中更靠近栈底者) （操作符[+_*/]） 先出栈操作数(栈顶)

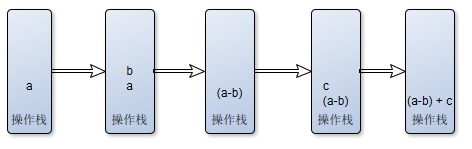
2. ab-c+计算过程如下图：

3.2 求解方法

入栈优先级

{ [ ( > 乘 = 除 > 加 = 减

3.2.1 流程图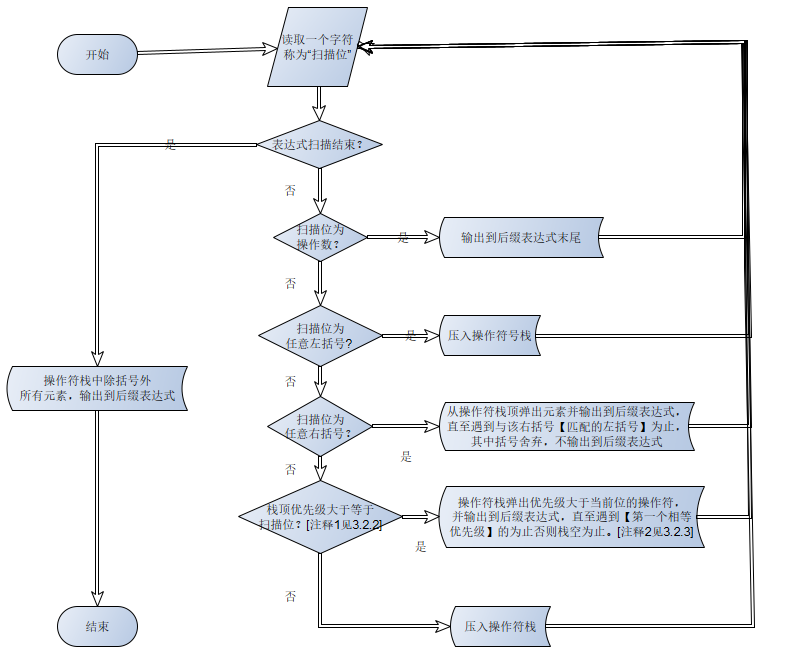

• 弹出案例：扫描位优先级较小，扫描位为 " - "。

• 左括号虽然优先级大，但是左括号只在碰到，匹配的右括号时弹出

3.2.2 推导相等优先级为何弹出栈顶

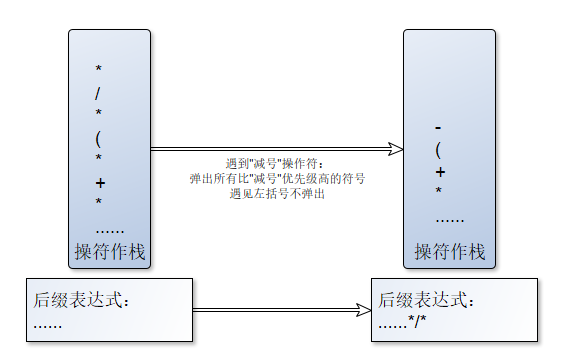
只关注相同有优先级下是否弹出栈顶

• 先加，后加减

中缀表达式 后缀表达式 a + b + c abc++ 或 ab+c+ a + b - c ab+c- 或 abc-+

此例中，当需要判断操作符间优先级：栈顶为：+(加)，栈外判断位：+ 或 - 。 此时若优先级相等，既可弹出栈顶操作符，也可不弹直接当前位压栈。

• 先减，后加减

中缀表达式 后缀表达式 a - b + c ab-c+ a - b - c ab-c-

此例中，当需要判断操作符间优先级：栈顶为：-(减)，栈外判断位：+ 或 - 。 此时若优先级相等，则只能弹出当前栈顶操作符。

• 先乘，后乘除

中缀表达式 后缀表达式 a * b * c abc** 或 abc a * b / c abc/ 或 abc/

此例中，当需要判断操作符间优先级：栈顶为：(乘)，栈外判断位： 或 / 。 此时若优先级相等，既可弹出栈顶操作符，也可不弹直接当前位压栈。

• 先除，后乘除

中缀表达式 后缀表达式 a / b * c ab/c* a / b / c ab/c/

此例中，当需要判断操作符间优先级：栈顶为：/(除)，栈外判断位： * 或 / 。 此时若优先级相等，则只能弹出当前栈顶操作符。

对比上述4种情景，取其交集，故在当前位等于栈顶优先级时，弹出栈顶。

3.2.3 案例

• 中缀表达式：2{1+2[4/(8-6)+7]}

下图为推推导过程，其中对部分直接入栈操作、或直接输出的操作进行了省略：

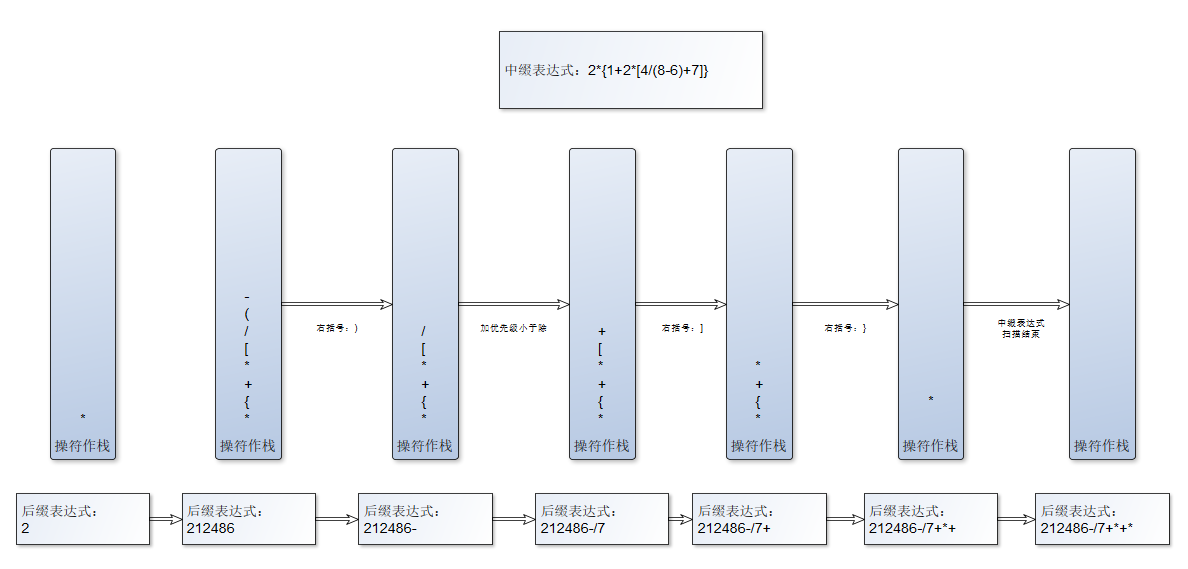
• 后缀表达式：2 1 2 4 8 6 - / 7 + * + *

代码

实际代码与推导过程略有差异，做了两个处理

1. 负数前加 0，例如 -5 * 3 转为 0 - 5 * 3

2. 读取连续数字，推导过程中使用的都是单个操作数，但是实际使用时肯定有多位数的操作，所以当读取到一个数字位时，则判断下一位是否为数字，读出连续数字。

import java.util.*;
import java.lang.*;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("\r\n输入一个合法中缀表达式：");
        while (scanner.hasNextLine()) {
            // 1.读取一行输入
            String nextLine = scanner.nextLine();
            List<String> express = new ArrayList<>();// 后缀表达式容器
            // 2.中缀转后缀
            handle(nextLine, express);
            System.out.print("后缀表达式：" + express);
            // 3.计算后缀表达式结果并输出
            execute(express);
            System.out.println("\r\n输入一个合法中缀表达式：");
        }
    }

    private static void handle(String nextLine, List<String> express) {
        Stack<Character> opt = new Stack<>();// 保存操作符
        int index = 0;
        while (index < nextLine.length()) {
            char c = nextLine.charAt(index);
            if (c == '-' && (index == 0 || getPower(nextLine.charAt(index -1)) == 10)) {// 含负数算式：-2*5, 转为: 0-2*5
                express.add(String.valueOf('0'));
            }
            if (c >= '0' && c <= '9') {// 一或多个连续数字
                StringBuilder tempSpace = new StringBuilder().append(c);
                while (index < nextLine.length() - 1 && (c = nextLine.charAt(index + 1)) >= '0' && c <= '9') {
                    tempSpace.append(c);
                    ++index;
                }
                express.add(tempSpace.toString());
                ++index;
            } else {
                if (opt.isEmpty()) {
                    opt.push(c);
                } else {
                    int power_c = getPower(c);
                    int power_top = getPower(opt.peek());
                    if (power_top == 10) {// 左括号
                        opt.push(c);
                    } else if (power_c == -10) {
                        while (!opt.isEmpty() && 10 != getPower(opt.peek())) {// 右括号，弹出所有操作符，直到遇到左括号为止
                            express.add(String.valueOf(opt.pop()));
                        }
                        if (!opt.isEmpty() && getPower(opt.peek()) == 10) opt.pop();// 弹出与之配对左括号
                    } else {// 四则运算符
                        if (power_top >= power_c) { // 栈顶优先级大于或等于当前位时， 弹出栈内元素直至遇到一个优先级相等的为止
                            while (!opt.isEmpty() && getPower(opt.peek()) < 10  && getPower(opt.peek()) >= power_c ) {
                                power_top = getPower(opt.peek());
                                express.add(String.valueOf(opt.pop()));
                                if (power_top == power_c) break;
                            }
                        }
                        opt.push(c);
                    }
                }
                ++index;
            }
        }
        while (!opt.isEmpty()) {
            if (getPower(opt.peek()) != 10 && getPower(opt.peek()) != -10)
                express.add(String.valueOf(opt.pop()));
        }
    }

    private static void execute(List<String> express) {
        int index = 0;
        Stack<Integer> temp = new Stack<>();
        while (index < express.size()) {
            String c = express.get(index);
            char currentOpt = c.charAt(0);
            if (c.length() > 1 ||  currentOpt >= '0' && currentOpt <= '9')
                temp.push(Integer.parseInt(c));
            else {
                int right = temp.pop();
                int left = temp.pop();
                if (currentOpt == '+') {
                    temp.push(left + right);
                } else if (currentOpt == '-') {
                    temp.push(left - right);
                } else if (currentOpt == '*') {
                    temp.push(left * right);
                } else if (currentOpt == '/') {
                    temp.push(left / right);
                }
            }
            ++index;
        }
        System.out.println("   计算结果：" + temp.pop());
    }

    public static int getPower(char c) {
        if (c == '{' || c == '[' || c == '(') {
            return 10;
        } else if (c == '*' || c == '/') {
            return 3;
        } else if (c == '+' || c == '-') {
            return 1;
        } else if (c == ')' || c == ']' || c == '}') {
            return -10;
        }
        return Integer.MIN_VALUE;
    }

}

• 部分测试用例：

    3*5+8-0*3-6+0+0
    5-3+9*6*(6-10-2)       # 连续数字
    3-10+(0+(10+5+3)-10)   # 连续数字
    3+2*{1+2*[-4/(8-6)+7]} # 含负数
    3+2*{1+2*[4/(8-6)+7]}
  

• 输出