- 设计思路
- 何为 LSM-Treee
- 参考资料
- 整体结构
- 内存表
- WAL
- SSTable 的结构
- SSTable 元素和索引的结构
- SSTable Tree
- 内存中的 SSTable
- 数据查找过程
- 实现过程
- Key/Value 的表示
- 内存表的实现
- 二叉排序树结构定义
- 插入操作
- 查找
- 删除
- 遍历算法
- WAL
- WAL 文件恢复过程
- SSTable 与 SSTable Tree
- SSTable 结构
- SSTable 文件结构
- SSTable Tree 结构和管理 SSTable 文件
- 插入 SSTable 文件过程
- 读取 SSTable 文件
- SSTable 文件合并
- SSTable 查找过程
- 简单的使用测试
- 文件压缩测试
- 插入测试
- 加载测试
- 查找测试
笔者前段时间在学习数据结构时,恰好听说了 LSM Tree,于是试着通过 LSM Tree 的设计思想,自己实现一个简单的 KV 数据库。
代码已开源,代码仓库地址:https://github.com/whuanle/lsm
笔者使用 Go 语言来实现 LSM Tree 数据库,因为 LSM Tree 的实现要求对文件进行读写、锁的处理、数据查找、文件压缩等,所以编码过程中也提高了对 Go 的使用经验,项目中也使用到了一些栈、二叉排序树等简单的算法,也可以巩固了基础算法能力。适当给自己设定挑战目标,可以提升自己的技术水平。
下面,我们来了解 LSM Tree 的设计思想以及如何实现一个 KV 数据库。
设计思路 何为 LSM-TreeeLSM Tree 的全称为Log-Structured Merge Tree,是一种关于键值类型数据库的数据结构。据笔者了解,目前 NoSQL 类型的数据库如 Cassandra 、ScyllaDB 等使用了 LSM Tree。
LSM Tree 的核心理论依据是磁盘顺序写性能比随机写的速度快很多。因为无论哪种数据库,磁盘 IO 都是对数据库读写性能的最大影响因素,因此合理组织数据库文件和充分利用磁盘读写文件的机制,可以提高数据库程序的性能。LSM Tree 首先会在内存中缓冲所有写操作,当使用的内存达到阈值时,便会将内存刷新磁盘中,这个过程只有顺序写,不会发生随机写,因此 LSM 具有优越的写入性能。
这里笔者就不对 LSM Tree 的概念进行赘述,读者可以参考下面列出的资料。
参考资料《What is a LSM Tree?》
https://dev.to/creativcoder/what-is-a-lsm-tree-3d75
生饼:《理解 LSM Tree:一种高效读写的存储引擎》
https://mp.weixin.qq.com/s/7kdg7VQMxa4TsYqPfF8Yug
肖汉松:《从0开始:500行代码实现 LSM 数据库》
https://mp.weixin.qq.com/s/kCpV0evSuISET7wGyB9Efg
小屋子大侠:《golang实践LSM相关内容》
https://blog.csdn.net/qq_33339479
《SM-based storage techniques: a survey》中文翻译
https://zhuanlan.zhihu.com/p/400293980
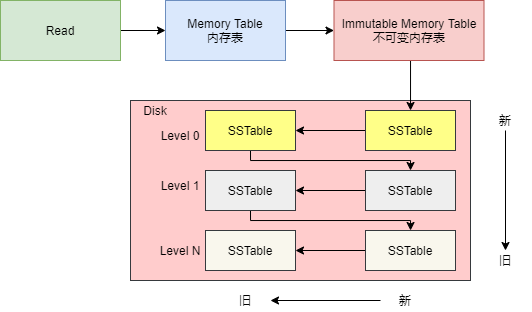
整体结构下图是 LSM Tree 的整体结构,整体可以分为内存、磁盘文件两大部分,其中磁盘文件除了数据库文件(SSTable 文件)外,还包括了 WAL 日志文件。
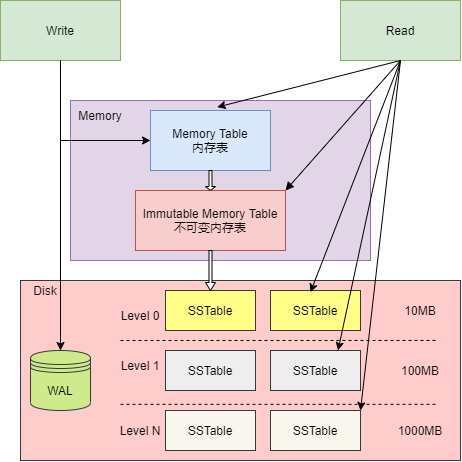
内存表用于缓冲写入操作,当 Key/Value 写入内存表后,也会同时记录到 WAL 文件中,WAL 文件可以作为恢复内存表数据的依据。程序启动时,如果发现目录中存在 WAL 文件,则需要读取 WAL 文件,恢复程序中的内存表。
在磁盘文件中,有着多层数据库文件, 每层都会存在多个 SSTable 文件,SSTable 文件用于存储数据,即数据库文件。下一层的数据库文件,都是上一层的数据库文件压缩合并后生成,因此,层数越大,数据库文件越大。
下面我们来了解详细一点的 LSM Tree 不同部分的设计思路,以及进行读写操作时,需要经过哪些阶段。
内存表在 LSM Tree 的内存区域中,有两个内存表,一个是可变内存表 Memory Table,一个是不可变内存表 Immutable Memory Table,两者具有相同的数据结构,一般是二叉排序树。
在刚开始时,数据库没有数据,此时 Memory Table 为空,即没有任何元素,而 Immutable Memory Table 为 nil,即没有被分配任何内存,此时,所有写操作均在 Memory Table 上,写操作包括设置 Key 的值和删除 Key。如果写入 Memory Table 成功,接着操作信息会记录到 WAL 日志文件中。
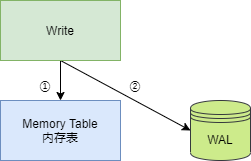
当然,Memory Table 中存储的 Key/Value 也不能太多,否则会占用太多内存,因此,一般当 Memory Table 中的 Key 数量达到阈值时,Memory Table 就会变成 Immutable Memory Table ,然后创建一个新的 Memory Table, Immutable Memory Table 会在合适的时机,转换为 SSTable,存储到磁盘文件中。
因此, Immutable Memory Table 是一个临时的对象,只在同步内存中的元素到 SSTable 时,临时存在。
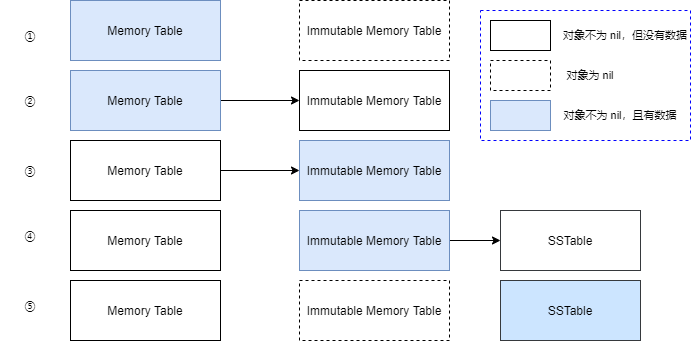
这里还要注意的是,当内存表被同步到 SSTable 后,Wal 文件是需要删除的。使用 Wal 文件可以恢复的数据应当与当前内存中的 KV 元素一致,即可以利用 WAL 文件恢复上一次程序的运行状态,如果当前内存表已经移动到 SSTable ,那么 WAL 文件已经没必要保留,应当删除并重新创建一个空的 WAL 文件。
WAL关于 WAL 部分的实现,有不同的做法,有的全局只有唯一一个 WAL 文件,有的则使用多个 WAL 文件,具体的实现会根据场景而变化。
WAL 即 Write Ahead LOG,当进行写入操作(插入、修改或删除 Key)时,因为数据都在内存中,为了避免程序崩溃停止或主机停机等,导致内存数据丢失,因此需要及时将写操作记录到 WAL 文件中,当下次启动程序时,程序可以从 WAL 文件中,读取操作记录,通过操作记录恢复到程序退出前的状态。
WAL 保存的日志,记录了当前内存表的所有操作,使用 WAL 恢复上一次程序的内存表时,需要从 WAL 文件中,读取每一次操作信息,重新作用于内存表,即重新执行各种写入操作。因此,直接对内存表进行写操作,和从 WAL 恢复数据重新对内存表进行写操作,都是一样的。
可以这样说, WAL 记录了操作过程,而且二叉排序树存储的是最终结果。
WAL 要做的是,能够还原所有对内存表的写操作,重新顺序执行这些操作,使得内存表恢复到上一次的状态。
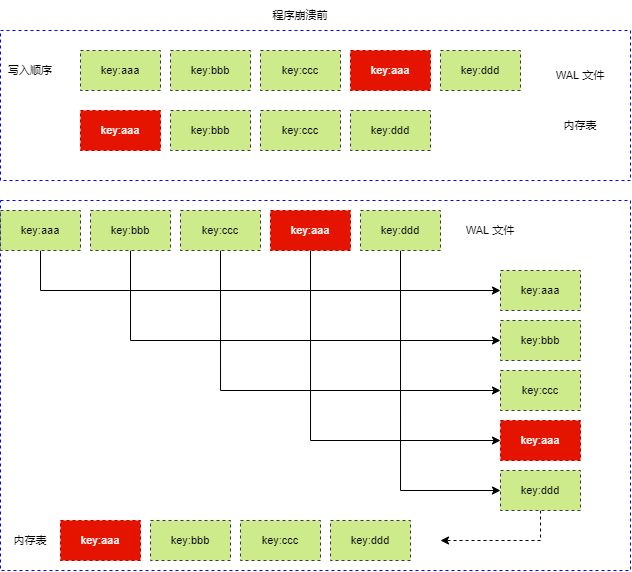
SSTable 的结构WAL 文件不是内存表的二进制文件备份,WAL 文件是对写操作的备份,还原的也是写操作过程,而不是内存数据。
SSTable 全称是 Sorted String Table,是内存表的持久化文件。
SSTable 文件由数据区、稀疏索引区、元数据三个部分组成,如下图所示。

内存表转换为 SSTable 时,首先遍历 Immutable Memory Table ,顺序将每个 KV 压缩成二进制数据,并且创建一个对应的索引结构,记录这个二进制 KV 的插入位置和数据长度。然后将所有二进制 KV 放到磁盘文件的开头,接着将所有的索引结构转为二进制,放在数据区之后。再将关于数据区和索引区的信息,放到一个元数据结构中,写入到文件末尾。
内存中每一个元素都会有一个 Key,在内存表转换为 SSTable 时,元素集合会根据 Key 进行排序,然后再将这些元素转换为二进制,存储到文件的开头,即数据区中。
但是,我们怎么从数据区中分隔出每一个元素呢?
对于不同的开发者,编码过程中,设置的 SSTable 的结构是不一样的,将内存表转为 SSTable 的处理方法也不一样,因此这里笔者只说自己在写 LSM Tree 时的做法。
笔者的做法是在生成数据区的时候,不将元素集合一次性生成二进制,而是一个个元素顺序遍历处理。
首先,将一个 Key/Value 元素,生成二进制,放到文件的开头,然后生成一个索引,记录这个元素二进制数据在文件的起始位置以及长度,然后将这个索引先放到内存中。
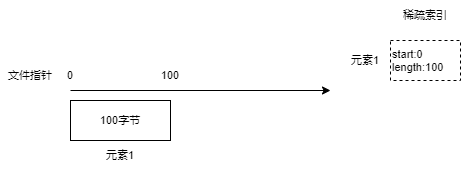
接着,不断处理剩下的元素,在内存中生成对应的索引。
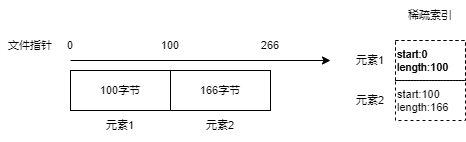
稀疏索引表示每一个索引执行文件中的一个数据块。
当所有元素处理完毕,此时 SSTable 文件已经生成数据区。接着,我们再将所有的索引集合,生成二进制数据,追加到文件中。
然后,我们还需要为数据区和稀疏索引区的起始位置和长度,生成文件元数据,以便后续读取文件时可以分割数据区和稀疏索引区,将两部分的数据单独处理。
元数据结构也很简单,其主要有四个值:
// 数据区起始索引
dataStart int64
// 数据区长度
dataLen int64
// 稀疏索引区起始索引
indexStart int64
// 稀疏索引区长度
indexLen int64
元数据会被追加到文件的末尾中,并且固定了字节长度。
在读取 SSTable 文件时,我们先读取文件最后的几个字节,如 64 个字节,然后根据每 8 个字节还原字段的值,生成元数据,然后就可以对数据区和稀疏索引区进行处理了。
SSTable 元素和索引的结构我们将一个 Key/Value 存储在数据区,那么这块存储了一个 Key/Value 元素的文件块,称为 block,为了表示 Key/Value,我们可以定义一个这样的结构:
Key
Value
Deleted
然后将这个结构转换为二进制数据,写到文件的数据区中。
为了定位 Key/Value 在数据区的位置,我们还需要定义一个索引,其结构如下:
Key
Start
Length
每个 Key/Value 使用一个索引进行定位。
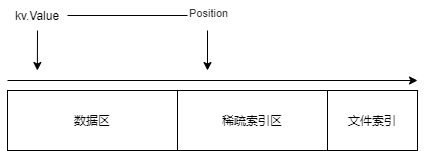
每次将内存表转换为 SSTable 时,都会生成一个 SSTable 文件,因此我们需要管理 SSTable 文件,以免文件数量过多。
下面是 LSM Tree 的 SSTable 文件组织结构。
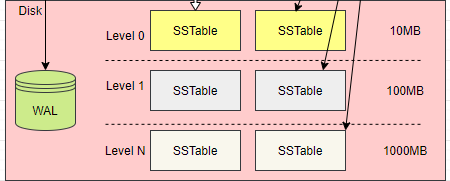
在上图中可以看到,数据库由很多的 SSTable 文件组成,而且 SSTable 被分隔在不同的层之中,为了管理不同层的 SSTable,所有 SSTable 磁盘文件的组织也有一个树结构,通过 SSTable Tree,管理不同层的磁盘文件大小或者 SSTable 数量。
关于 SSTable Tree,有三个要点:
1,第 0 层的 SSTable 文件,都是内存表转换的。
2,除第 0 层,下一层的 SSTable 文件,只能由上一层的 SSTable 文件通过压缩合并生成,而一层的 SSTable 文件在总文件大小或数量达到阈值时,才能进行合并,生成一个新的 SSTable 插入到下一层。
3,每一层的 SSTable 都有一个顺序,根据生成时间来排序。这个特点用于从所有的 SSTable 中查找数据。
由于每次持久化内存表,都会创建一个 SSTable 文件,因此 SSTable 文件数量会越来越多了,文件多了之后,需要保存较多的文件句柄,而且在多个文件中读取数据时,速度也会变慢。如果不进行控制,那么过多的文件会导致读性能变差以及占用空间过于膨胀,这一现象被称为空间放大和读放大。
由于 SSTable 是不能更改的,那么如果要删除一个 Key,或者修改一个 Key 的值,只能在新的 SSTable 中标记,而不能修改,这样会导致不同的 SSTable 存在相同的 Key,文件比较臃肿。
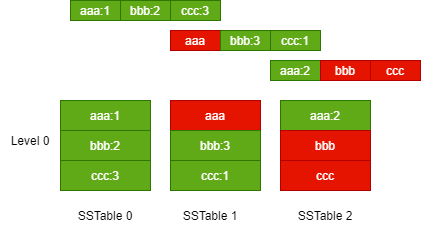
因此,还需要对小的 SSTable 文件进行压缩,合并成一个大的 SSTable 文件,放到下一层中,以便提高读取性能。
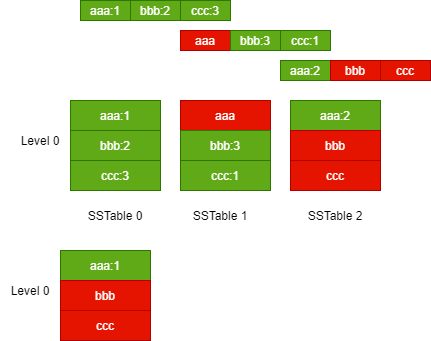
当一层的 SSTable 文件总大小大于阈值时,或者 SSTable 文件的数量太多时,就需要触发合并动作,生成新的 SSTable 文件,放入下一层中,再将原先的 SSTable 文件删除,下图演示了这一过程。
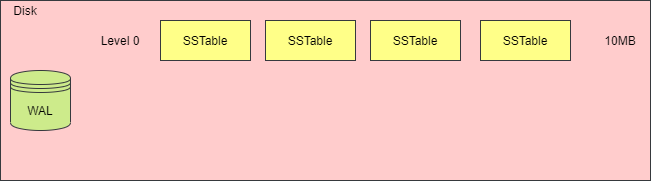
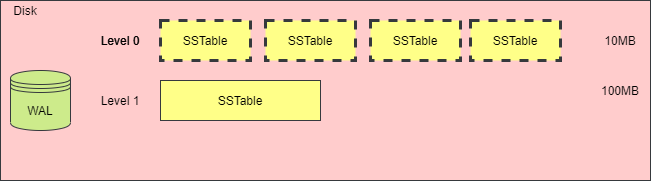
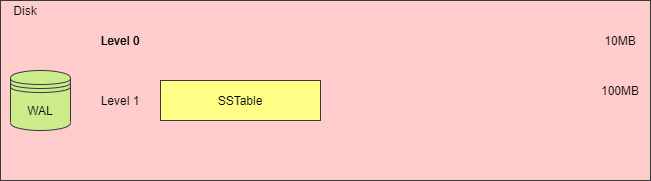
虽然对 SSTable 进行合并压缩,可以抑制空间放大和读放大问题,但是对多个 SSTable 合并为一个 SSTable 时,需要加载每个 SSTable 文件,在内存读取文件的内容,创建一个新的 SSTable 文件,并且删除掉旧的文件,这样会消耗大量的 CPU 时间和磁盘 IO。这种现象被称为写放大。
下图演示了合并前后的存储空间变化。
当程序启动后,会加载每个 SSTable 的元数据和稀疏索引区到内存中,也就是 SSTable 在内存中缓存了 Key 列表,需要在 SSTable 中查找 Key 时,首先在内存的稀疏索引区查找,如果找到 Key,则根据 索引的 Start 和 Length,从磁盘文件中读取 Key/Value 的二进制数据。接着将二进制数据转换为 Key/Value 结构。
因此,要确定一个 SSTable 是否存在某个 Key 时,是在内存中查找的,这个过程很快,只有当需要读取 Key 的值时,才需要从文件中读出。
可是,当 Key 数量太多时,全部缓存在内存中会消耗很多的内存,并且逐个查找也需要耗费一定的时间,还可以通过使用布隆过滤器(BloomFilter)来更快地判断一个 Key 是否存在。
数据查找过程首先根据要查找的 Key,从 Memory Table 中查询。
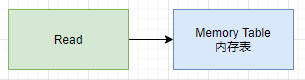
如果 Memory Table 中,找不到对应的 Key,则从 Immutable Memory Table 中查找。

笔者所写的 LSM Tree 数据库中,只有 Memory Table,没有 Immutable Memory Table。
如果在两个内存表中都查找不到 Key,那么就要从 SSTable 列表中查找。
首先查询第 0 层的 SSTable 表,从该层最新的 SSTable 表开始查找,如果没有找到,便查询同一层的其他 SSTable,如果还是没有,则接着查下一层。
当查找到 Key 时,无论 Key 状态如何(有效或已被删除),都会停止查找,返回此 Key 的值和删除标志。
实现过程在本节中,笔者将会说明自己实现 LSM Tree 大体的实现思路,从中给出一部分代码示例,但是完整的代码需要在仓库中查看,这里只给出实现相关的代码定义,不列出具体的代码细节。
下图是 LSM Tree 主要关注的对象:
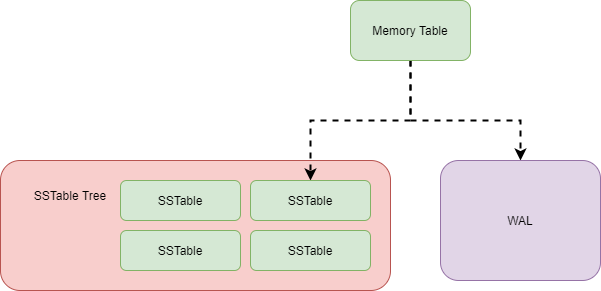
对于内存表,我们要实现增删查改、遍历;
对于 WAL,需要将操作信息写到文件中,并且能够从 WAL 文件恢复内存表;
对于 SSTable,能够加载文件信息,从中查找对应的数据;
对应 SSTable Tree,负责管理所有 SSTable,进行文件合并等。
Key/Value 的表示作为 Key/Value 数据库,我们需要能够保存任何类型的值。虽说 GO 1.18 增加了泛型,但是泛型结构体并不能任意存储任何值,解决存放各种类型的 Value 的问题,因此笔者不使用泛型结构体。而且,无论存储的是什么数据,对数据库来说是不重要,数据库也完全不必知道 Value 的含义,这个值的类型和含义,只对使用者有用,因此我们可以直接将值转为二进制存储,在用户取数据时,再将二进制转换为对应类型。
定义一个结构体,用于保存任何类型的值:
// Value 表示一个 KV
type Value struct {
Key string
Value []byte
Deleted bool
}
Value 结构体引用路径是 kv.Value。
如果有一个这样的结构体:
type TestValue struct {
A int64
B int64
C int64
D string
}
那么可以将结构体序列化后的二进制数据放到 Value 字段里。
data,_ := json.Marshal(value)
v := Value{
Key: "test",
Value: data,
Deleted: false,
}
Key/Value 通过 json 序列化值,转为二进制再存储到内存中。
因为在 LSM Tree 中,即使一个 Key 被删除了,也不会清理掉这个元素,只是将该元素标记为删除状态,所以为了确定查找结果,我们需要定义一个枚举,用于判断查找到此 Key 后,此 Key 是否有效。
// SearchResult 查找结果
type SearchResult int
const (
// None 没有查找到
None SearchResult = iota
// Deleted 已经被删除
Deleted
// Success 查找成功
Success
)
关于代码部分,读者可以参考:https://github.com/whuanle/lsm/blob/1.0/kv/Value.go
内存表的实现LSM Tree 中的内存表是一个二叉排序树,关于二叉排序树的操作,主要有设置值、插入、查找、遍历,详细的代码读者可以参考:
https://github.com/whuanle/lsm/blob/1.0/sortTree/SortTree.go
下面来简单说明二叉排序树的实现。
假设我们要插入的 Key 列表为 [30,45,25,23,17,24,26,28],那么插入后,内存表的结构如下所示:
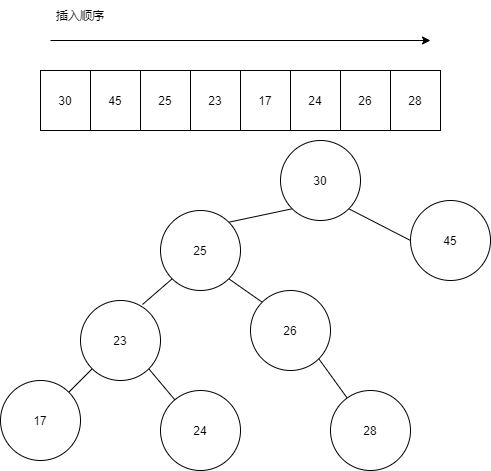
笔者在写二叉排序树时,发现几个容易出错的地方,因此这里列举一下。
首先,我们要记住:节点插入之后,位置不再变化,不能被移除,也不能被更换位置。
第一点,新插入的节点,只能作为叶子。
下面是一个正确的插入操作:
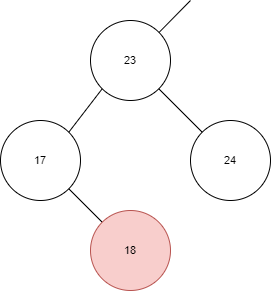
如图所示,本身已经存在了 23、17、24,那么插入 18 时,需要在 17 的右孩插入。
下面是一个错误的插入操作:
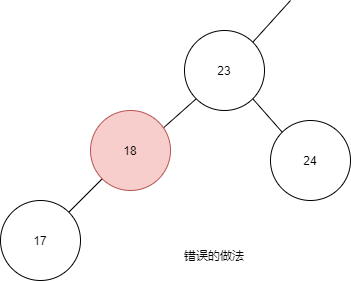
进行插入操作时,不能移动旧节点的位置,不能改变左孩右孩的关系。
第二点,删除节点时,只能标记删除,不能真正删除节点。
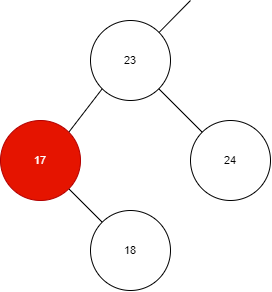
二叉排序树的结构体和方法定义如下:
// treeNode 有序树节点
type treeNode struct {
KV kv.Value
Left *treeNode
Right *treeNode
}
// Tree 有序树
type Tree struct {
root *treeNode
count int
rWLock *sync.RWMutex
}
// Search 查找 Key 的值
func (tree *Tree) Search(key string) (kv.Value, kv.SearchResult) {
}
// Set 设置 Key 的值并返回旧值
func (tree *Tree) Set(key string, value []byte) (oldValue kv.Value, hasOld bool) {
}
// Delete 删除 key 并返回旧值
func (tree *Tree) Delete(key string) (oldValue kv.Value, hasOld bool) {
}
具体的代码实现请参考:https://github.com/whuanle/lsm/blob/1.0/sortTree/SortTree.go
因为 Go 语言的 string 类型是值类型,因此能够直接比较大小的,因此在插入 Key/BValue 时,可以简化不少代码。
插入操作因为树是有序的,插入 Key/Value 时,需要在树的根节点从上到下对比 Key 的大小,然后以叶子节点的形式插入到树中。
插入过程,可以分为多种情况。
第一种,不存在相关的 Key 时,直接作为叶子节点插入,作为上一层元素的左孩或右孩。
if key < current.KV.Key {
// 左孩为空,直接插入左边
if current.Left == nil {
current.Left = newNode
// ... ...
}
// 继续对比下一层
current = current.Left
} else {
// 右孩为空,直接插入右边
if current.Right == nil {
current.Right = newNode
// ... ...
}
current = current.Right
}
第二种,当 Key 已经存在,该节点可能是有效的,我们需要替换 Value 即可;该节点有可能是被标准删除了,需要替换 Value ,并且将 Deleted 标记改成 false。
node.KV.Value = value
isDeleted := node.KV.Deleted
node.KV.Deleted = false
那么,当向二叉排序树插入一个 Key/Value 时,时间复杂度如何?
如果二叉排序树是比较平衡的,即左右比较对称,那么进行插入操作时,其时间复杂度为 O(logn)。
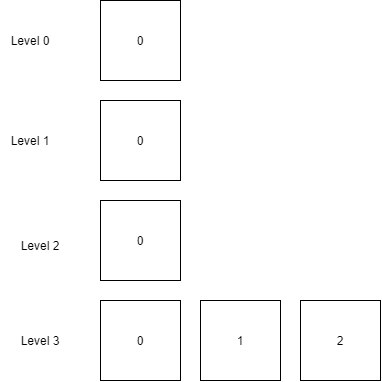
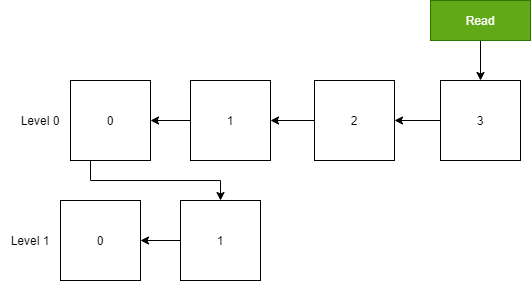
如下图所示,树中有 7 个节点,只有三层,那么插入操作时,最多需要对比三次。
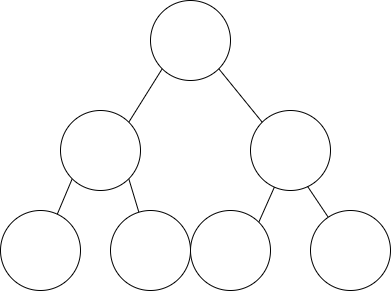
如果二叉排序树不平衡,最坏的情况是所有节点都在左边或右边,此时插入的时间复杂度为 O(n)。
如下图所示,树中有四个节点,也有四层,那么进行插入操作时,最多需要对比四次。
插入节点的代码请参考:https://github.com/whuanle/lsm/blob/5ea4f45925656131591fc9e1aa6c3678aca2a72b/sortTree/SortTree.go#L64
查找在二叉排序树中查找 Key 时,根据 Key 的大小来选择左孩或右孩进行下一层查找,查找代码示例如下:
currentNode := tree.root
// 有序查找
for currentNode != nil {
if key == currentNode.KV.Key {
if currentNode.KV.Deleted == false {
return currentNode.KV, kv.Success
} else {
return kv.Value{}, kv.Deleted
}
}
if key < currentNode.KV.Key {
// 继续对比下一层
currentNode = currentNode.Left
} else {
// 继续对比下一层
currentNode = currentNode.Right
}
}
其时间复杂度与插入一致。
查找代码请参考:https://github.com/whuanle/lsm/blob/5ea4f45925656131591fc9e1aa6c3678aca2a72b/sortTree/SortTree.go#L34
删除删除操作时,只需要查找到对应的节点,将 Value 清空,然后设置删除标记即可,该节点是不能被删除的。
currentNode.KV.Value = nil
currentNode.KV.Deleted = true
其时间复杂度与插入一致。
删除代码请参考:https://github.com/whuanle/lsm/blob/5ea4f45925656131591fc9e1aa6c3678aca2a72b/sortTree/SortTree.go#L125
遍历算法参考代码:https://github.com/whuanle/lsm/blob/5ea4f45925656131591fc9e1aa6c3678aca2a72b/sortTree/SortTree.go#L175
为了将二叉排序树的节点顺序遍历出来,递归算法是最简单的,但是当树的层次很高时,递归会导致消耗很多内存空间,因此我们需要使用栈算法,来对树进行遍历,顺序拿到所有节点。
Go 语言中,利用切片实现栈:https://github.com/whuanle/lsm/blob/1.0.0/sortTree/Stack.go
二叉排序树的顺序遍历,实际上就是前序遍历,按照前序遍历,遍历完成后,获得的节点集合,其 Key 一定是顺序的。
参考代码如下:
// 使用栈,而非递归,栈使用了切片,可以自动扩展大小,不必担心栈满
stack := InitStack(tree.count / 2)
values := make([]kv.Value, 0)
tree.rWLock.RLock()
defer tree.rWLock.RUnlock()
// 从小到大获取树的元素
currentNode := tree.root
for {
if currentNode != nil {
stack.Push(currentNode)
currentNode = currentNode.Left
} else {
popNode, success := stack.Pop()
if success == false {
break
}
values = append(values, popNode.KV)
currentNode = popNode.Right
}
}
遍历代码:https://github.com/whuanle/lsm/blob/33d61a058d79645c7b20fd41f500f2a47bc95357/sortTree/SortTree.go#L175

栈大小默认分配为树节点数量的一半,如果此树是平衡的,则数量大小比较合适。并且也不是将所有节点都推送到栈之后才能进行读取,只要没有左孩,即可从栈中取出元素读取。
如果树不是平衡的,那么实际需要的栈空间可能更大,但是这个栈使用了切片,如果栈空间不足,会自动扩展的。
遍历过程如下动图所示:
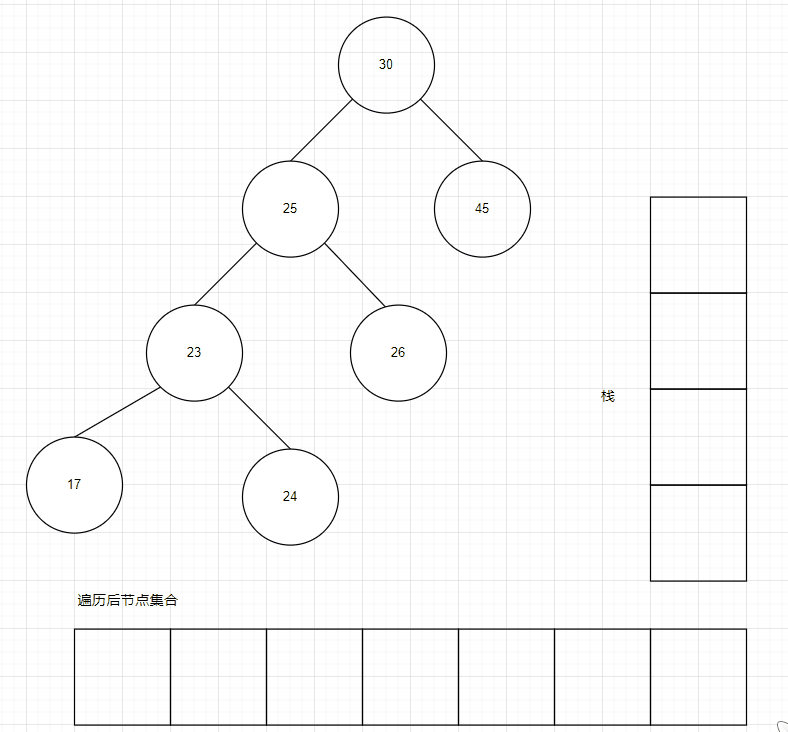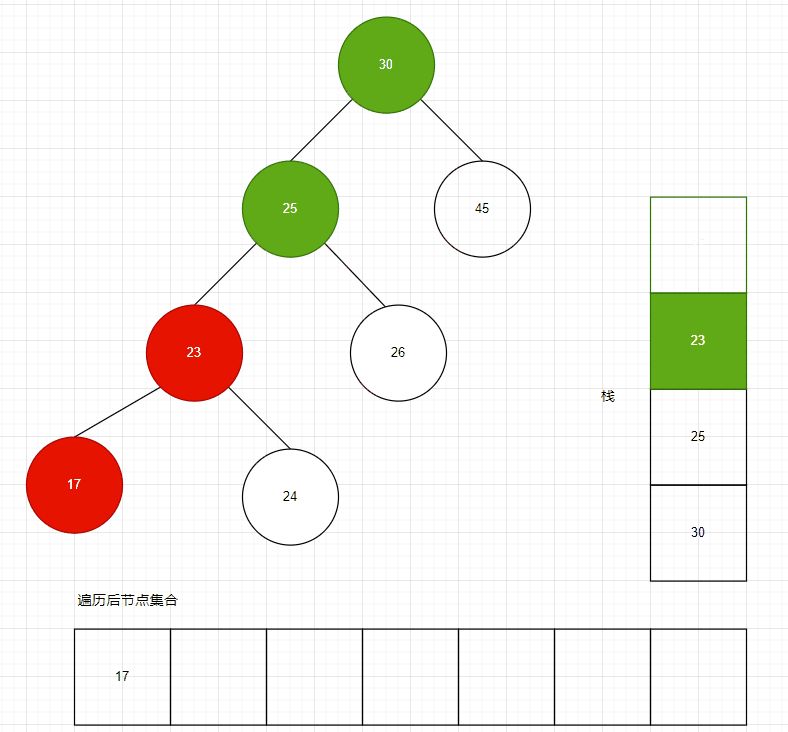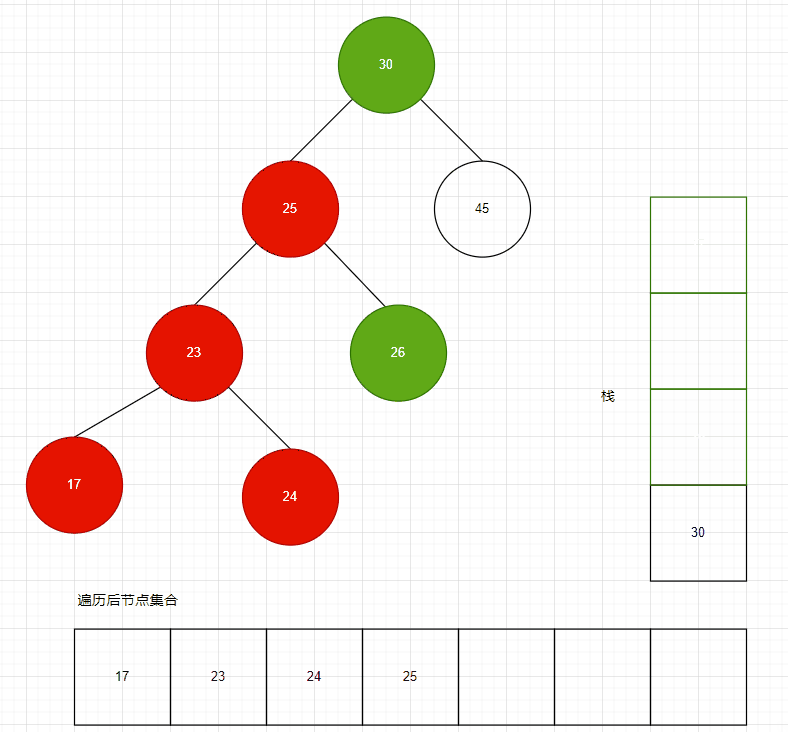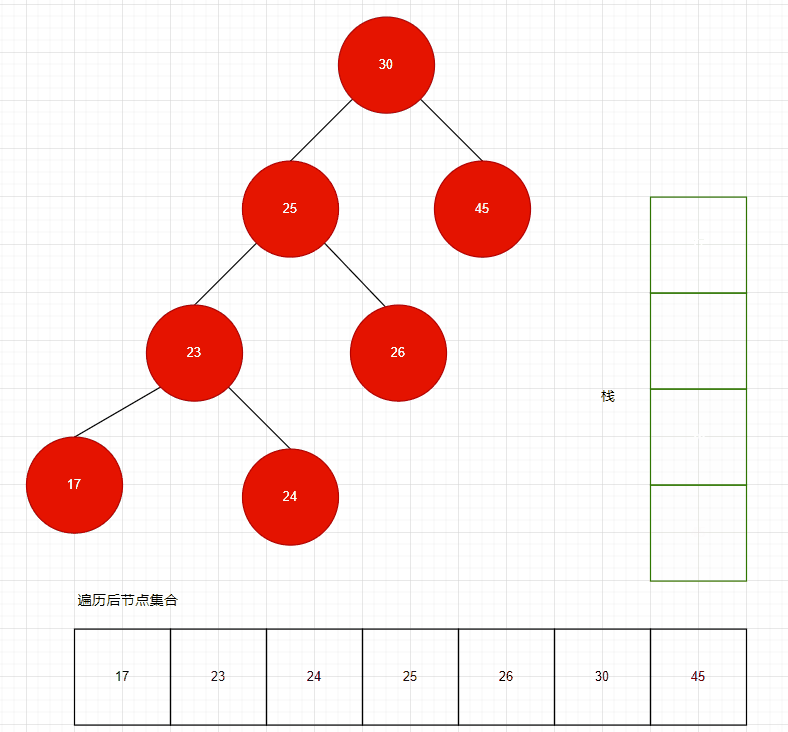
WAL动图制作不易~
可以看到,需要多少栈空间,与二叉树的高度有关。
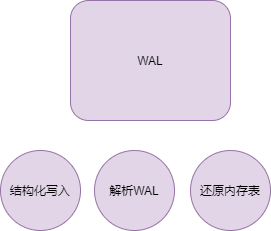
WAL 的结构体定义如下:
type Wal struct {
f *os.File
path string
lock sync.Locker
}
WAL 需要具备两种能力:
1,程序启动时,能够读取 WAL 文件的内容,恢复为内存表(二叉排序树)。
2,程序启动后,写入、删除操作内存表时,操作要写入到 WAL 文件中。
参考代码:https://github.com/whuanle/lsm/blob/1.0/wal/Wal.go
下面来讲解笔者的 WAL 实现过程。
下面是写入 WAL 文件的简化代码:
// 记录日志
func (w *Wal) Write(value kv.Value) {
data, _ := json.Marshal(value)
err := binary.Write(w.f, binary.LittleEndian, int64(len(data)))
err = binary.Write(w.f, binary.LittleEndian, data)
}
可以看到,先写入一个 8 字节,再将 Key/Value 序列化写入。
为了能够在程序启动时,正确从 WAL 文件恢复数据,那么必然需要对 WAL 文件做好正确的分隔,以便能够正确读取每一个元素操作。
因此,每一个被写入 WAL 的元素,都需要记录其长度,其长度使用 int64 类型表示,int64 占 8 个字节。

在上一小节中,写入 WAL 文件的一个元素,由元素数据及其长度组成。那么 WAL 的文件结构可以这样看待:

因此,在使用 WAL 文件恢复数据时,首先读取文件开头的 8 个字节,确定第一个元素的字节数量 n,然后将 8 ~ (8+n) 范围中的二进制数据加载到内存中,然后通过 json.Unmarshal() 将二进制数据反序列化为 kv.Value 类型。
接着,读取 (8+n) ~ (8+n)+8 位置的 8 个字节,以便确定下一个元素的数据长度,这样一点点把整个 WAL 文件读取完毕。
一般 WAL 文件不会很大,因此在程序启动时,数据恢复过程,可以将 WAL 文件全部加载到内存中,然后逐个读取和反序列化,识别操作是 Set 还是 Delete,然后调用二叉排序树的 Set 或 Deleted 方法,将元素都添加到节点中。
参考代码如下:
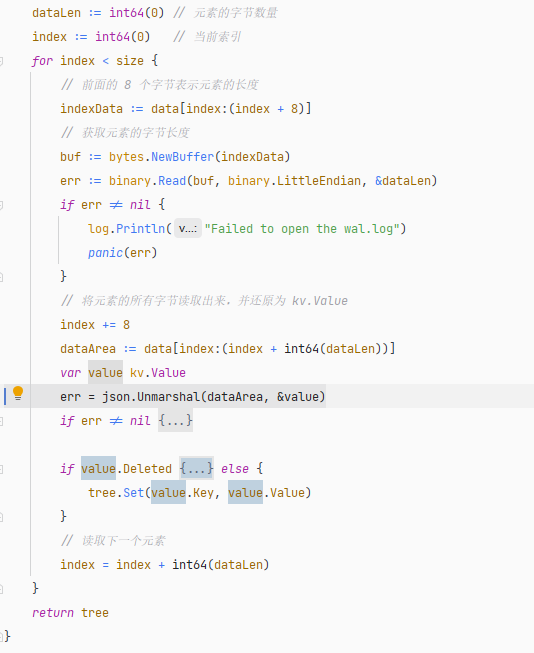
SSTable 与 SSTable Tree代码位置:https://github.com/whuanle/lsm/blob/4faddf84b63e2567118f0b34b5d570d1f9b7a18b/wal/Wal.go#L43
SSTable 涉及的代码比较多,可以根据保存 SSTable 文件 、 从文件解析 SSTable 和 搜索 Key 三部分进行划分。
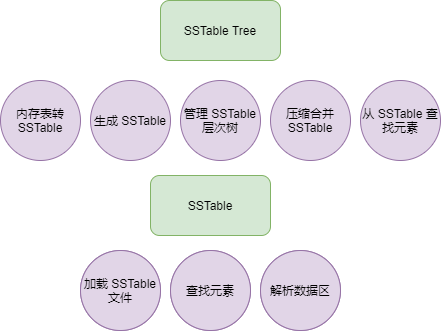
笔者所写的所有 SSTable 代码文件列表如下:

SSTable 的结构体定义如下:
// SSTable 表,存储在磁盘文件中
type SSTable struct {
// 文件句柄
f *os.File
filePath string
// 元数据
tableMetaInfo MetaInfo
// 文件的稀疏索引列表
sparseIndex map[string]Position
// 排序后的 key 列表
sortIndex []string
lock sync.Locker
}
sortIndex 中的元素是有序的,并且元素内存位置相连,便于 CPU 缓存,提高查找性能,还可以使用布隆过滤器,快速确定该 SSTable 中是否存在此 Key。
当确定该 SSTable 之后,便从 sparseIndex 中查找此元素的索引,从而可以在文件中定位。
其中元数据和稀疏索引的结构体定义如下:
type MetaInfo struct {
// 版本号
version int64
// 数据区起始索引
dataStart int64
// 数据区长度
dataLen int64
// 稀疏索引区起始索引
indexStart int64
// 稀疏索引区长度
indexLen int64
}
// Position 元素定位,存储在稀疏索引区中,表示一个元素的起始位置和长度
type Position struct {
// 起始索引
Start int64
// 长度
Len int64
// Key 已经被删除
Deleted bool
}
可以看到,一个 SSTable 结构体除了需要指向磁盘文件外,还需要在内存中缓存一些东西,不过不同开发者的做法不一样。就比如说笔者的做法,在一开始时,便固定了这种模式,需要在内存中缓存 Keys 列表,然后使用字典缓存元素定位。
// 文件的稀疏索引列表
sparseIndex map[string]Position
// 排序后的 key 列表
sortIndex []string
但实际上,只保留 sparseIndex map[string]Position也可以完成所有查找操作,sortIndex []string 不是必须的。
SSTable 的文件,分为数据区,稀疏索引区,元数据/文件索引,三个部分。存储的内容与开发者定义的数据结构有关。如下图所示:
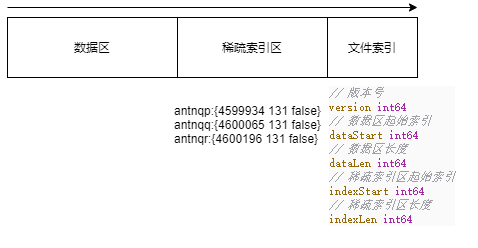
数据区是 序列化后的 Value 结构体列表,而稀疏索引区是序列化后的 Position 列表。不过两个区域的序列化处理方式不一样。
稀疏索引区,是 map[string]Position 类型序列化为二进制存储的,那么我们可以读取文件时,可以直接将稀疏索引区整个反序列化为 map[string]Position。
数据区,是一个个 kv.Value 序列化后追加的,因此是不能将整个数据区反序列化为 []kv.Value ,只能通过 Position 将数据区的每一个 block 逐步读取,然后反序列化为 kv.Value。
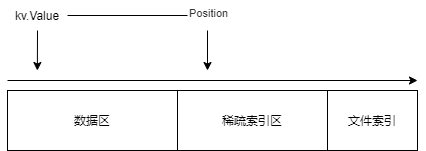
为了组织大量的 SSTable 文件,我们还需要一个结构体,以层次结构,去管理所有的磁盘文件。
我们需要定义一个 TableTree 结构体,其定义如下:
// TableTree 树
type TableTree struct {
levels []*tableNode // 这部分是一个链表数组
// 用于避免进行插入或压缩、删除 SSTable 时发生冲突
lock *sync.RWMutex
}
// 链表,表示每一层的 SSTable
type tableNode struct {
index int
table *SSTable
next *tableNode
}
为了方便对 SSTable 进行分层和标记插入顺序,需要制定 SSTable 文件的命名规定。
如下文件所示:
├── 0.0.db
├── 1.0.db
├── 2.0.db
├── 3.0.db
├── 3.1.db
├── 3.2.db
SSTable 文件由
{level}.{index}.db组成,第一个数字代表文件所在的 SSTable 层,第二个数字,表示在该层中的索引。其中,索引越大,表示其文件越新。
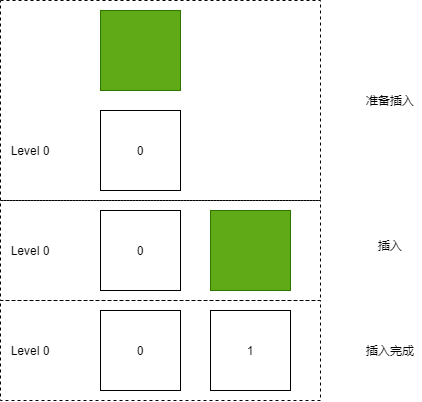
当从内存表转换为 SSTable 时,每个被转换的 SSTable ,都是插入到 Level 0 的最后面。
每一层的 SSTable 使用一个链表进行管理:
type tableNode struct {
index int
table *SSTable
next *tableNode
}
因此,在插入 SSTable 时,沿着往下查找,放到链表的最后面。
链表插入节点的代码部分示例如下:
for node != nil {
if node.next == nil {
newNode.index = node.index + 1
node.next = newNode
break
} else {
node = node.next
}
}
从内存表转换为 SSTable 时,会涉及比较多的操作,读者请参考代码:https://github.com/whuanle/lsm/blob/1.0/ssTable/createTable.go
读取 SSTable 文件当程序启动时,需要读取目录中所有的 SSTable 文件到 TableTree 中,接着加载每一个 SSTable 的稀疏索引区和元数据。
笔者的 LSM Tree 处理过程如图所示:
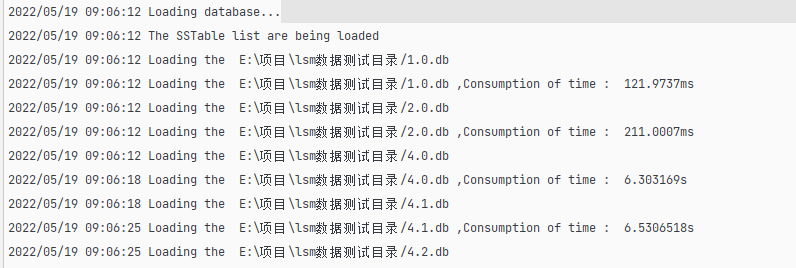
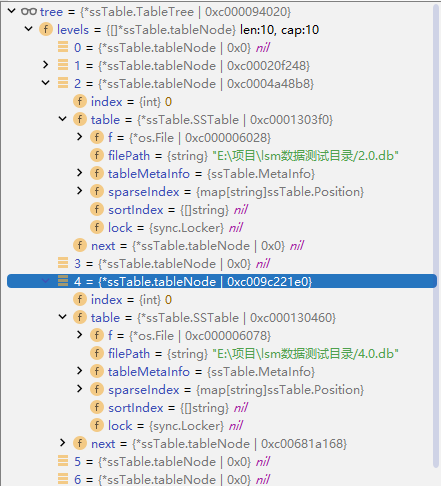
笔者的 LSM Tree 加载这些文件,一共耗时 19.4259983s 。
加载过程的代码在:https://github.com/whuanle/lsm/blob/1.0/ssTable/Init.go
下面笔者说一下大概的加载过程。
首先读取目录中的所有 .db 文件:
infos, err := ioutil.ReadDir(dir)
if err != nil {
log.Println("Failed to read the database file")
panic(err)
}
for _, info := range infos {
// 如果是 SSTable 文件
if path.Ext(info.Name()) == ".db" {
tree.loadDbFile(path.Join(dir, info.Name()))
}
}
然后创建一个 SSTable 对象,加载文件的元数据和稀疏索引区:
// 加载文件句柄的同时,加载表的元数据
table.loadMetaInfo()
// 加载稀疏索引区
table.loadSparseIndex()
最后根据 .db 的文件名称,插入到 TableTree 中指定的位置:
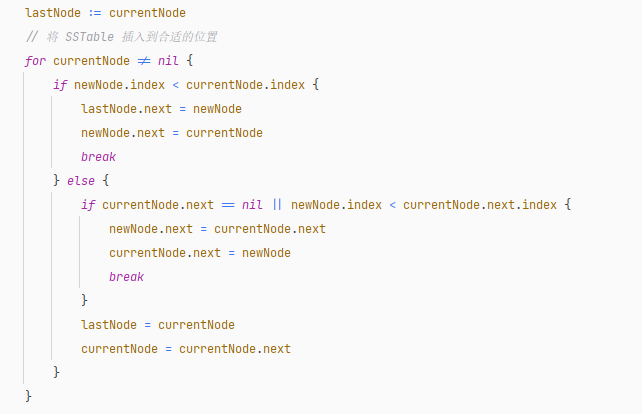
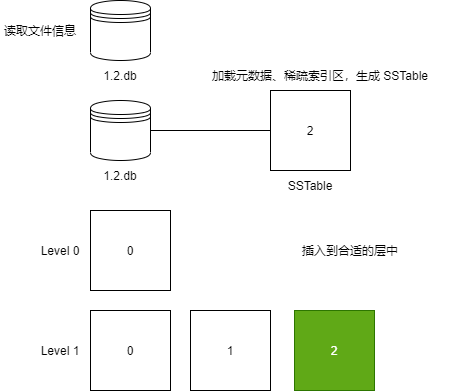
当一层的 SSTable 文件太多时,或者文件太大时,需要将该层的 SSTable 文件,合并起来,生成一个新的、没有重复元素的 SSTable,放到新的一层中。
因此,笔者的做法是在程序启动后,使用一个新的线程,检查内存表是否需要被转换为 SSTable、是否需要压缩 SSTable 层。检查时, 从 Level 0 开始,检查两个条件阈值,第一个是 SSTable 数量,另一个是该层 SSTable 的文件总大小。
SSTable 文件合并阈值,在程序启动的时候,需要设置。
lsm.Start(config.Config{
DataDir: `E:\项目\lsm数据测试目录`,
Level0Size: 1, // 第0层所有 SSTable 文件大小之和的阈值
PartSize: 4, // 每一层 SSTable 数量阈值
Threshold: 500, // 内存表元素阈值
CheckInterval: 3, // 压缩时间间隔
})
每一层的 SSTable 文件大小之和,是根据第 0 层生成的,例如,当你设置第 0 层为 1MB 时,第 1 层则为 10MB,第 2 层则为 100 MB,使用者只需要设置第 0 层的文件总大小阈值即可。
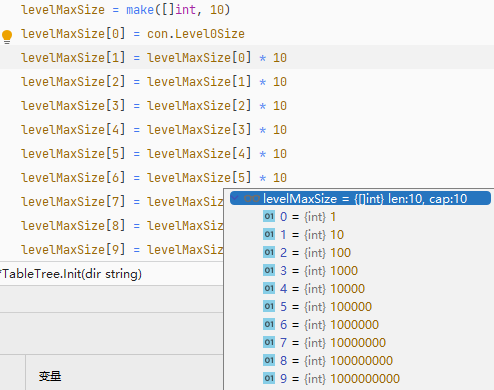
下面来说明 SSTable 文件合并过程。
压缩合并的完整代码请参考:https://github.com/whuanle/lsm/blob/1.0/ssTable/compaction.go
下面是初始的文件树:
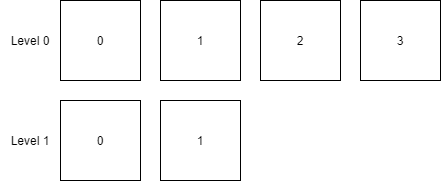
首先创建一个二叉排序树对象:
memoryTree := &sortTree.Tree{}
然后在 Level 0 中,从索引最小的 SSTable 开始,读取文件数据区中的每一个 block,反序列化后,进行插入操作或删除操作。
for k, position := range table.sparseIndex {
if position.Deleted == false {
value, err := kv.Decode(newSlice[position.Start:(position.Start + position.Len)])
if err != nil {
log.Fatal(err)
}
memoryTree.Set(k, value.Value)
} else {
memoryTree.Delete(k)
}
}
将 Level 0 的所有 SSTable 加载到二叉排序树中,即合并所有元素。
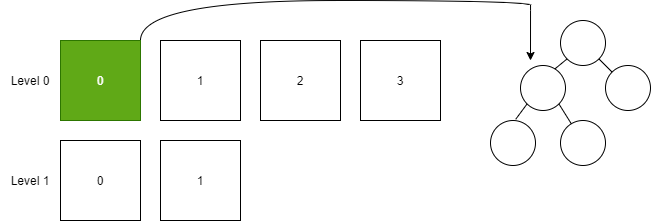
然后将二叉排序树转换为 SSTable,插入到 Level 1 中。
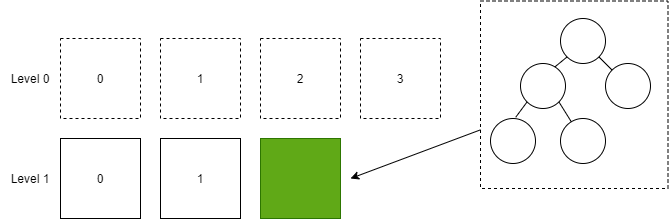
接着,删除 Level 0 的所有 SSTable 文件。
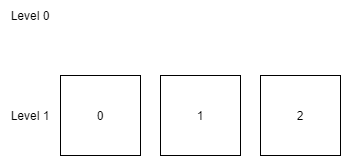
注,由于笔者的压缩方式会将文件加载到内存中,使用切片存储文件数据,因此可能会出现容量过大的错误。

SSTable 查找过程这是一个值得关注的地方。
完整的代码请参考:https://github.com/whuanle/lsm/blob/1.0/ssTable/Search.go
当需要查找一个元素时,首先在内存表中查找,查找不到时,需要在 TableTree 中,逐个查找 SSTable。
// 遍历每一层的 SSTable
for _, node := range tree.levels {
// 整理 SSTable 列表
tables := make([]*SSTable, 0)
for node != nil {
tables = append(tables, node.table)
node = node.next
}
// 查找的时候要从最后一个 SSTable 开始查找
for i := len(tables) - 1; i >= 0; i-- {
value, searchResult := tables[i].Search(key)
// 未找到,则查找下一个 SSTable 表
if searchResult == kv.None {
continue
} else { // 如果找到或已被删除,则返回结果
return value, searchResult
}
}
}
在 SSTable 内部查找时,使用了二分查找法:
// 元素定位
var position Position = Position{
Start: -1,
}
l := 0
r := len(table.sortIndex) - 1
// 二分查找法,查找 key 是否存在
for l <= r {
mid := int((l + r) / 2)
if table.sortIndex[mid] == key {
// 获取元素定位
position = table.sparseIndex[key]
// 如果元素已被删除,则返回
if position.Deleted {
return kv.Value{}, kv.Deleted
}
break
} else if table.sortIndex[mid] < key {
l = mid + 1
} else if table.sortIndex[mid] > key {
r = mid - 1
}
}
if position.Start == -1 {
return kv.Value{}, kv.None
}
关于 LSM Tree 数据库的编写,就到这里完毕了,下面了解笔者的数据库性能和使用方法。
简单的使用测试示例代码位置:https://gist.github.com/whuanle/1068595f46824466227b93ef583499d3
首先下载依赖包:
go get -u github.com/whuanle/lsm@v1.0.0
然后使用 lsm.Start() 初始化数据库,再增删查改 Key,示例代码如下:
package main
import (
"fmt"
"github.com/whuanle/lsm"
"github.com/whuanle/lsm/config"
)
type TestValue struct {
A int64
B int64
C int64
D string
}
func main() {
lsm.Start(config.Config{
DataDir: `E:\项目\lsm数据测试目录`,
Level0Size: 1,
PartSize: 4,
Threshold: 500,
CheckInterval: 3, // 压缩时间间隔
})
// 64 个字节
testV := TestValue{
A: 1,
B: 1,
C: 3,
D: "00000000000000000000000000000000000000",
}
lsm.Set("aaa", testV)
value, success := lsm.Get[TestValue]("aaa")
if success {
fmt.Println(value)
}
lsm.Delete("aaa")
}
文件压缩测试testV 是 64 字节,而 kv.Value 保存了 testV 的值,kv.Value 字节大小为 131。
我们可以写一个从 26 个字母中取任意 6 字母组成 Key,插入到数据库中,从中观察文件压缩合并,和插入速度等。

不同循环层次插入的元素数量:
生成的测试文件列表:

文件压缩合并动图过程的如下(约20秒):

下面是一些不严谨的测试结果。
设置启动数据库时的配置:
lsm.Start(config.Config{
DataDir: `E:\项目\lsm数据测试目录`,
Level0Size: 10, // 0 层 SSTable 文件大小
PartSize: 4, // 每层文件数量
Threshold: 3000, // 内存表阈值
CheckInterval: 3, // 压缩时间间隔
})
lsm.Start(config.Config{
DataDir: `E:\项目\lsm数据测试目录`,
Level0Size: 100,
PartSize: 4,
Threshold: 20000,
CheckInterval: 3,
})
插入数据:
func insert() {
// 64 个字节
testV := TestValue{
A: 1,
B: 1,
C: 3,
D: "00000000000000000000000000000000000000",
}
count := 0
start := time.Now()
key := []byte{'a', 'a', 'a', 'a', 'a', 'a'}
lsm.Set(string(key), testV)
for a := 0; a < 1; a++ {
for b := 0; b < 1; b++ {
for c := 0; c < 26; c++ {
for d := 0; d < 26; d++ {
for e := 0; e < 26; e++ {
for f := 0; f < 26; f++ {
key[0] = 'a' + byte(a)
key[1] = 'a' + byte(b)
key[2] = 'a' + byte(c)
key[3] = 'a' + byte(d)
key[4] = 'a' + byte(e)
key[5] = 'a' + byte(f)
lsm.Set(string(key), testV)
count++
}
}
}
}
}
}
elapse := time.Since(start)
fmt.Println("插入完成,数据量:", count, ",消耗时间:", elapse)
}
两次测试,生成的 SSTable 总文件大小都是约 82MB。
两次测试消耗的时间:
插入完成,数据量: 456976 ,消耗时间: 1m43.4541747s
插入完成,数据量: 456976 ,消耗时间: 1m42.7098146s
因此,每个元素 131 个字节,这个数据库 100s 可以插入 约 45w 条数据,即每秒插入 4500 条数据。
如果将 kv.Value 的值比较大,测试在 3231 字节时,插入 456976 条数据,文件约 1.5GB,消耗时间 2m10.8385817s,即每秒插入 3500条。
插入较大值的 kv.Value,代码示例:https://gist.github.com/whuanle/77e756801bbeb27b664d94df8384b2f9
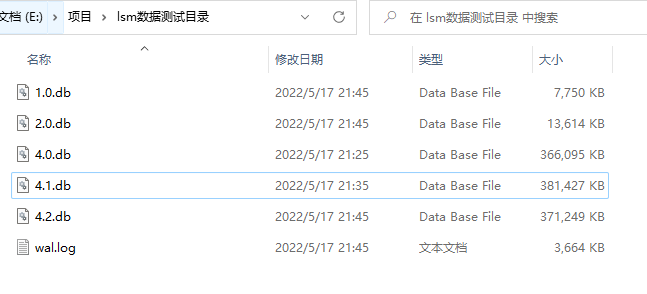
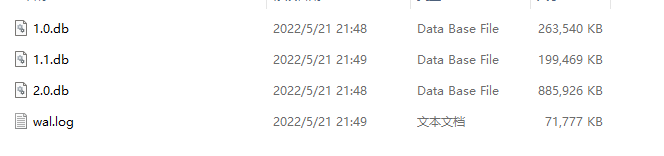
加载测试下面是每个元素 3231 字节时,插入 45 万条数据后的 SSTable 文件列表,程序启动时,我们需要加载这些文件。
2022/05/21 21:59:30 Loading wal.log...
2022/05/21 21:59:32 Loaded wal.log,Consumption of time : 1.8237905s
2022/05/21 21:59:32 Loading database...
2022/05/21 21:59:32 The SSTable list are being loaded
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/1.0.db
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/1.0.db ,Consumption of time : 92.9994ms
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/1.1.db
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/1.1.db ,Consumption of time : 65.9812ms
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/2.0.db
2022/05/21 21:59:32 Loading the E:\项目\lsm数据测试目录/2.0.db ,Consumption of time : 331.6327ms
2022/05/21 21:59:32 The SSTable list are being loaded,consumption of time : 490.6133ms
可以看到,除 WAL 加载比较耗时(因为要逐个插入内存中),SSTable 文件的加载还是比较快的。
查找测试如果元素都在内存中时,即使有 45 万条数据,查找速度也是非常快的,例如查找 aaaaaa(Key最小)和 aazzzz(Key最大)的数据,耗时都很低。
下面使用每条元素 3kb 的数据库文件进行测试。
查找代码:
start := time.Now()
elapse := time.Since(start)
v, _ := lsm.Get[TestValue]("aaaaaa") // 或者 aazzzz
fmt.Println("查找完成,消耗时间:", elapse)
fmt.Println(v)
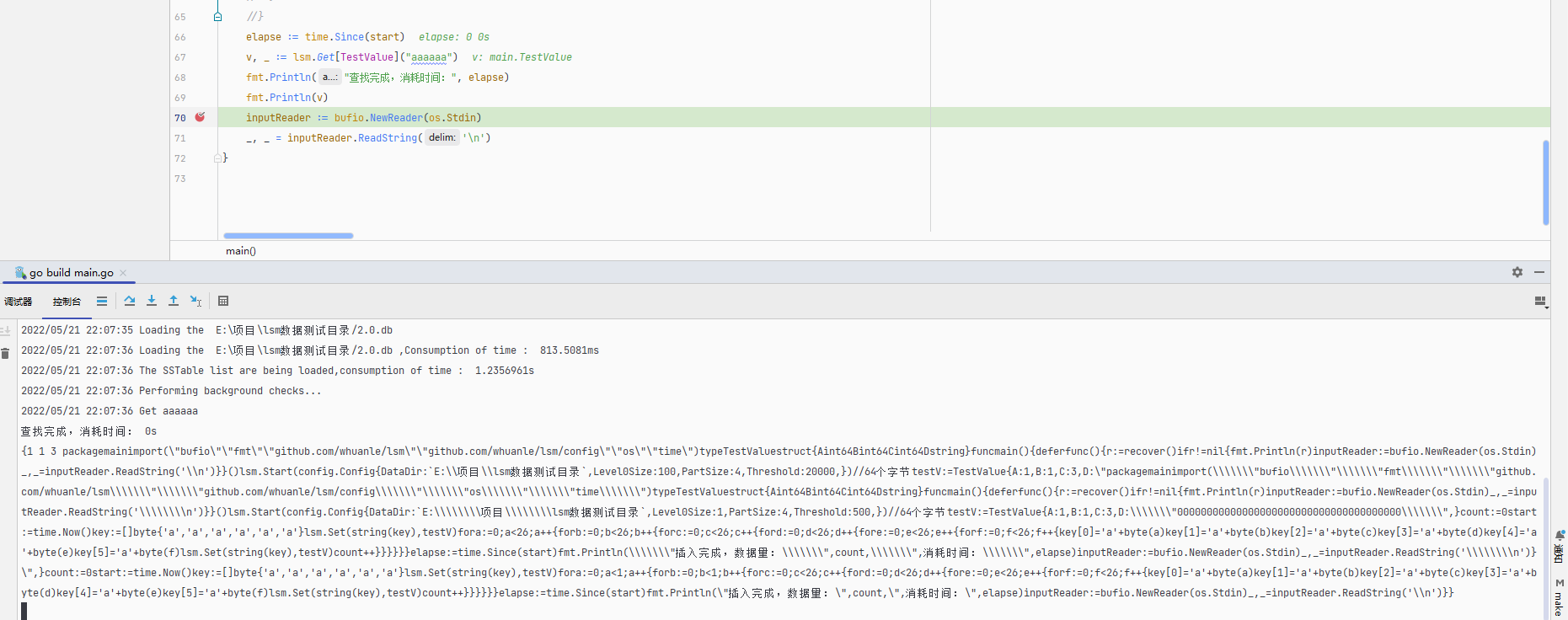
如果在 SSTable 中查找,因为 aaaaaa 是首先被写入的,因此必定会在最底层的 SSTable 文件的末尾,需要消耗的时间比较多。
SSTable 文件列表:
├── 1.0.db 116MB
├── 2.0.db 643MB
├── 2.1.db 707MB
约 1.5GB
aaaaaa 在 2.0db 中,查找时会以 1.0.db、2.1.db、2.0.db 的顺序加载。
查询速度测试:
2022/05/22 08:25:43 Get aaaaaa
查找 aaaaaa 完成,消耗时间: 19.4338ms
2022/05/22 08:25:43 Get aazzzz
查找 aazzzz 完成,消耗时间: 0s

关于笔者的 LSM Tree 数据库,就介绍到这里,详细的实现代码,请参考 Github 仓库。
一个逗逗的大学生

