MSDN对它的说明是:对序列应用累加器函数。备注中还有一些说明,大意是这个方法比较复杂,一般情况下用Sum、Max、Min、Average就可以了。
看看下面的代码,有了Sum,谁还会用Aggregate呢!
public static void Test1()
{
int[] nums = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int sum1 = nums.Sum();
int sum2 = nums.Aggregate((i,j)=>i+j);
}同是求和,Sum不再需要额外参数,而Aggregate确还要将一个lambda作为参数。因为用起来麻烦,操作太低级,Aggregate渐渐被大多人忽视了...
实际上Aggregate因为“低级”,功能确是很强大的,通过它可以简化很多聚合运算。
首先来看对Aggregate组装字符串的问题:
public static void Test2()
{
string[] words = new string[] { "Able", "was", "I", "ere", "I", "saw", "Elba"};
string s = words.Aggregate((a, n) => a + " " + n);
Console.WriteLine(s);
}
输出结果是:Able was I ere I saw Elba (注:出自《大国崛起》,狄娜最后讲述了拿破仑一句经典)。
当然考虑性能的话还是用StringBuilder吧,这里主要介绍用法。这个Sum做不到吧!
Aggregate还可以将所有字符串倒序累加,配合String.Reverse扩展可以实现整个句子的倒序输出:
 public static void Test3()
public static void Test3() {
{ string[] words = new string[] { "Able", "was", "I", "ere", "I", "saw", "Elba"};
string[] words = new string[] { "Able", "was", "I", "ere", "I", "saw", "Elba"}; string normal = words.Aggregate((a, n) => a + " " + n);
string normal = words.Aggregate((a, n) => a + " " + n); string reverse = words.Aggregate((a, n) => n.Reverse() + " " + a);
string reverse = words.Aggregate((a, n) => n.Reverse() + " " + a);
 Console.WriteLine("正常:" + normal);
Console.WriteLine("正常:" + normal); Console.WriteLine("倒置:" + reverse);
Console.WriteLine("倒置:" + reverse); }
} // 倒置字符串,输入"abcd123",返回"321dcba"
// 倒置字符串,输入"abcd123",返回"321dcba" public static string Reverse(this string value)
public static string Reverse(this string value) {
{ char[] input = value.ToCharArray();
char[] input = value.ToCharArray(); char[] output = new char[value.Length];
char[] output = new char[value.Length];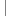 for (int i = 0; i < input.Length; i++)
for (int i = 0; i < input.Length; i++)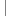 output[input.Length - 1 - i] = input[i];
output[input.Length - 1 - i] = input[i];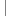 return new string(output);
return new string(output);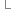 }
}
看下面,输出结果好像不太对:
怎么中间的都一样,两的单词首尾字母大小写发生转换了呢?!
仔细看看吧,不是算法有问题,是输入“有问题”。搜索一下“Able was I ere I saw Elba”,这可是很有名的英文句子噢!
Aggregate还可以实现异或(^)操作:
{
byte[] data = new byte[] { 0x31, 0x32, 0x33, 0x34, 0x35 };
byte checkSum = data.Aggregate((a, n) => (byte)(a ^ n));
}
对经常作串口通信的朋友比较实用。
看来Aggregate也是比较“简单易用”的,深入一步来看看它是怎么实现的吧,使用Reflector,反编译一下System.Core.dll。
以下代码取自反编译结果,为了演示删除了其中的空值判断代码:
也很简单吧,就是一个循环!前面lambda表达式中参数a, n 分别对应current, enumerator.Current,对照一下,还是很好理解的。
现在我们想求整数数组中位置为偶数的数的和(间隔求和),可以用Where配合Sum:
{
int[] nums = new int[] { 10, 20, 30, 40, 50 };
int sum1 = nums.Where((n, i) => i % 2 == 0).Sum();//10 + 30 + 50
}
这个Where扩展设计的很好,它不但能带出某项的值“n”,还能带出项的位置“i”。
Aggregate可不行!我们来改进一下:
public static TSource Aggregate<TSource>(this IEnumerable<TSource> source, Func<TSource, TSource, int, TSource> func)
{
int index = 0;
using (IEnumerator<TSource> enumerator = source.GetEnumerator())
{
enumerator.MoveNext();
index++;
TSource current = enumerator.Current;
while (enumerator.MoveNext())
current = func(current, enumerator.Current, index++);
return current;
}
}
改进后的Aggregate更加强大,前面的求偶数位置数和的算法可以写成下面的样子:
public static void Test6(){
int[] nums = new int[] { 10, 20, 30, 40, 50 };
int sum2 = nums.Aggregate((a, c, i) => a + i%2 == 0 ? c : 0 );//10 + 30 + 50
}
可能不够简洁,但它一个函数代替了Where和Sum。所在位置“i“的引入给Aggregate带来了很多新的活力,也增加了它的应用范围!
我随笔《使用“初中知识”实现查找重复最优算法 + 最终极限算法》中最后提出的“最终极限算法”,用上这里改进的Aggregate扩展,也可以甩开Select和Sum,更加精简一步了:
{
//1~n放在含有n+1个元素的数组中,只有唯一的一个元素值重复,最简算法找出重复的数
int[] array = new int[] { 1, 3, 2, 3, 4, 5 };
//原极限算法
int repeatedNum1 = array.Select((i, j) => i - j).Sum();
//最新极限算法
int repeatedNum2 = array.Aggregate((a, n, i) => a + n - i);
}

-------------------
思想火花,照亮世界



