BST就是二叉搜索树(Binary Search Tree)的简称,因此毫无疑问BST也是二叉树,对于二叉树而言,和线性表的实现一样,我们也必须设计其数据节点,而且也必须设计其诸如插入、删除等操作。由于一般二叉树使用顺序存储会不可避免地浪费存储空间,因此我们一般都采用链式存储来表达一棵二叉树。
BST之所以称为二叉搜索树,是因为我们对其节点的存放位置做了严格的规定,从而来提高其搜索性能。BST规定:在任何子树中,根节点必须大于其左子树中任意的节点,且必须小于其右子树中任意的节点,换句话说必须满足“小 ---- 中 ----- 大”的逻辑次序。
树节点的设计,包括了三个要素:数据域、左孩子指针和右孩子指针,其代码如下:
struct node
{
datatype data;
struct node *lchild;
struct node *rchild;
};
有了树的结构体,我们就可以写出初始化一棵空BST和产生一个新节点的代码了。如下:
struct node * init_tree(void) //初始化一棵空BST
{
return NULL;
}
struct node * new_node(datatype data) //产生一个新节点
{
struct node *new = malloc(sizeof(struct node));
if(NULL != new)
{
new->data = data;
new->lchild = NULL;
new->rchild = NULL;
}
return new;
}
由于树本身是一种递归的结构,因此它的操作算法都可以用递归来实现。
算法实现和示例下面给出完整的代码实现,包括头文件和c文件。
首先是头文件: head4tree.h、head4queue.h、commonheader.h、drawtree.h
head4tree.h
//////////////////////////////////////////////////////////////////
// Description: 本文件为二叉树核心头文件。
// 任何使用本二叉树结构算法的程序,在包含本头文件之前
// 都需要将如下宏定义成二叉树节点需要表达的数据类型:
//
// TREE_NODE_DATATYPE
//
// 否则二叉树的节点数据类型一律默认为 int
//
//////////////////////////////////////////////////////////////////
#ifndef _HEAD4TREE_H_
#define _HEAD4TREE_H_
/*
* Any application applying this linked-tree data structure should
* define the macro "TREE_NODE_DATATYPE" before include this head
* file, otherwise, the macro will be defined to 'int' as follow.
*
*/
#ifndef TREE_NODE_DATATYPE
#define TREE_NODE_DATATYPE int
#endif
#include "commonheader.h"
#define MAX(a, b) ({ \
typeof(a) _a = a; \
typeof(b) _b = b; \
(void)(&_a == &_b);\
_a > _b? _a : _b; \
})
typedef TREE_NODE_DATATYPE tn_datatype;
#ifdef RB
#define RED 0
#define BLACK 1
#endif
typedef struct _tree_node
{
tn_datatype data;
struct _tree_node *lchild;
struct _tree_node *rchild;
#ifdef AVL
int height;
#endif
#ifdef RB
struct _tree_node *parent;
int color;
#endif
}treenode, *linktree;
void pre_travel(linktree, void (*handler)(linktree));
void mid_travel(linktree, void (*handler)(linktree));
void post_travel(linktree, void (*handler)(linktree));
void level_travel(linktree, void (*handler)(linktree));
linktree bst_insert(linktree root, linktree new);
linktree bst_remove(linktree root, tn_datatype data);
linktree bst_find(linktree root, tn_datatype data);
#ifdef AVL
linktree avl_insert(linktree root, linktree new);
linktree avl_remove(linktree root, tn_datatype data);
linktree avl_rotate_left (linktree root);
linktree avl_rotate_right(linktree root);
linktree avl_rotate_leftright(linktree root);
linktree avl_rotate_rightleft(linktree root);
static int height(linktree root)
{
return root==NULL ? 0 : root->height;
}
#endif
static linktree new_node(tn_datatype data)
{
linktree new = malloc(sizeof(treenode));
if(new != NULL)
{
new->data = data;
new->lchild = NULL;
new->rchild = NULL;
#ifdef AVL
new->height = 1;
#endif
#ifdef RB
new->parent = NULL;
new->color = RED;
#endif
}
return new;
}
#endif
head4queue.h
//////////////////////////////////////////////////////////////////
// Description: 本文件为队列核心头文件。
// 任何使用本队列算法的程序,在包含本头文件之前都需要
// 将如下宏定义成队列节点需要表达的数据类型:
//
// QUEUE_NODE_DATATYPE
//
// 否则队列的节点数据类型一律默认为 int
//
//////////////////////////////////////////////////////////////////
#ifndef _HEAD4QUEUE_H__
#define _HEAD4QUEUE_H__
#include "commonheader.h"
#ifndef QUEUE_NODE_DATATYPE
#define QUEUE_NODE_DATATYPE int
#endif
typedef QUEUE_NODE_DATATYPE qn_datatype;
struct _queue_node
{
qn_datatype data;
struct _queue_node *next;
};
typedef struct _queuenode
{
struct _queue_node *front;
struct _queue_node *rear;
#ifdef QUEUE_SIZE
int size;
#endif
}queuenode, *linkqueue;
bool is_empty_q(linkqueue);
bool out_queue(linkqueue, qn_datatype *);
bool en_queue(linkqueue, qn_datatype);
linkqueue init_queue(void);
#ifdef QUEUE_SIZE
int queue_size(linkqueue *);
#endif
#endif
commonheader.h
#ifndef _COMMONHEADER_H_
#define _COMMONHEADER_H_
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <unistd.h>
#include <string.h>
#include <strings.h>
#include <time.h>
#include <errno.h>
#include <sys/stat.h>
#include <sys/types.h>
#include <fcntl.h>
#include <sys/ipc.h>
#include <sys/sem.h>
#include <sys/shm.h>
#include <sys/msg.h>
#include <semaphore.h>
#include <fcntl.h>
#include <pthread.h>
#endif
drawtree.h
//////////////////////////////////////////////////////////////////
// Description: 使用C语言写一页webpage
//////////////////////////////////////////////////////////////////
#ifndef _DRAWTREE_H_
#define _DRAWTREE_H_
#include "commonheader.h"
#include "head4tree.h"
#ifndef QUEUE_NODE_DATATYPE
#define QUEUE_NODE_DATATYPE linktree
#endif
#include "head4queue.h"
static char page_begin[] = "<html><head><title>tree map"
"</title></head><body>"
"<table border=0 cellspacing"
"=0 cellpadding=0>";
static char line_begin[] = "<tr>";
static char line_end [] = "</tr>";
static char space [] = "<td> </td>";
static char underline [] = "<td style=\"border-bottom:"
"1px solid #58CB64\"> "
"</td>";
#ifdef RB
static char data_begin_red[] = "<td bgcolor=\"#FF0000\";style="
"\"border:1px sol"
"id #58CB64;background-colo"
"r:#DDF1D8;PADDING:2px;\" t"
"itle=\"level: 1\">";
static char data_begin_blk[] = "<td bgcolor=\"#000000\";style="
"\"border:1px sol"
"id #58CB64;background-colo"
"r:#DDF1D8;PADDING:2px;\" t"
"itle=\"level: 1\"><font color"
"=\"#FFFFFF\">";
static char data_end_red[] = "</td>";
static char data_end_blk[] = "</font></td>";
#else
static char data_begin[] = "<td style=\"border:1px sol"
"id #58CB64;background-colo"
"r:#DDF1D8;PADDING:2px;\" t"
"itle=\"level: 1\">";
static char data_end [] = "</td>";
#endif
static char page_end [] = "</table></body></html>";
#define MAX_NODES_NUMBER 100
#define FILENAME 32
static tn_datatype central_order[MAX_NODES_NUMBER];
void putunderline(int fd, int num);
void putspace(int fd, int num);
#ifdef RB
void putdata(int fd, linktree p);
#else
void putdata(int fd, int data);
#endif
int get_index(tn_datatype data);
void create_index(linktree root);
void data_leftside(int fd, linktree root, int spaces);
int data_rightside(int fd, linktree root);
void start_page(int fd);
void end_page(int fd);
void draw(linktree root);
#endif
drawtree提供的draw函数用来在webpage上面把树画出来。
然后是c文件:queue.c drawtree.c bst.c
queue.c
////////////////////////////////////////////////////////////////////
// Description: 链队列
////////////////////////////////////////////////////////////////////
#include "head4queue.h"
linkqueue init_queue(void)
{
linkqueue q = (linkqueue)malloc(sizeof(queuenode));
q->front = q->rear =
(struct _queue_node *)malloc(sizeof(struct _queue_node));
q->rear->next = NULL;
return q;
}
bool is_empty_q(linkqueue q)
{
return (q->front == q->rear);
}
bool out_queue(linkqueue q, qn_datatype *pdata)
{
if(is_empty_q(q))
return false;
struct _queue_node *p = q->front;
q->front = q->front->next;
free(p);
*pdata = q->front->data;
return true;
}
bool en_queue(linkqueue q, qn_datatype data)
{
struct _queue_node *pnew;
pnew = (struct _queue_node *)malloc(sizeof(struct _queue_node));
if(pnew == NULL)
return false;
pnew->data = data;
pnew->next = NULL;
q->rear->next = pnew;
q->rear = pnew;
return true;
}
#ifdef QUEUE_SIZE
int queue_size(linkqueue *q)
{
return q->size;
}
#endif
drawtree.c
////////////////////////////////////////////////////////////////////
// Description: 将二叉树的逻辑层次结构,用网页展示出来
////////////////////////////////////////////////////////////////////
#include "head4tree.h"
#include "drawtree.h"
void putunderline(int fd, int num)
{
int i;
for(i=0; i<num; i++)
{
write(fd, underline, strlen(underline));
}
}
void putspace(int fd, int num)
{
int i;
for(i=0; i<num; i++)
{
write(fd, space, strlen(space));
}
}
#ifdef RB
void putdata(int fd, linktree p)
{
char s[50];
bzero(s, 50);
snprintf(s, 50, "%d", p->data);
switch(p->color)
{
case RED:
write(fd, data_begin_red, strlen(data_begin_red));
write(fd, s, strlen(s));
write(fd, data_end_red, strlen(data_end_red));
break;
case BLACK:
write(fd, data_begin_blk, strlen(data_begin_blk));
write(fd, s, strlen(s));
write(fd, data_end_blk, strlen(data_end_blk));
}
}
#else
void putdata(int fd, int data)
{
char s[50];
bzero(s, 50);
snprintf(s, 50, "%d", data);
write(fd, data_begin, strlen(data_begin));
write(fd, s, strlen(s));
write(fd, data_end, strlen(data_end));
}
#endif
static int Index = 0;
void create_index(linktree root)
{
if(Index >= MAX_NODES_NUMBER-1)
return;
central_order[Index++] = root->data;
}
int get_index(tn_datatype data)
{
int i;
for(i=0; i<100; i++)
{
if(central_order[i] == data)
return i;
}
return -1;
}
void data_leftside(int fd, linktree root, int spaces)
{
if(root == NULL)
return;
int s_line=0;
if(root->lchild != NULL)
{
s_line = get_index(root->data)-
get_index(root->lchild->data)-1;
}
putspace(fd, spaces-s_line);
putunderline(fd, s_line);
}
int data_rightside(int fd, linktree root)
{
if(root == NULL)
return 0;
int s_line=0;
if(root->rchild != NULL)
{
s_line = get_index(root->rchild->data)-
get_index(root->data)-1;
}
putunderline(fd, s_line);
return s_line;
}
void start_page(int fd)
{
write(fd, page_begin, strlen(page_begin));
}
void end_page(int fd)
{
write(fd, page_end, strlen(page_end));
}
void draw(linktree root)
{
if(root == NULL)
return;
time_t t;
time(&t);
static char filename[FILENAME];
bzero(filename, FILENAME);
snprintf(filename, FILENAME, "%u.html", (unsigned)t);
int fd = open(filename, O_CREAT | O_TRUNC | O_RDWR, 0644);
if(fd == -1)
{
perror("open() failed");
exit(1);
}
Index = 0;
mid_travel(root, create_index);
linkqueue q = init_queue();
linktree tmp = root;
int ndata = 1;
start_page(fd);
while(1)
{
write(fd, line_begin, strlen(line_begin));
int i, n = 0;
int nextline = 0;
for(i=0; i<ndata; i++)
{
int index = get_index(tmp->data);
data_leftside(fd, tmp, index-n);
#ifdef RB
putdata(fd, tmp);
#else
putdata(fd, tmp->data);
#endif
int rightline = data_rightside(fd, tmp);
if(tmp->lchild != NULL)
{
nextline++;
en_queue(q, tmp->lchild);
}
if(tmp->rchild != NULL)
{
nextline++;
en_queue(q, tmp->rchild);
}
if(!out_queue(q, &tmp))
return;
n = index + rightline;
n++;
}
write(fd, line_end, strlen(line_end));
ndata = nextline;
}
end_page(fd);
close(fd);
}
bst.c
////////////////////////////////////////////////////////////////////
// Description: BST算法实现代码
////////////////////////////////////////////////////////////////////
#include "head4tree.h"
#include "drawtree.h"
linktree bst_insert(linktree root, linktree new)
{
if(new == NULL)
return root;
if(root == NULL)
return new;
if(new->data > root->data)
{
root->rchild = bst_insert(root->rchild, new);
}
else if(new->data < root->data)
{
root->lchild = bst_insert(root->lchild, new);
}
else
{
printf("%d is already exist.\n", new->data);
}
return root;
}
linktree bst_find(linktree root, tn_datatype data)
{
if(root == NULL)
return NULL;
if(data < root->data)
return bst_find(root->lchild, data);
else if(data > root->data)
return bst_find(root->rchild, data);
else
return root;
}
linktree bst_remove(linktree root, tn_datatype n)
{
if(root == NULL)
return NULL;
if(n < root->data)
root->lchild = bst_remove(root->lchild, n);
else if(n > root->data)
root->rchild = bst_remove(root->rchild, n);
else
{
linktree tmp;
if(root->lchild != NULL)
{
for(tmp=root->lchild; tmp->rchild!=NULL;
tmp=tmp->rchild);
root->data = tmp->data;
root->lchild = bst_remove(root->lchild, tmp->data);
}
else if(root->rchild != NULL)
{
for(tmp=root->rchild; tmp->lchild!=NULL;
tmp=tmp->lchild);
root->data = tmp->data;
root->rchild = bst_remove(root->rchild, tmp->data);
}
else
{
free(root);
return NULL;
}
}
return root;
}
int main(void)
{
linktree root;
root = NULL;
printf("输入大于0的数插入节点\n");
printf("输入小于0的数删除节点\n");
printf("输入0退出程序\n");
int n;
while(1)
{
scanf("%d", &n);
if(n > 0)
{
linktree new = new_node(n);
root = bst_insert(root, new);
}
else if(n < 0)
{
root = bst_remove(root, -n);
}
if(n == 0)
break;
draw(root);
system("firefox -new-tab *.html &");
}
system("rm *.html");
return 0;
}
该文件里面包含了测试入口函数main,实现了以下功能:
1、输入大于0的整数就插入节点
2、输入小于0的整数就删除其绝对值对应的节点
3、输入0就退出程序
4、退出程序之前用网页把这棵树画出来
运行效果如下:
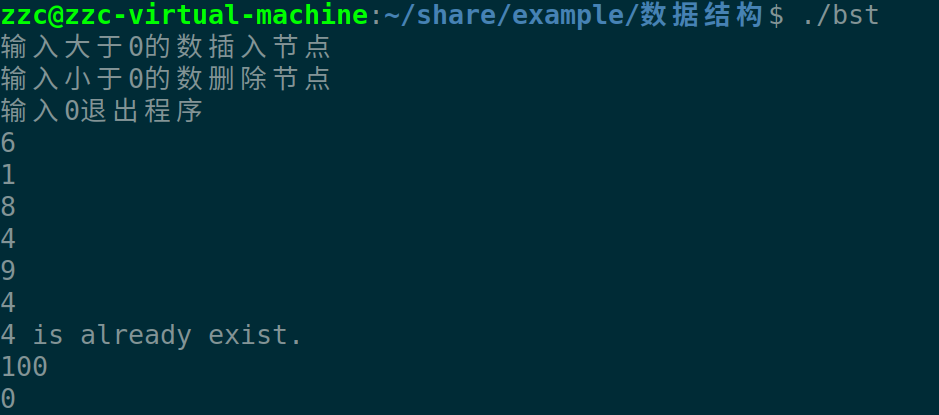
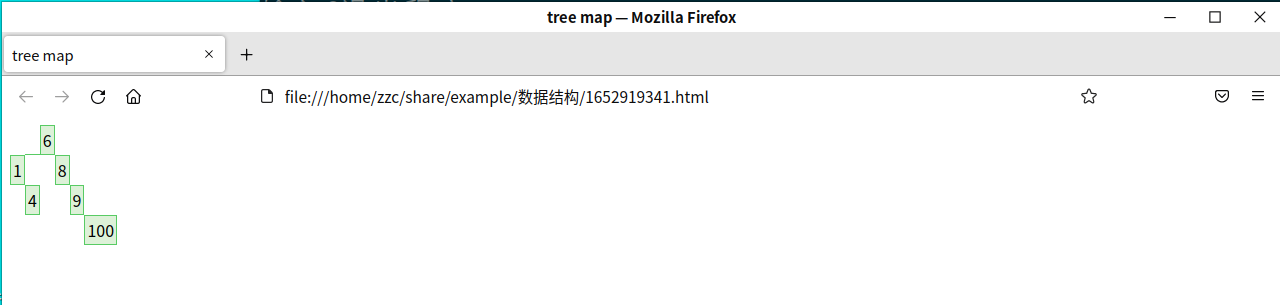
目前实现了最很简单的二叉搜索树,但是存在一个问题:这颗树可能会由于插入或删除的节点的随机性导致不平衡,从而影响BST的搜索性能。
什么是二叉树的不平衡?平衡树?红黑树?后面我有时间再一一道来。
总结本文简单介绍了BST树的概念,并提供了相关的算法实现,演示了运行效果。
后面我有时间会把平衡树和红黑树的知识点及算法实现补充进来,以便日后使用。
