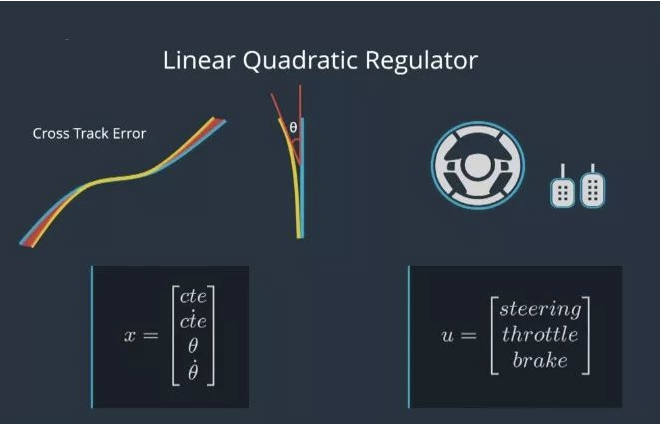
线性二次调节器(Linear Quadratic Regulator 或LQR)是基于模型的控制器,它使用车辆的状态来使误差最小化。Apollo使用LQR进行横向控制。横向控制包含四个组件:横向误差、横向误差的变化率、朝向误差和朝向误差的变化率。变化率与导数相同,我们用变量名上面的一个点来代表。我们称这四个组件的集合为X,这个集合X捕获车辆的状态。除了状态之外,该车有三个控制输入:转向、加速和制动。我们将这个控制输入集合称为U。
LQR处理线性控制,这种类型的模型可以用等式来表示(详见下图)。x(上方带点)=Ax+Bu,x(上方带点)向量是导数,或X向量的变化率。所以x点的每个分量只是x对应分量的导数。等式x点=Ax+Bu,该等式捕捉状态里的变化,即x点是如何受当前状态 x 和控制输入 u 的影响的。

这个等式是线性的,因为我们用∆x来改变x时,并用∆u来改变u。x点的变化也会让这个等式成立(见下图等式)。现在我们了解了LQR中的L。

接下来我们学习LQR中的Q。这里的目标是为了让误差最小化,但我们也希望尽可能少地使用控制输入。由于使用这些会有成本,例如:耗费气体或电力。为了尽量减少这些因素,我们可以保持误差的运行总和和控制输入的运行总和。当车往右转的特别厉害之际,添加到误差总和中。当控制输入将汽车往左侧转时,从控制输入总和中减去一点。然而,这种方法会导致问题。因为右侧的正误差只需将左侧的负误差消除即可。对控制输入来说也是如此。相反,我们可以让x和u与自身相乘,这样负值也会产生正平方,我们称这些为二次项。我们为这些项分配权重,并将它们加在一起。

最优的u应该最小化二次项的和随时间的积分。在数学中我们将这个积分值称为成本函数(形式见下图)。我们经常以紧凑的矩阵形式表示加权二次项的总和。

这里的Q和R代表x和u的权重集合。xT和uT是转置矩阵,这意味着它们几乎与x和u相同,只是重新排列以便矩阵相乘。x乘以xT,u乘以uT,实质上是将每个矩阵乘以它自己。最小化成本函数是一个复杂的过程,但通常我们可以依靠数值计算器为我们找到解决方案。Apollo就提供了一个这样的求解方案。在LQR中,控制方法被描述为u=-Kx。其中,K代表一个复杂的skeme,代表如何从x计算出u。所以找到一个最优的u就是找到一个最优的K。许多工具都可以轻松地用来解决K,尤其当你提供了模拟车辆物理特征的A、B,以及x和u的权重Q、R。
2.模型控制预测
模型预测控制(或MPC)是一种更复杂的控制器,它非常依赖于数学优化,但基本上可以将MPC归结为三个步骤:1、建立车辆模型。2、使用优化引擎计算有限时间范围内的控制输入。3、执行第一组控制输入。MPC是一个重复过程,它着眼未来,计算一系列控制输入,并优化该序列。但控制器实际上只实现了序列中的第一组控制输入,然后控制器再次重复该循环。为什么我们不执行整个控制输入序列呢?那是因为我们只采用了近似测量与计算。如果实现了整个控制输入序列,实际产生的车辆状态与我们的模型有很大差异,最好在每个时间步不断地重新评估控制输入的最优序列。
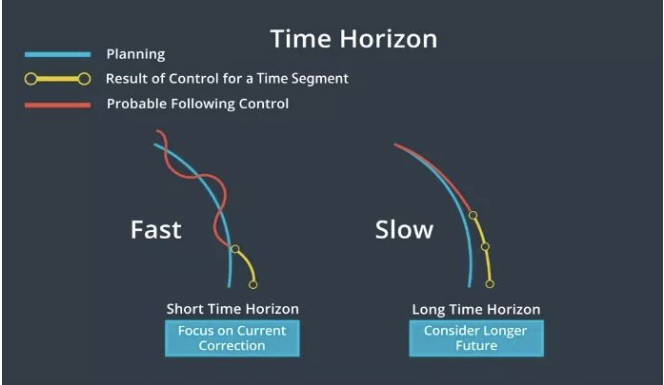
MPC的第一步为定义车辆模型,该模型近似于汽车的物理特性,该模型估计了假如将一组控制输入应用于车辆时会发生什么。接下来,我们决定MPC预测未来的能力。预测越深入,控制器就越精确,不过需要的时间也越长。所以,我们需要在准确度与快速获取结果之间做出取舍。获取结果的速度越快,越能快速地将控制输入应用到实际车辆中。
下一步是将模型发送到搜索最佳控制输入的优化引擎。该优化引擎的工作原理是通过搜索密集数学空间来寻求最佳解决方案。为缩小搜索范围,优化引擎依赖于车辆模型的约束条件。
优化引擎可间接评估控制输入,它通过使用以下方法对车辆轨迹进行建模:通过成本函数对轨迹进行评估。成本函数主要基于与目标轨迹的偏差;其次,基于其他因素,如加速度和提升旅客舒适度的措施。

为使乘客感觉更舒适,对控制输入的调整应该很小。因为动作变化幅度过大会让乘客感到不舒服。根据具体情况,我们可能需要为其考虑进一步的成本,并设计成本函数。模型、约束和成本函数合并在一起,并作为优化问题加以解决。我们可以在不同的优化引擎中,选择一种来寻找最佳解决方案。
3.总结
控制实际上是无人驾驶汽车实现自动移动的方式。在控制中,我们使用转向、加速和制动来运行我们的目标轨迹。我们研究了几种不同类型的控制器。PID控制是一种简单而强大的控制算法,线性二次调节器和模型预测控制是另外两种类型的控制器,它们更复杂,但也更强大、更准确。Apollo支持所有这三种控制器,而你也可以选择最适合自己的控制器!
