算法:算法是在有限步骤内求解某一问题所使用的一组定义明确的规则,通俗点说,就是计算机解题的过程
一个算法应该具有以下五个重要的特征:
1、有穷性: 一个算法必须保证执行有限步之后结束;
2、确切性: 算法的每一步骤必须有确切的定义;
3、输入:一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定除了初始条件;
4、输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法是毫无意义的;
5、可行性: 算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。
结构化算法:由一些顺序、选择、循环等基本结构按照顺序组成,流程的转移只存在于一个基本的范围之内。
结构化算法便于编写,可读性高,修改和维护起来简单,可以减少程序出错的机会,提高了程序的可靠性,保证了程序的质量,因此提倡结构化的算法。
3. 试述3种基本结构的特点,请另外设计两种基本结构(要符合基类结构的特点)。结构化程序设计方法主要由以下三种基本结构组成:
顺序结构:顺序结构是一种线性、有序的结构,它依次执行各语句模块
选择结构:选择结构是根据条件成立与否选择程序执行的通路。
循环结构:循环结构是重复执行一个或几个模块,直到满足某一条件位置
重新设计基本结构要满足以下几点:
只有一个入口
只有一个出口
结构内的每一部分都有机会执行到
结构内不存在死循环
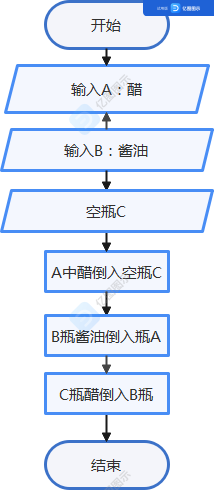
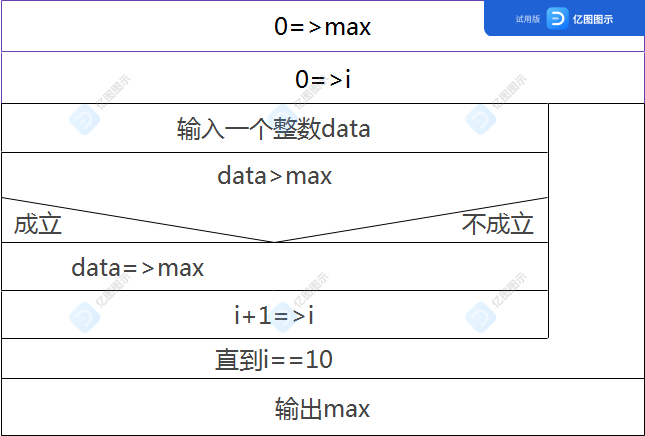
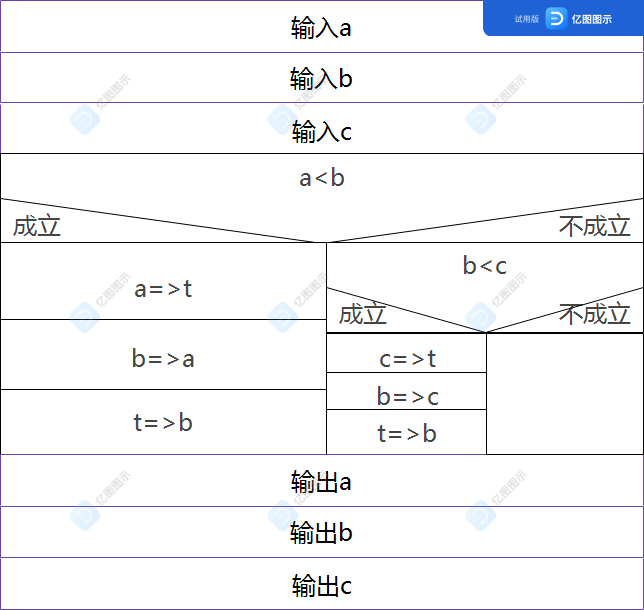

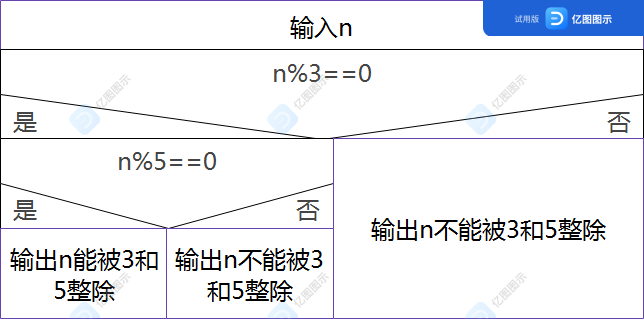
6. 用伪代码表示以下问题的算法。 1.有两个瓶子A和B,分别盛放醋和酱油,要求将他们互换(即A瓶原来盛醋,现在盛酱油,B瓶则相反)
begin
醋=>A
酱油=>B
A=>C
B=>A
C=>B
end
2.依次将10个数输入,要求输出其中最大的数begin
0=>i
0=>max
while i<10
{
输入一个整数data
if data>max
data=>max
i+1=>i
}
print max
end
3.有3个数a,b,c, 要求按大小顺序把他们输出begin
input a
input b
input c
if a<b
a=>t
b=>a
t=>b
if c>a
c=>t
a=>c
t=>a
print a
print b
print c
end
4.求1 + 2 + 3 + … + 100begin
0=>i
0=>sum
while i<100
sum+i=>sum
i+1=>i
print sum
end
5.判断一个数n能否同时被3和5整除begin
input n
if n%c==0
{
if n%5==0
{
print n能被3和5整除
}
else
{
print n不能被3和5整除
}
}
else
{
print n不能被3和5整除
}
end
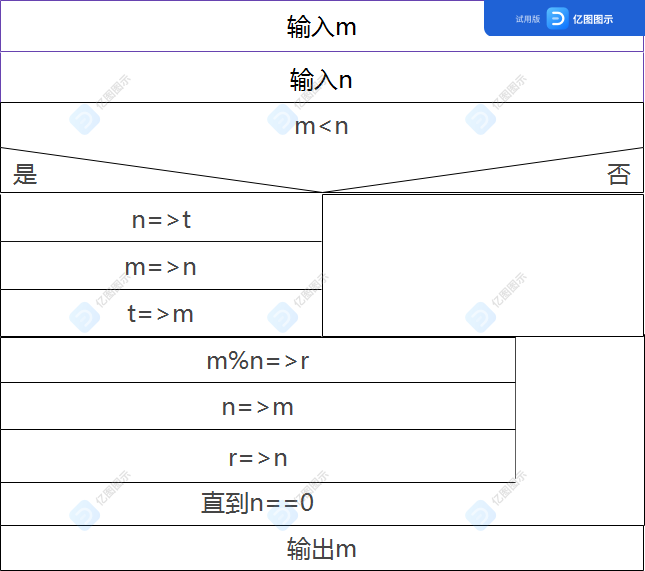
6.求两个数m和n的最大公约数begin
input m
input n
if m<n
{
m=>r
m=>n
r=>m
}
while n!=0
{
m%n=>t
n=>m
t=>n
}
print m
end
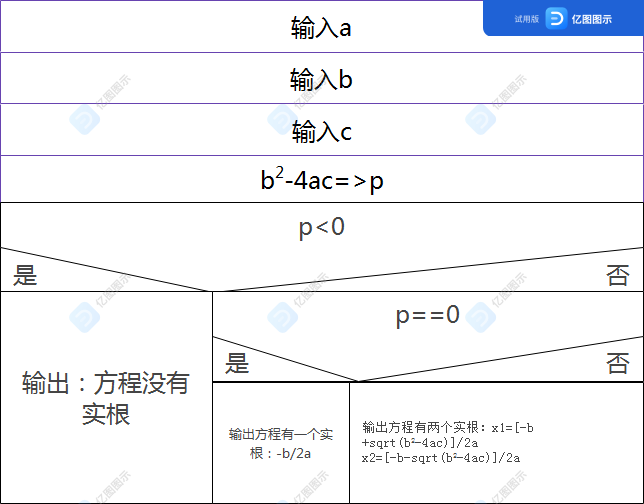
7.求方程ax2+bx+c=0的根。分别考虑: 1.有两个不相等的实根; 2.有两个相等的实根;begin
input a
input b
input c
b*b-4*a*c=>p
if p<0
{
print 没有实根
}
if p==0
{
print 方程有一个实根 -b/2*a
}
else
{
print 方程有两个实根:
print x1=[-b+sqrt(b2-4ac)]/2a
print x2=[-b-sqrt(b2-4ac)]/2a
}
end
7. 什么叫结构化程序设计?它的主要内容是什么?结构化程序设计(structured programming,简称SP)是进行以模块功能和处理过程设计为主的详细设计的基本原则。其概念最早由E.W.Dijikstra在1965年提出的。
结构化程序设计思想确实使程序执行效率提高 ,是软件发展的一个重要的里程碑,它的主要观点是采用自顶向下、逐步求精的程序设计方法;各个模块通过“顺序、选择、循环”的控制结构进行连接,并且只有一个入口、一个出口 。
8. 用自顶向下、逐步细化的方法进行以下算法的设计: 1.输出1900—2000年中是软黏的年份,符合下面两个条件之一的年份是闰年: 能被4整除但不能被100整除 能被100整除且能被400整除。 2.求ax2+bx+c=0的根。分别考虑d=b2−4ac大于0、等于0和小于0这三种情况。 3.输入10个数,输出其中最大的一个数。
1.
算法流程 1. 循环选取1900到2000中的每一个年份 2. 对于每一个年份判断其是否为闰年 3. 是闰年则输出次年份 判断年份是否为闰年: 1. 如果该年份被4整除但是不能被100整除则为闰年,否则不是闰年 2. 如果年份能被400整除则为闰年,否则不是闰年
2.
1. 获取a b c的值 2. 计算b^2 - 4ac的结果并赋给p 3. 如果p < 0, 则方程没有实根 4. 如果p == 0,则方程有一个实根-b/2a 5. 如果p > 0, 则方程有两个实根 x1 = {-b + sqrt(b^2 - 4ac)}/2a ,x2 = {-b - sqrt(b^2 - 4ac)}/2a
3.
1. 设定一个max变量保存最大值 2. 分别输入10个数,并依次把每个数与max进行比较 如果该数大于max,则将该数赋值给max 3. 输出max
