【ACM程序设计】动态规划 第一篇 引入

动态规划

[P1216 USACO1.5][IOI1994]数字三角形 Number Triangles - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

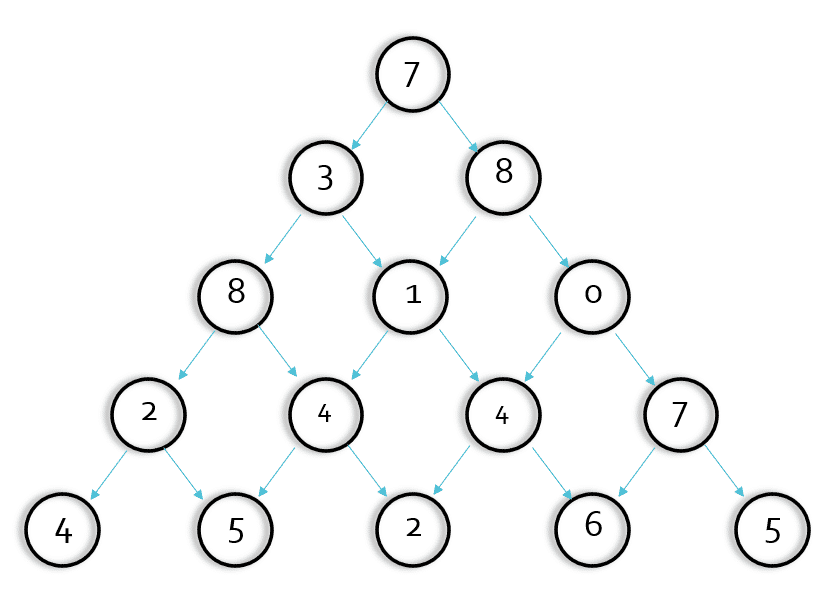
观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

        7 
      3   8 
    8   1   0 
  2   7   4   4 
4   5   2   6   5 

在上面的样例中，从 7→3→8→7→5 的路径产生了最大

输入格式

第一个行一个正整数 r ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

输入输出样例

输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5 

输出 #1

30

说明/提示

【数据范围】
对于 100% 的数据，1≤ r ≤1000，所有输入在 [0,100] 范围内。

因为题目的样例用贪心就能过,所以将样例稍作改编

输入 #2

5
7
3 8
8 1 0
2 4 4 7
4 5 2 6 5

输出 #2

28

• 我们大部分人看到这道题脑海中都会浮现这样的想法，是不是只要每步走的都是两个点中较大的那个值，最后的答案就是最大的。就像这样：7->8->1->4->6
• 我们会发现在第四步的时候情况不对，这里两个子节点相同,明显取右侧的4比左侧的4结果要大，可是当程序执行到这一步，我们要如何使计算机明白要选择右边的结点而不是左边的。

贪心策略

这种做法其实是一种贪心的思想,来看它的定义：

• 贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

我们会发现,即使在第四步选择了右边这个点,结果(7->8->1->4->6=26)比题目给出的答案7->8->0->7->6总和为28小.即题目在第三层就选择了小的0而不是1。

正是因为我们每次选择的时候只考虑当前的物品而没有考虑后面的物品,而产生的决策错误.

因此我们可以知道贪心策略的限制条件，每次选择局部最优解的时候，一定要保证局部最优策略不会对后续决策产生影响，如此才能使用贪心策略。

搜索算法

我们再来考虑一种方法,既然贪心行不通,我们不妨考虑通过搜索来获得它所有的结果.

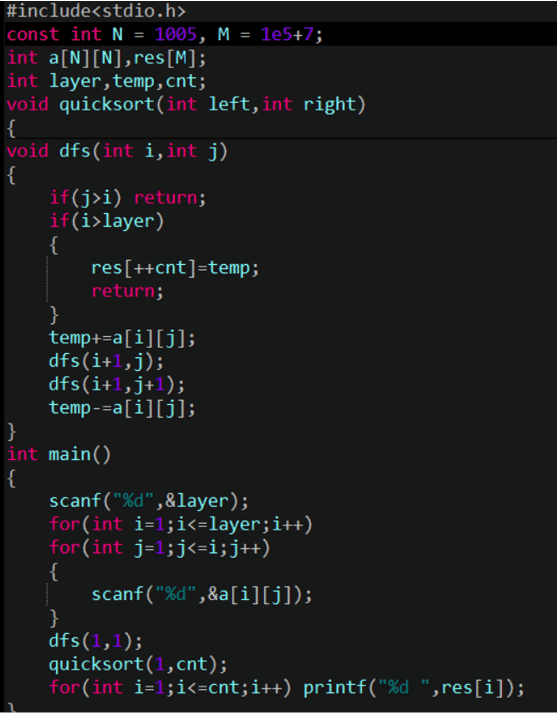
然而，会发现：在每一层每个结点都有两种选择,选择左下或者右下，那么数字三角形有 2^n-1条路线,我们既需要O(2^n-1)的时间,又需要2^n-1的空间，如果不进行剪枝当层数很大的时候这是行不通的。

我们考虑一下能不能把搜索优化。

首先,回到刚才那个想法，在第 4 层 4 和 4 相同的情况下到底计算机应该选择哪一个。此时，我们可以考虑让计算机分别对这两个结点进行搜索，搜索完再返回大的值，即我们要选择的结点。

接着，我们想这种想法可不可以在两个结点不相同的时候也使用。于是就有了我们从第一个结点开始，往下先对3和8进行搜索，3和8再分别对自己的子节点搜索…………搜索完后逐层向上返回最大值，这样使得计算机在每次决策的时候选择的都是最优的。

可惜,我们会发现,这个时间复杂度还是O(2^n-1)，因为还是每个结点要对底下的两结点搜索。

NOT GIVE UP

我们反思一下刚才的递归算法

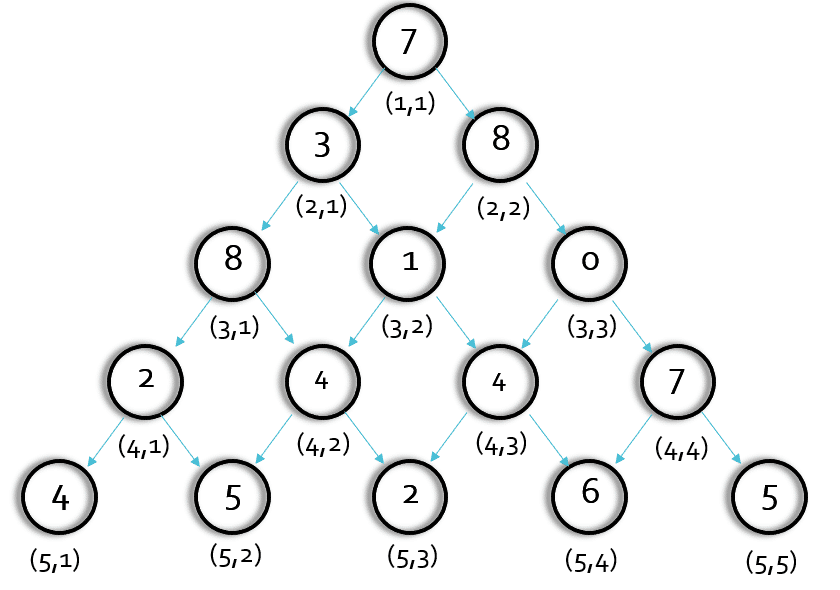
我们先把图简化，我们看第三层，是不是(2,1)和(2,2)均要执行一次solve(3,2)这个函数，即(3,2)这个点将要被执行两次。

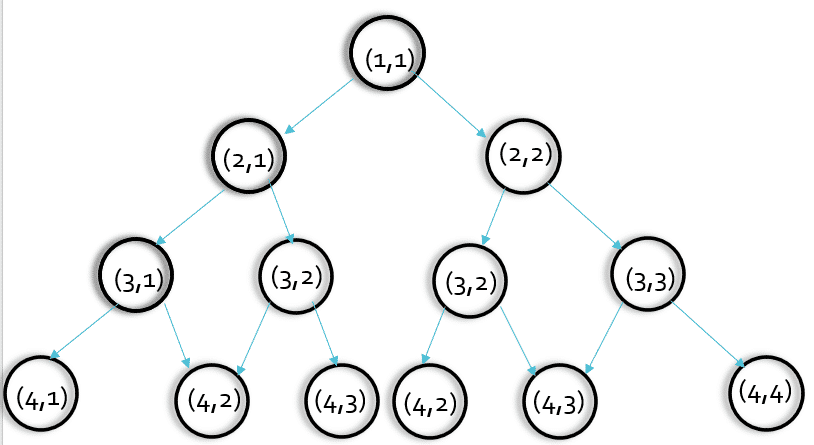
可能我们会认为，重复算一两个数影响不大，但是,我们以此类推，会发现(3,2)的子节点也会被搜索多次，这样，当层数很多时重复搜索的次数会很多，导致了时间的浪费(这就是-----重叠子问题)

我们想想，有什么方法可以防止重复搜索。

• a：当然是把它记下来！

我们考虑用一个二维数组 d[ i ][ j ] 来记录这个递归的返回值。

int solve(int i,int j)
{
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

记录好了，应该如何让计算机明白“已经计算过了,不用再计算了”?

int solve(int i,int j)
{
    if(d[i][j]>=0) return d[i][j];
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

当 d[i][j] == 0 时表示已经计算过了，如果 d 数组初值为 0，每次搜索都会直接返回，所以我们还需要给d数组赋上初值，即在int main()函数中加入这样一句。

memset(d,-1,sizeof d);

这就是记忆化搜索

由于我们储存了每个结点递归的返回值，我们可以保证每个结点只被递归计算一次。所以时间复杂度是O(n²)，从2ⁿ~n²这是一个巨大的优化。

int solve(int i,int j)
{
    if(d[i][j]>=0) return d[i][j];
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

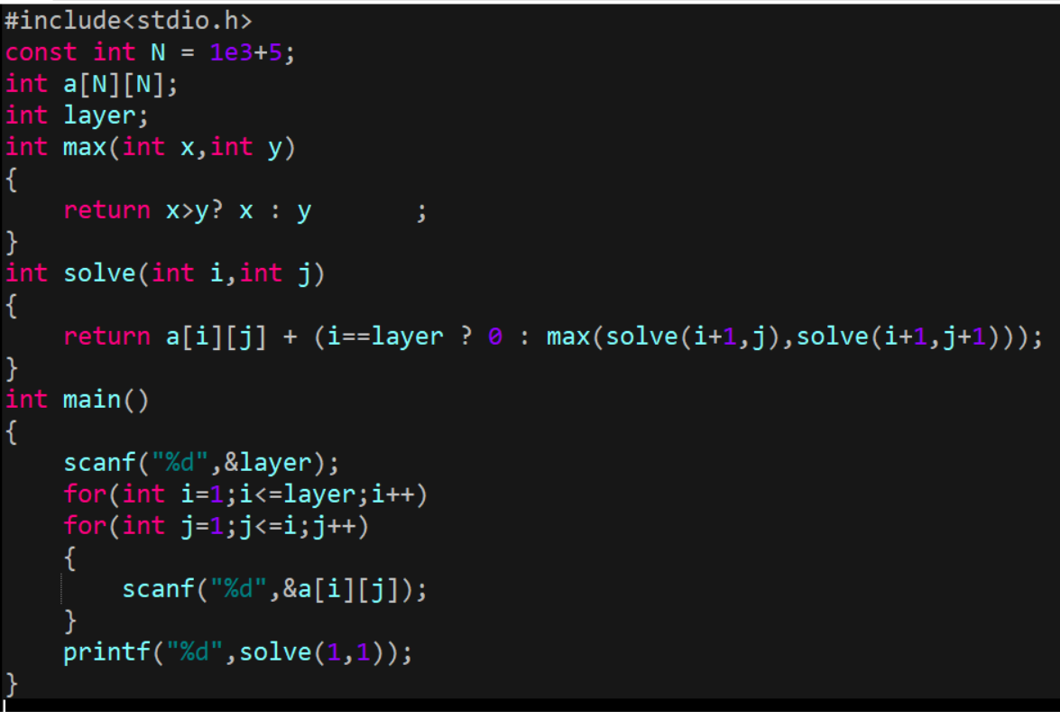
我们来考虑d(i,j)这个数组的意义，可以发现d(i,j)表示这个位置出发能得到的最大和(包括本身)。

我们把d(i,j)当成一个函数，那么原问题就可以是求解d(1,1)这个值，即代入下面这个数学函数。

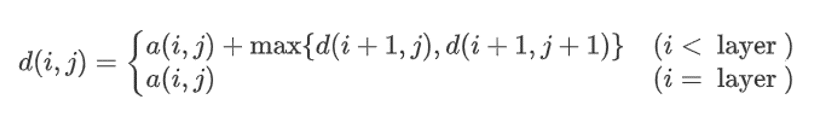
这样,我们就引出了今天的主角-----动态规划

什么是动态规划？

• 动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著《Dynamic Programming》，这是该领域的第一本著作。--------百度百科

简单来说，dp是具有递推形式的记忆化搜索，其核心思路是将大问题转化为可以重复被调用最优解的子问题并最终递推出题目整体最优解。

在动态规划的概念里，我们把d(i,j)定义为一个”状态”，而这个方程就是所谓的”状态转移方程”。

而这个状态体现的从 ( i , j ) 出发的最大总和，正是”最优子结构”，即”全局最优解包含局部最优解”，这就有效解决了贪心算法中(局部最优解不一定是整体最优解)的问题。

在上面的记忆化搜索中，我们求解的方式是从方程左边到方程右边，而动态规划正相反，从右边推出左边。

最后呈现的正是计算机决策的路径。这一方法被我们称为”递推”。

总结

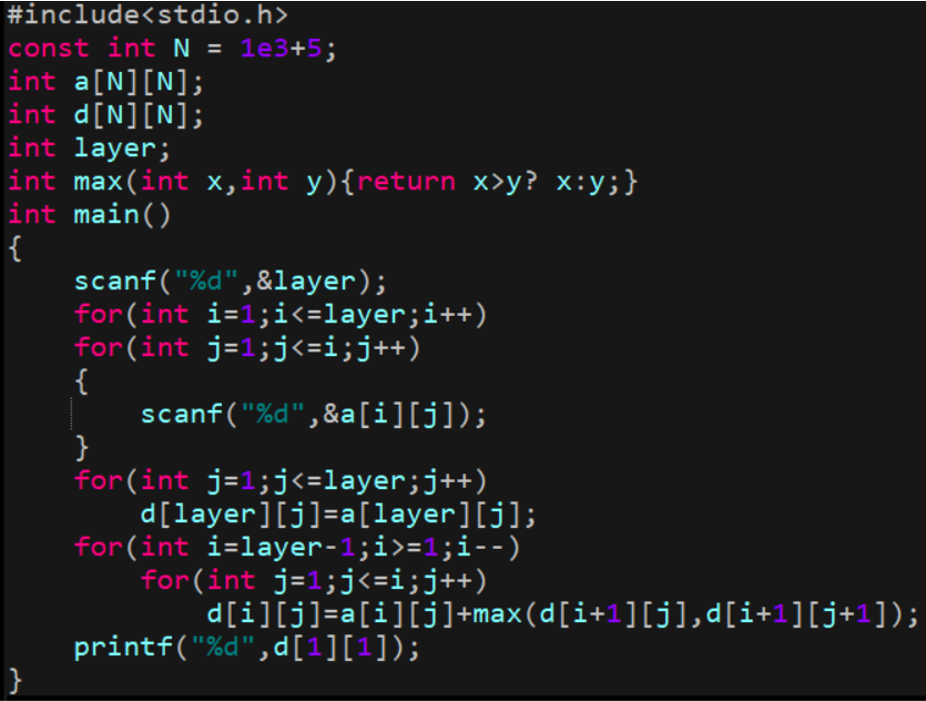
动态规划的要素：1.初始状态 2.递推关系公式

动态规划的特征：1.最优子结构 2.无后效性 3.重复子问题

最优子结构：问题的最优解包含子问题的最优解

无后效性：某阶段状态只关心前面阶段的状态值。一旦确定，就不受之后阶段的决策影响。

重复子问题： 不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。