题解借鉴两位大佬的解析 墨染空 野生铅笔 本题是一道 01背包 的扩展题 —— 二维费用01背包问题 把 野生宝可梦 看做物品,则捕捉他需要的 精灵球 个数就是 第一费用 ,战斗 皮神要掉
题解借鉴两位大佬的解析 墨染空 && 野生铅笔
本题是一道 01背包 的扩展题 —— 二维费用01背包问题
把 野生宝可梦 看做物品,则捕捉他需要的 精灵球 个数就是第一费用,战斗皮神要掉的血就是第二费用
在背包问题中,体积w与价值v是可以互逆的!
可以将f[i]表示为体积为i能装的最大价值,
也可以将f[i]表示为价值为i所需的最小体积。
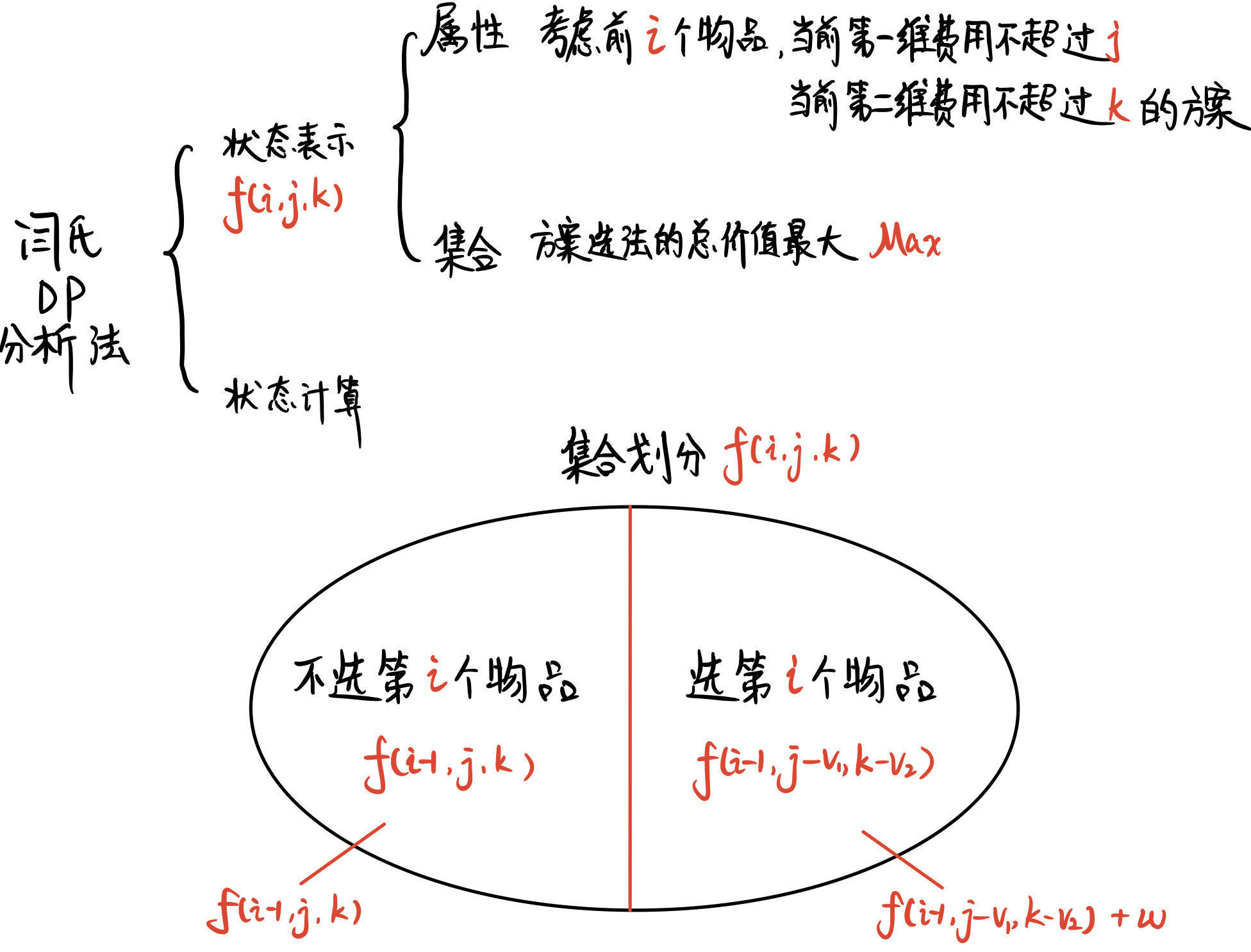
以上就是本题的 阅读理解分析部分 ,接下来直接上闫氏DP分析法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 1010, K = 510;
int n, m, t;
int v1[N], v2[N];
int f[M][K];
int main()
{
cin >> m >> t >> n;
for (int i = 1; i <= n; ++ i) cin >> v1[i] >> v2[i];
// 相当于优化;
for (int i = 1; i <= n; ++ i)
{
for (int j = m; j >= v1[i]; -- j) //倒序输出
{
for (int k = t - 1; k >= v2[i]; -- k)
{
f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
}
}
}
cout << f[m][t - 1] << " "; // 之所以是 t-1 是因为最坏的情况下皮卡丘也要剩余一滴血
int k = t - 1; // 倒退 剩余的最大血量
while (k > 0 && f[m][k - 1] == f[m][t - 1]) k -- ;
cout << t - k << endl;
return 0;
}
初始状态 : f[0][0][0]
目标状态: f[n][m][t-1]
