认识大O表示法
企业规模的概述:
公司可以按照规模分为:小型企业/中型企业/大型企业
在不说明具体员工人数或者占地面积的情况下,我们可以通过这样大概的概念来描述企业的规模
大O表示法:
在算法的描述中,我们也可以通过类似的快捷方式来描述计算机法的效率
在计算机中,这种粗略的度量被称作“大O”表示法
在算法比较的过程中,我们可能更喜欢说:算法A比算法B快两倍,但是这样的比较有时候没有意义
在数据项个数发生变化时,算法的效率会跟着发生改变
所以我们通常使用一种 算法的速度 会如何跟随着数据量的变化的
我们一起来认识一下,常见的大O表示函数
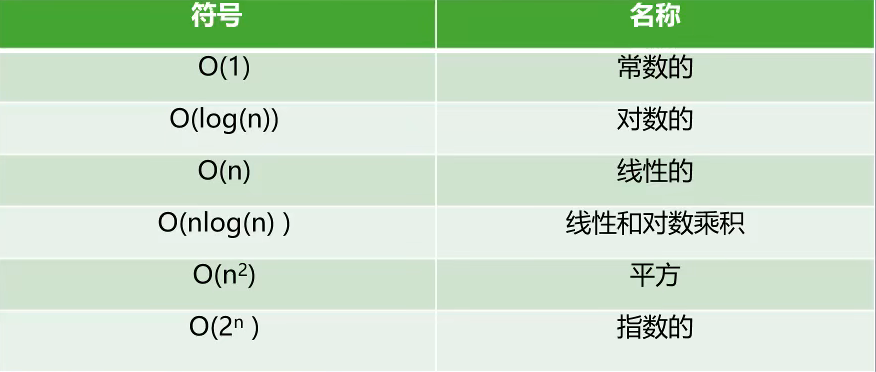
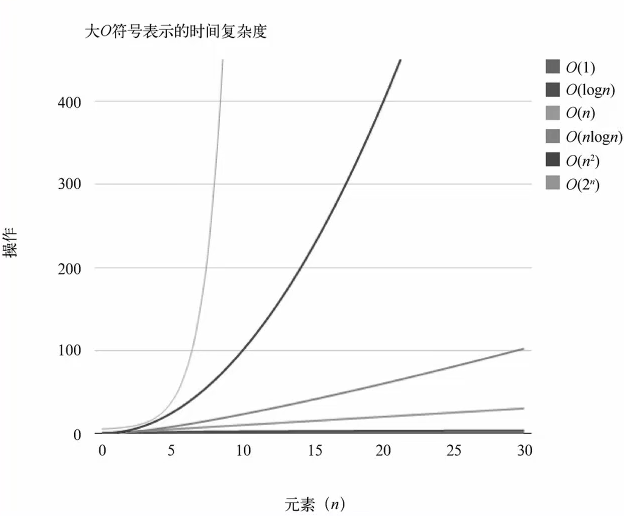
2N方+3n +1
O(2N方)
推导大O表示法的方式:
用常量1取代运行时间中所有的加法常量
在修改后的运行次数函数中,只保留最高阶项
如果最高存在且不为1,则去除与这个项相乘的常数
冒牌排序的效率
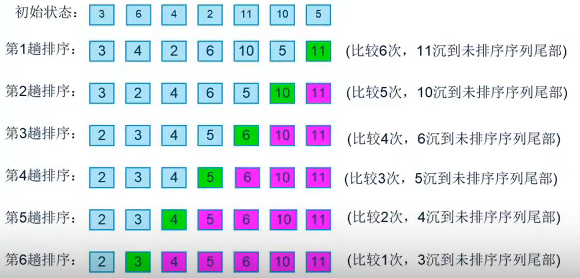
冒泡排序的比较次数
如果按照上面的例子来说,一共有7个数字,那么每次循环时进行了几次的比较呢?
第一次循环6次比较,第二次5次比较,第三次4次比较…直到最后一趟进行了依次比较
对于7个数据项比较次数:6 + 5 + 4 + 3 + 2 + 1
对于N个数据项呢?(N - 1) + (N - 2)+(N - 3)+ … + 1 = N * (N - 1)/ 2
通过大O表示法推到过程,我们来推到一下冒泡排序的大O形式:
N * (N - 1) / 2 = N方 / 2 - N / 2,只保留最高阶项,编程 N方 / 2
N方 / 2,根据规则3,去除常量,编程N方
因此冒牌排序的大O表示法为O(N方)
冒牌排序的交换次数:
冒牌排序的交换次数是多少呢?
如果有两次比较才需要交换一次(不可能每次比较都交换一次)那么交换次数为N方 / 4
由于常量不算在大O表示法中,因此,我们可以认为交换次数的大O表示也是O(N方)
认识排序算法
排序算法是笔试中经常出现的
排序算法有很多:冒泡排序/选择排序/插入排序/归并排序/计数排序(counting sort)/计数排序(radix sort)/希尔排序/堆排序/桶排序
我们这里不一一举例它们的实现思想,而是选择几个简单排序和高级排序
简单排序:冒泡排序 - 选择排序 - 插入排序
高级排序:希尔排序 - 快速排序
其他排序的理论和思想,大家可以自行学习
一旦我们将数据放置在某个数据结构中存储起来后(比如数组),就可能根据需求对数据进行不同的方式排序
比如对姓名按字母排序
对学生按年龄排序
对商品按照价格排序
对城市按照面积或者人口数量排序
如何排序?
由于排序非常重要而且可能非常耗时,所以它已经成为一个计算机科学中广泛研究的课题
而且人们已经研究出一套成熟得方案来实现排序
因此,幸运的是你并不需要是发明某种排序算法,而是站在巨人的肩膀上即可
如何排序?
需要:对一组身高不等的10个人进行排序
人来排序:
如果是人来排序事情会非常简单,因为人只要扫过去一眼就能看出来谁最高谁最低
然后让最低(或者最高)的站在前面,其他人依次后移
按照这样的 方法,依次类推就可以了
人排序的特点:
可以统筹全局,直接获取到最高或者最低的结果
不需要考虑空间和问题,因为通常情况下都有足够的空间来互相推嚷
计算机来排序:
计算机有些笨拙,它只能执行指令,所以没办法一眼扫过去
计算机也很聪明,只要你写出了正确的指令,可以让它帮你做无数次类似的事情而不用担心出现错误
并且计算机怕排序也无需担心数据量的大小
(想象一下,让人排序10000个,甚至更大的数据项你还能一眼扫过去吗?)
人在排序是不一定要固定特有的空间,他们可以互相推推嚷嚷就腾出来位置,还能互相前后站立
但是计算机必须有严密的逻辑和特定的指令
计算机的排序特点:
计算机不能像人一样,一眼扫过去这样通览所有的数据
它只能根据计算机的比较操作原理,在同一时间对两个队员进行比较
在人类看来很简单的事情,计算机的算法却不能看到全景
因此,它只能一步步解决具体问题和遵循一些简单的规则
封装列表
在开始排序之前,我们先来创建一个列表封装我们的数据项
// 创建列表类
function ArrayList() {
// 属性
this.array = []
// 方法
// 将数据可以插入到数组种的方法
ArrayList.prototype.insert = function(item) {
this.array.push(item)
}
// toString
ArrayList.prototype.toString = function() {
return this.array.join('-')
}
}
// 测试类
var list = new ArrayList()
// 插入元素
list.insert(66)
list.insert(88)
list.insert(65)
list.insert(54)
list.insert(34)
list.insert(232)
list.insert(332)
alert(list)
console.log(list)
冒泡排序的思路
冒泡排序算法相对其他的排序运行效率较低,但是在概念上它是排序算法中最简单的
因此,冒泡排序是在刚开始学习排序时,最适合学习的一种排序方式
冒泡排序的思路:
对未排序的个元素从头到尾依次比较的两个元素的大小关系
如果嘴边的队员高,则两队员交换位置
向右移动一个位置,比较下面两个队员
当走到最右端时,最高的队员一定被放在了最右边
按照这个思路,从最左端重新开始,这次走到倒数第二个位置的队员即可
依次类推,就可以将数据排序成功

代码思路分析
代码思路分析:
第一次找出最高人放在最后,我们需要两个两个数据项进行比较,那么这个应该时一个循环操作
第二次将次高的人找到放在倒数第二个位置,也是两个比较,只是不要和最后一个比较(少了依次),但是前面的
两个两个比较也是一个循环操作
第三次…第四次…
有发现规律吗?这应该是一个循环中嵌套循环,并且被嵌套的循环次数越来越少的
根据这个分析,你能写出代码实现吗?
// 交换两个位置的数据
ArrayList.prototype.swap = function(m, n) {
let temp = this.array[m]
this.array[m] = this.array[n]
this.array[n] = temp
}
// 实现排序算法
// 冒泡排序
ArrayList.prototype.bubblesort = function() {
// 获取数组长度
let length = this.array.length
// 第一次:j = length - 1,比较到倒数第一个位置
// 第二次:j = length - 2,比较到倒数第二个位置
// …
for (let j = length - 1; j >= 0; j--) {
// 第一次进来: i = 0买比较 0 和 1 位子的两个数据,如果 0 位置大于 1 位置的数据
// 最后一次进来: i = length - 2,比较 length - 2 和length - 1 的两个数据
for (let i = 0; i < j; i++) {
if (this.array[i] > this.array[i + 1]) {
this.swap(i, i + 1)
}
}
}
}
代码解析:
代码序号1:获取数组的长度
代码序号2:我们现在要写的外层循环,外城循环应该让i依次减少,
因此我们这里使用了反向的遍历
代码需要3:内层循环,内层循环我们使用 j < i ,因为上面的 i 在不断
减少,这样就可以控制内层循环的次数
代码需要4:比较两个数据项的大小,如果前面的大,那么就进项交换
选择排序的思路
选择排序改进了冒泡排序
将交换的次数由O(N方)减少到O(N)
但是比较的次数依然是O(N方)
选择排序的思路:
选定第一个索引位置,然后和后面元素依次比较
如果后面队员,小于第一个索引位置的队员,则交换位置
经过一轮的比较后,可以确定第一个位置是最小的
然后使用同样的方式把剩下的元素逐个比较即可
可以看出选择排序,第一轮会选出最小值,第二轮会选出第二小的值,直到最后

// 选择排序
ArrayList.prototype.selectionSort = function() {
// 获取数组的长度
let length = this.array.length
// 2
for (let j = 0; j < length - 1; j++) {
let min = j
for (let i = min + 1; i < length; i++) {
if (this.array[min] > this.array[i]) {
min = i
}
}
this.swap(min, j)
}
}
代码解析:
代码序号1:依然获取数组的长度
代码序号2:外层循环,我们已经进过,需要从外层循环的第0个位置开始,
依次遍历到length - 2的位置
代码序号3:先定义一个min,用于记录最小的位置,内层循环,内层循环是从
i + 1位置开始的数据项,和 i 位置的数据项依次比较,直到 length - 1 的数据项
代码序号4:如果比较的位置 i 数据项,大于后面某一个数据项,
那么记录最小位置的数据
代码序号5:将min位置的数据项,那么 i 位置的数据教官,那么 i 位置就是正确的数据了
注意:这里的监管是基于之前的交换方法,这里直接调用即可
选择排序的效率
选择排序的比较次数:
选择排序和冒泡排序的比较次数都是N*(N - 1)/2,也就是O(N方)
选择排序的交换次数:
选择排序每次进行选择的时候,最多需要交换1次,一共遍历多少次呢?N - 1次
选择排序的交换次数只有N - 1,用大O表示法就是O(N)
所以选择排序通过认为在执行效率上是高于冒泡排序的
插入排序的思路
插入排序是简单排序中效率最高的一种
插入排序也是学习其他高级排序的基础,比如希尔排序/快速排序,所以也非常重要
插入排序的思路
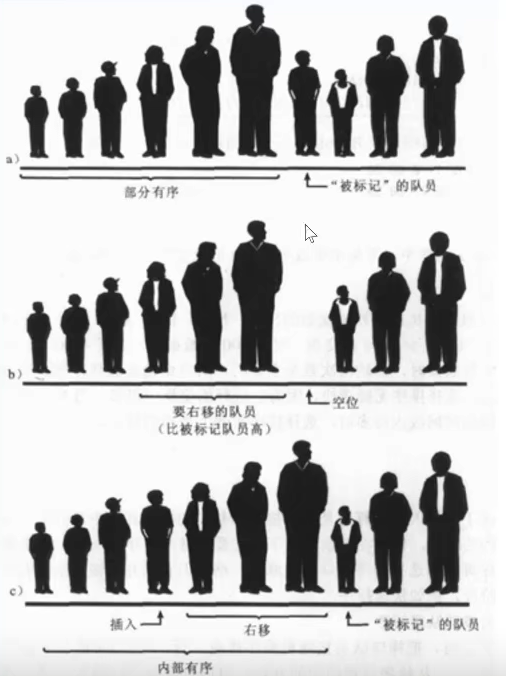
局部有序:
插入排序思想的核心是局部有序,什么是布局有序呢?
比如在一个队列中的人,我们选择其中一个作为标记的队员
这个被标记的队员左边的所有队员已经是局部有序的
这意味着,有一部门人是按顺序排序好的,有一部分还没有顺序
插入排序的思路:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复上一个步骤,直到找到已排序的元素大于或者等于新元素的位置
将新元素插入到该位置后,重复上面的元素
插入排序代码
// 插入排序
ArrayList.prototype.insertionSort = function() {
// 获取数组的长度
let length = this.array.length
// 外层循环,从第1个位置开始获取数据,向前面布局有序进入插入
for (let i = 1; i < length; i++) {
// 内层循环:获取i位置的元素,和前面的数据依次进行比较
let temp = this.array[i]
let j = i
while (this.array[j - 1] > temp && j > 0) {
this.array[i] = this.array[j - 1]
j--
}
// 将j位置的数据,放置temp就可以啦
this.array[j] = temp
}
}
代码思路分析
插入排序应该从下标值1开始(一位内0位置默认可以被认为是有序的)
从1位置开始取出元素,并且判断该元素的大小和0位置进行比较,如果1位置元素小于0位置元素,那么交换,否则不交换
从上面步骤执行完成后,0 - 1位置已经排序好
取出2位置的元素,和1位置进行比较
如果2位置元素小于1位置元素,说明2位置不需要任何动作。0 - 1 - 2已经排序好
如果2位置元素大于1位置元素,那么将1移动到2的位置,并且2继续和0进行比较
如果2位置元素大于0位置的元素,那么将2位置放置在1的位置,排序完成 0 - 1 - 2搞定
如果2位置元素小于1位置的元素,那么将0位置的元素移动到1位置,并且将2位置的元素放在0位置,0 - 1 - 2 搞定
按照上面的步骤,依次找到最后一个元素,整个数组排序完成
经常上面的分析,你能转化成对应的代码吗?
插入排序的效率
插入排序的比较次数:
第一趟时,需要的最多次数是1,第二趟最多次数是2,依次类推,最后一趟是N-1次
因此是 1 + 2 + 3 + … + N - 1 = N * (N - 1) / 2
然而每趟发现插入点之前,平均只有全体数据项的一半需要进行比较
我们可以除以2得到N * (N - 1) / 4,所以相对于选择排序,其他比较次数是少了一半的
插入排序的复制次数:
第一趟时,需要的最多复制次数是1,第二趟最多次数是2,依次类推,最后一趟是N-1次
因此是1 + 2 + 3 + … + N - 1 = N * (N - 1) / 2
对于基本有序的情况
对于已经有序或基本有序的数据来说,插入排序要好很多
当数据有序的时候,while循环的条件总是为假,所以它变成了外层循环中的一个简单语句,执行N-1次
在这种情况下,算法运行至需要N(N)的时间,效率相对来说会更高
另外别忘了,我们的比较次数是选择排序的一半,所以这个算法的效率是高于选择排序的
希尔排序的历史
希尔排序是插入排序的一种高效的改进版,并且效率比插入排序更要快
希尔排序的历史背景:
希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由1959年公布
我们知道,优秀的排序算法首要条件就是速度
在简单排序出现后的很多一段时间内,人们发明了各种各样的算法
但是最终发现算法的时间复杂度都是O(N方),似乎没法超越了
此时,计算机学术界充斥着“排序算法不可能突破O(N方)”的声音
就像之普通认为人类100米短跑不会突破10秒大关一样
终于有一天,一位科学家发布了O(N方)新排序算法(后来为了纪念这个里程碑,用Shell来命名了该算法)
紧接着出现了好几种可以超越O(N方)排序算法,我们后面将的快速排序也是其中之一
所以,所有的限制都是从自己的内心开始的
插入排序的问题
回顾插入排序:
由于希尔排序基于擦汗如排序,所以又必须回顾一下前面的插入排序
我们设想一下,在插入排序执行到一半的时候,标记符左边这部分数据项都是排好序的,而标记符右边的数据项是没有排序的
这个时候,取出指向的那个数据项,把它存储在一个临时变量中,接着,从刚刚移除的位置左边第一个单元开始,
每次把有序的数据项向右移动一个单元,直到存储在临时变量中的数据项可以成功插入
插入排序的问题:
假设一个很小的数据项在很靠近右端的位置上,这里本来应该是较大的数据项的位置
把这个小数据项移动到左边的正确位置,所有的中间数据项都必须向右移动一位。
如果每个位置对数据项都进行N次复制,平均下来是移动N/2,N个元素就是N*N/2 = N方/2
所以我们通常认为插入的排序的效果是O(N方)
如果有某种方式,不需要一个个移动所有中间的数据项,就能把较小的数据项移动到左边,
那么这个算法的执行效率就会有很大的改进
希尔排序的思路
比如下面的数字,81,84,11,96,12,35,17,95,28,58,41,75,15
我们先让间隔为5,进行排序 (35, 81), (94, 17), (11, 95), (12, 58), (35, 41),(17, 75),(95, 15)
排序后的新序列,一定可以让数字离自己的正确的位置更近一步
我们再让间隔为3,进行排序 (35, 28, 75, 58, 95), (17, 12, 15, 81), (11, 41, 96, 94)
排序后的新序列,一定可以让数字离自己的正确位置又近了一步
最后,我们让间隔为1,也就是正确的插入排序
这个时候数字都离自己的位置更近,那么需要复制的次数一定会减少很多

希尔原稿的做法
选择合适的增量:
在希尔排序的原稿中,他建议的初始间距是N / 2,简单的把每趟排序分成两半
也就是说,对于N = 100 的数组,增量间隔序列为:50,25,12,6,3,1
这个方法的好处是不需要在开始排序前为找合适的增量而进行任何的计算
Hibbard 增量序列
增量的算法2 ^ k - 1 也就是为1 3 5 7 … 等等
这种增量的最坏复杂度为O(N ^ 3 / 2),猜想的平均复杂度为O(N ^ 5 / 4),目前尚未被证明
Sedgewick增量序列
{1,5,19,41,109,…},该序列中的项或者是 94 ^ i - 9 * 2 ^ i + 1 或者是 4 ^ i - 32 ^ i + 1
这种增量的最坏复杂度为O(N ^ 4 / 3),平均复杂度为O(N ^ 7 / 6),但是均为被证明
希尔排序的效率
希尔排序的效率
希尔排序的效率很增量是有关系的
但是,它的效率证明非常困难,甚至某些增量的效率到目前依然没有被证明出来
但是经过统计,希尔排序使用原始增量,最坏的情况下时间复杂度为O(N方),通常情况下都要好于O(N方)
总之,我们使用希尔排序大多数情况下效率都高于简单排序
这个可以通过统计排序算法的时间来证明
甚至在合适ide增量和某些数量N的情况下,还好好于快速排序
希尔排序代码
// 希尔排序
ArrayList.prototype.shellSort = function() {
// 获取数组的长度
let length = this.array.length
// 初始化的增量(gap -> 间隔/间隙)
let gap = Math.floor(length / 2)
// while循环(gap不断的减小)
while (gap >= 1) {
// 以gap作为间隔,进行分组,对分组进行插入排序
for (let i = gap; i < length; i++) {
let temp = this.array[i]
let j = i
while (this.array[j - gap] > temp && j > gap - 1) {
this.array[j] = this.array[j - gap]
j -= gap
}
// 将j位置的元素赋值temp
this.array[j] = temp
}
// 增量变化 / 2
gap = Math.floor(gap / 2)
}
}
希尔排序的实现
代码解析
代码序号1:获取数组的长度
代码序号2:计算第一次的间隔,我们按照希尔提出的间隔实现
代码序号3:增量不断变小,大于0就继续改变增量
代码序号4:实际上就是实现了插入排序
代码序号4.1:保存临时变量,j位置从i开始,保存该位置的值到变量temp中
代码序号4.1:内层循环,j > gap - 1 并且temp大于 this.array[j - gap],那么就进行复制
代码序号5:每次while循环后都重新计算新的间隔
快速排序的重要性
快速排序几乎可以说目前所有排序算法中,最快的一种排序算法
当然,没有任何一种算法是在任意情况下都是最优的
比如希尔排序确实在某些情况下可能好于快速排序
但是大多数情况下,快速排序还是比较好的选择
快速排序的重要性:
如果有一天你面试的时候,让你写一个排序算法
你可以洋洋洒洒的写出多个排序算法,但是如果其中没有快速排序
那么证明你对排序算法也只是浅尝辄止,并没有深入的研究过
因为快速排序可以说是排序算法中最常见的,无论是C++的STL中,还是Java的SDK中其实都能找打它的影子
快速排序也被列为20世纪十大算法之一
AnyWay,快速排序非常重要
认识快速排序
希尔排序相当于插入排序的升级版,快速排序其实是我们学习过的最慢的冒泡排序的升级版
我们知道冒泡排序需要经过很多次交换,才能在一次循环中,将最大值放在正确的位置
而快速排序可以在一次排序中(其实是递归调用),找出某个元素的正确位置,并且
该元素之后不需要任何移动
快速排序最重要的思想是分而治之
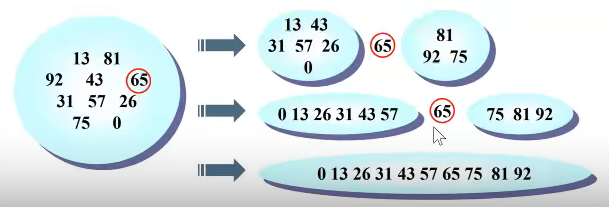
比如我们下面有这样一堆数组需要排序
第一步:从其中选出了65.(其实可以是选出任意的数字,我们以65举个例子)
第二步:我们通过算法:将所有小于65的数组放在65的左边,将所有大于65的数字放在65的右边
第三步:递归的处理左边的数据。(比如问你选择31来处理左侧),递归的处理右边的数据。
(比如选择75来处理右侧,当然选择81可能更合适)
最终:排序完成
和冒泡排序不同的是什么呢?
我们选择的65可以一次性将它放在最正确的位置,之后不需要任何移动
需要从开始位置两个两个比较,如果第一个就是最大值,它需要一直向后移动,直到走到最后
也就是即使已经找到最大值,也需要不断继续移动最大值,而插入排序对数字的定位是一次性的
快速排序的枢纽
在快速排序中有一个很重要的步骤就是选取枢纽(pivot也有人称为主元)
如何选择才是最合适的枢纽呢?
一种方案是直接选择第一个元素为枢纽
但第一个作为枢纽在某种情况下,效率并不是特别高
另一种方案是使用随机数:
随机取pivot?但是随即函数本身就是一个耗性能的操作
另一种比较优秀的解决方案:取头、中、尾的中位数
例如8、12、3的中位数就是8
快速排序的效率
快速排序的最坏情况效率
什么情况下会有最坏的效率呢?就是每次选择的枢纽都是最左边或者最右边的
那么效率等同于冒泡排序
而我们的例子可能有最坏的情况吗?是不可能的。因为我们是选择三个值的中位值
快速排序的平均效率:
快速排序的平均效率是O(N * logN)
虽然其他某些算法的效率也可以达成O(N * logN),但是快速排序是最好的
快速排序完整代码
// 快速排序
// 1. 选择枢纽
ArrayList.prototype.medium = function (left,right) {
// 1. 取出中间的位置
var center = Math.floor((left + right)/2);
// 2. 判断大小,并且进行交换
if ( this.array[left] > this.array[center]){
this.swap(left , center);
};
if (this.array[left] > this.array[right]){
this.swap(left , right);
};
if (this.array[center] > this.array[right]){
this.swap(center , right);
};
// 3.将center换到right-1的位置
this.swap(center , right - 1)
return this.array[right - 1]
};
// 2. 快速排序的实现
ArrayList.prototype.quickSort = function () {
this.quick(0 , this.array.length - 1);
};
ArrayList.prototype.quick= function (left , right) {
// 1. 结束条件
if ( left >= right ){
return
};
// 2. 获取枢纽
var pivot = this.medium(left , right);
// 3. 定义变量,用于当前找到的位置
var i = left;
var j = right - 1;
// 4. 开始进行交换
while (i<j){
while(this.array[++i] < pivot){};
while (this.array[--j] > pivot){};
if (i < j){
this.swap(i , j);
}else{
break;
};
}
// 5. 将枢纽放置在正确的位置,i的位置
this.swap(i ,right-1);
// 6. 分而治之
this.quick(left, i-1);
this.quick(i + 1, right);
};
