数据结构专题-学习笔记：Link Cut Tree 动态树

目录

• 1. 前言
• 2. LCT
  • 2.1 实链剖分
  • 2.2 LCT 存储方式
  • 2.3 基础函数
  • 2.4 Access
  • 2.5 MakeRoot
  • 2.6 FindRoot
  • 2.7 Split
  • 2.8 Link
  • 2.9 Cut
  • 2.10 总体代码
• 3. 参考资料

1. 前言

Link Cut Tree 动态树，简称 LCT，是一种维护动态森林的数据结构。

前置知识：Splay。

2. LCT

例题：P3690 【模板】动态树（Link Cut Tree）

2.1 实链剖分

实链剖分也是一种对树的剖分方式，类似于重链剖分和长链剖分，其将一棵树上的边，随意划分成实边和虚边，每个点到其孩子的所有连边中至多只有一条实边，别的边全都是虚边，即孩子父亲单实边。

注意：实链剖分中我们对边的划分是任意的，并没有任何的限制条件，而且我们可以随时转换实虚边，只要保证一次操作（不是转换）后依然保证孩子父亲单实边即可。

规定：下文中所有图片，实边是实线，虚边是虚线。

实际上 LCT 就是将这棵树划分成若干条实链和虚链，然后将每一条实链用一棵 Splay 维护有关信息，对于每一条实链，Splay 的中序遍历是按照深度递增的点的排列。

（接下来的图都是从 YangZhe 的论文 上找来的）

比如说下面这棵树（被实链剖分之后）：

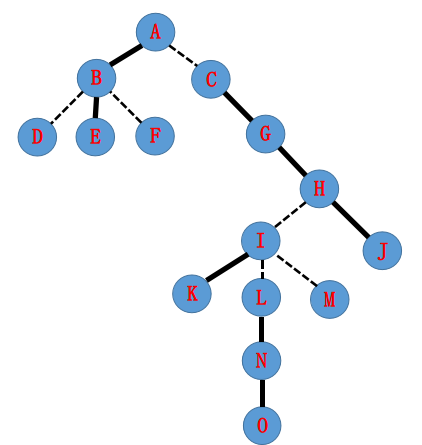
那么这棵树在 LCT 中可能会长这样：

2.2 LCT 存储方式

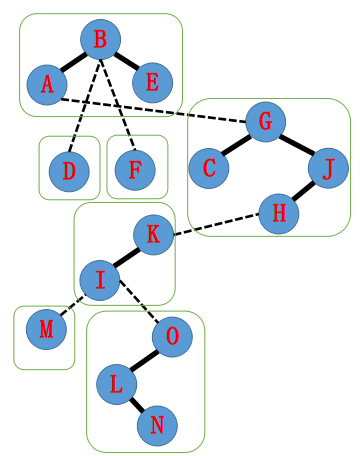
首先 LCT 的存储方式是类似于 Splay 的，需要维护父亲和左右孩子指针。

我们设维护的树根为 R，这样每个点会有一个父亲和左右孩子，对于实边因为在一棵 Splay 里面，因此我们直接正常存储即可，但是对于虚边，我们需要认父不认子，也就是孩子的父亲指针指向父亲，但是父亲并没有指针指向孩子。

比如说还是上图，D 的父亲指针指向 B，但是 B 没有孩子指针指向 D。

据此，我们需要注意，本质上 LCT 是用 Splay 维护树，而认父不认子的虚边连接方式代表这两棵 Splay 在原图中是同一棵树里面的。

根据认父不认子的连边方式，LCT 中我们不能在孩子上用孩子的信息更新父亲，而应该在父亲这里合并两个孩子的信息，因为每个节点存的是自己这棵 Splay 的有关信息。

下文讲解中特别注意区分原树和 LCT 维护的 Splay！

2.3 基础函数

• Connect,Rotate,Splay 函数：就是 Splay 的基础函数，连边，旋转，Splay 到根。
• Update,Spread 函数：更新当前点权值，下传懒标记。
• RightSon 函数：判断两个节点的孩子关系。
• NotRoot 函数：判断一个节点是否是当前 Splay 的根节点，判断方式就是利用认父不认子的连边方式判断。
• PushAll 函数：将当前节点到根节点的所有节点懒标记从上至下下传。

接下来放上结构体和上述函数的代码，特别注意与普通 Splay 不同的地方（有注释）：

struct LCT
{
	int fa, Son[2], val, sum;
	bool tag; // 区间反转懒标记
}spl[MAXN];
#define fa(p) spl[p].fa
#define Son(p, x) spl[p].Son[x]
#define val(p) spl[p].val
#define sum(p) spl[p].sum
#define tag(p) spl[p].tag

void Connect(int f, int s, int id) { fa(s) = f; Son(f, id) = s; }
bool NotRoot(int p) { return Son(fa(p), 0) == p || Son(fa(p), 1) == p; }
bool RightSon(int f, int x) { return Son(f, 1) == x; }
void Update(int p) { sum(p) = sum(Son(p, 0)) ^ val(p) ^ sum(Son(p, 1)); }
void Spread(int p)
{
	if (!tag(p)) return ;
	tag(p) = 0;
	if (Son(p, 0)) { tag(Son(p, 0)) ^= 1; std::swap(Son(Son(p, 0), 0), Son(Son(p, 0), 1)); }
	if (Son(p, 1)) { tag(Son(p, 1)) ^= 1; std::swap(Son(Son(p, 1), 0), Son(Son(p, 1), 1)); }
}
void Rotate(int p)
{
	int f = fa(p), gf = fa(f), id = RightSon(f, p);
	Connect(f, Son(p, id ^ 1), id);
	fa(p) = gf; if (NotRoot(f)) Son(gf, RightSon(gf, f)) = p;
	// 注意！需要判断 f 是不是根节点，如果不是说明 p 和 gf 就不在一个 Splay 里面
	// 此时如果 Son 连边这条边就变成了实边
	Connect(p, f, id ^ 1);
	Update(f); Update(p);
}
void PushAll(int x)
{
	if (NotRoot(x)) PushAll(fa(x));
	Spread(x);
}
void Splay(int p)
{
	PushAll(p); // 实际上普通 Splay 如果涉及懒标记也要 PushAll
	// 这块复杂度正确是因为 p 期望高度为 O(log n)
	while (NotRoot(p))
	{
		int f = fa(p), gf = fa(f);
		if (NotRoot(f))
			if (RightSon(f, p) == RightSon(gf, f)) Rotate(f);
			else Rotate(p);
		Rotate(p);
	}
}

2.4 Access

Access(n) 函数：将当前这个点原图中所在的树（不是 Splay）的根到这个点的路径上的边全部变为实边，放在一棵 Splay 里面，并且根据孩子父亲单实边原则将一些边变成虚边，特别注意 n 节点与其所有孩子的连边全都要是虚边。

如果我们想 Access(N)，那么这棵树应该这样转换：

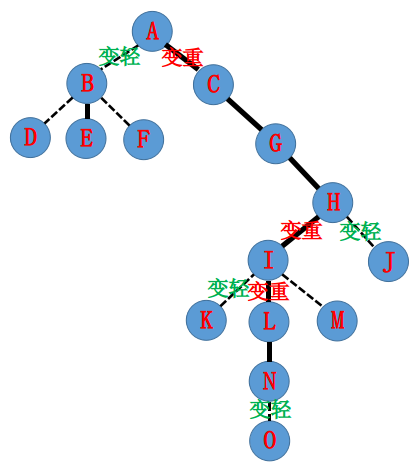
具体步骤如下：

我们设 tmp 表示上一次 Splay 到根的节点，初始 tmp 为 0。

首先将当前操作节点 Splay 到根。

此时这个节点的右孩子原树中深度都是比他大的，将这个节点右孩子置为 tmp，注意这步操作后原先的右儿子和当前节点的边变成了虚边，而上一棵 Splay 的根节点（就是 tmp）与这个点的连边变成了实边，成功完成了实虚边转换。

最后将 tmp 置为当前节点，当前节点跳到其父亲节点，不断重复这些步骤直到当前节点变成根节点。

接下来结合 Access(N) 讲解这些步骤。

首先将 N Splay 到根，然后将 N 右孩子置为 tmp，tmp 置为 N：

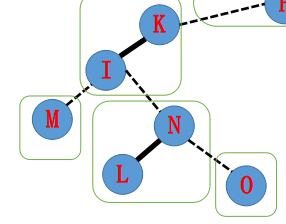
当前指针指向 I，将 I Splay 到根，右孩子置为 tmp = N，tmp 置为 I：

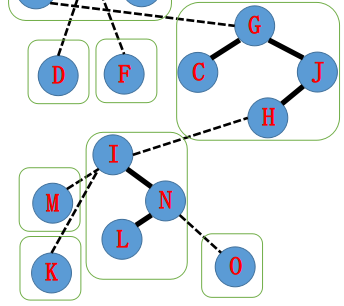
当前指针指向 H，将 H Splay 到根，右孩子置为 tmp = I，tmp 置为 H：

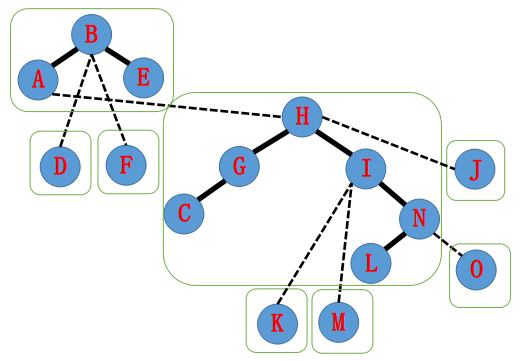
当前指针指向 A，将 A Splay 到根，右孩子置为 tmp = H，tmp 置为 A：

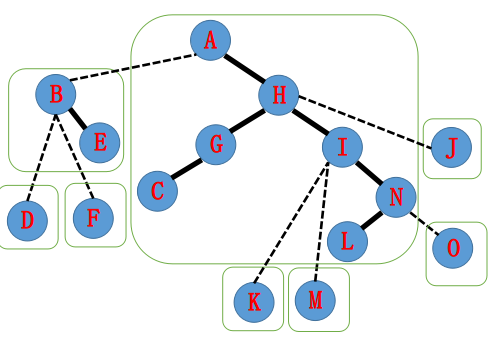
注意到当前指针已经是根节点了，结束 Access 操作，成功达到了我们的目的。

Code：

void Access(int p)
{
	for (int x = 0; p; x = p, p = fa(p))
	// 这里判的是原树树根，所以不要用 NotRoot(p)
	{
		Splay(p); Son(p, 1) = x; Update(p);
	}
}

2.5 MakeRoot

MakeRoot(p) 函数：将 p 节点换成当前根节点。

首先 Access(p)，这样根节点到 p 节点的所有点在一棵 Splay 里面并且没有别的点，然后 Splay(p) 使其变成当前 Splay 的根节点。

因为 p 是没有右孩子的（深度最大），而根节点要求深度最小，因此我们直接反转整棵 Splay，就可以将 p 置为原树的根（深度变成了最小），这也就是反转懒标记的用处。

实际上如果原先的根为 R，那么 R 到 p 上的所有点的父亲孩子关系会改变，深度相对大小也会随之改变，但是在路径之外的点相对深度和父亲孩子关系没有改变，因此这样操作是正确的。

MakeRoot 之后根节点就是 p 并且其没有左孩子。

Code：

void MakeRoot(int p)
{
	Access(p); Splay(p); tag(p) ^= 1; std::swap(Son(p, 0), Son(p, 1));
}

2.6 FindRoot

FindRoot(p) 函数：找到 p 所在树的树根。

首先还是要 Access(p) 并且 Splay(p)，这两步和 MakeRoot 是一样的。

由于根节点深度最小，因此我们在 p 所在的 Splay 中直接找出深度最小的点也就是一直往左孩子走，注意下传懒标记。

最后由于要保证复杂度，我们还需要将树根 Splay 到根节点，这个的原理就是参考 Splay 操作时的一条铁律：所有被操作或查询的点最后都需要 Splay 到根，否则不能保证复杂度。

Code：

int FindRoot(int p)
{
	Access(p); Splay(p);
	while (Son(p, 0)) { Spread(p); p = Son(p, 0); }
	// 注意下传懒标记
	Splay(p); return p;
}

2.7 Split

Split(x, y)：将 x -> y 的路径拉出来成为一条实链并且用一个 Splay 维护。

首先换根，MakeRoot(x)，然后再 Access(y)，这样就成功的将这条链拉出来了。

同样的为了保证复杂度，我们还是要 Splay(y)，然后你要查询的东西就都在 y 上了。

Code：

void Split(int x, int y)
{
	MakeRoot(x); Access(y); Splay(y);
}

2.8 Link

Link(x, y)：连边 x,y，注意判定非法情况。

由于 LCT 维护的是森林，因此需要注意连边是否成环。

首先 MakeRoot(x)，然后我们 FindRoot(y)，如果找出来的根就是 x 说明这两个点已经在一棵树上了，连边非法不能连，否则就令 fa(x) = y 认父不认子连虚边。

Code：

void Link(int x, int y)
{
	MakeRoot(x); if (FindRoot(y) == x) return ;
	fa(x) = y;
}

2.9 Cut

Cut(x, y)：将 x,y 的连边断掉，注意判定非法情况。

这里断掉的边就是 x,y 间的直接连边，因此要断需要满足 x,y 的深度值相差一并且两者存在父亲关系（不是父子）

首先 MakeRoot(x)，然后需要满足：y 的父亲是 x 并且 x 有一个孩子是 y。

如果希望判定 x 有一个孩子是 y 最直接的方式就是 x,y 这条边为实边，但实际情况并不一定。

因此首先 FindRoot(y)，如果结果不是 x 显然不能断边，但因为 FindRoot(y) 中有一步是 Access(y)，说明此时 x -> y 一定在一棵 Splay 内，这个时候就可以判定了，非法情况是 fa(y) 不是 x 或者 y 有左孩子（说明 x,y 深度差不是 1）。

Code：

void Cut(int x, int y)
{
	MakeRoot(x);
	if (FindRoot(y) != x || fa(y) != x || Son(y, 0)) return ;
	fa(y) = 0; Son(x, 1) = 0; Update(x);
}

2.10 总体代码

GitHub：CodeBase-of-Plozia

下面是模板题的总代码：

/*
========= Plozia =========
	Author:Plozia
	Problem:P3690 【模板】动态树（Link Cut Tree）
	Date:2022/4/12
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 1e5 + 5;
int n, q;
struct LCT
{
	int fa, Son[2], val, sum;
	bool tag; // 区间反转懒标记
}spl[MAXN];
#define fa(p) spl[p].fa
#define Son(p, x) spl[p].Son[x]
#define val(p) spl[p].val
#define sum(p) spl[p].sum
#define tag(p) spl[p].tag

int Read()
{
	int sum = 0, fh = 1; char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = sum * 10 + (ch ^ 48);
	return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }

void Connect(int f, int s, int id) { fa(s) = f; Son(f, id) = s; }
bool NotRoot(int p) { return Son(fa(p), 0) == p || Son(fa(p), 1) == p; }
bool RightSon(int f, int x) { return Son(f, 1) == x; }
void Update(int p) { sum(p) = sum(Son(p, 0)) ^ val(p) ^ sum(Son(p, 1)); }
void Spread(int p)
{
	if (!tag(p)) return ;
	tag(p) = 0;
	if (Son(p, 0)) { tag(Son(p, 0)) ^= 1; std::swap(Son(Son(p, 0), 0), Son(Son(p, 0), 1)); }
	if (Son(p, 1)) { tag(Son(p, 1)) ^= 1; std::swap(Son(Son(p, 1), 0), Son(Son(p, 1), 1)); }
}
void Rotate(int p)
{
	int f = fa(p), gf = fa(f), id = RightSon(f, p);
	Connect(f, Son(p, id ^ 1), id);
	fa(p) = gf; if (NotRoot(f)) Son(gf, RightSon(gf, f)) = p;
	// 注意！需要判断 f 是不是根节点，如果不是说明 p 和 gf 就不在一个 Splay 里面
	// 此时如果 Son 连边这条边就变成了实边
	Connect(p, f, id ^ 1);
	Update(f); Update(p);
}
void PushAll(int x)
{
	if (NotRoot(x)) PushAll(fa(x));
	Spread(x);
}
void Splay(int p)
{
	PushAll(p); // 实际上普通 Splay 如果涉及懒标记也要 PushAll
	// 这块复杂度正确是因为 p 期望高度为 O(log n)
	while (NotRoot(p))
	{
		int f = fa(p), gf = fa(f);
		if (NotRoot(f))
			if (RightSon(f, p) == RightSon(gf, f)) Rotate(f);
			else Rotate(p);
		Rotate(p);
	}
}
void Access(int p)
{
	for (int x = 0; p; x = p, p = fa(p))
	// 这里判的是原树树根，所以不要用 NotRoot(p)
	{
		Splay(p); Son(p, 1) = x; Update(p);
	}
}
void MakeRoot(int p)
{
	Access(p); Splay(p); tag(p) ^= 1; std::swap(Son(p, 0), Son(p, 1));
}
int FindRoot(int p)
{
	Access(p); Splay(p);
	while (Son(p, 0)) { Spread(p); p = Son(p, 0); }
	// 注意下传懒标记
	Splay(p); return p;
}

void Split(int x, int y)
{
	MakeRoot(x); Access(y); Splay(y);
}

void Link(int x, int y)
{
	MakeRoot(x); if (FindRoot(y) == x) return ;
	fa(x) = y;
}

void Cut(int x, int y)
{
	MakeRoot(x);
	if (FindRoot(y) != x || fa(y) != x || Son(y, 0)) return ;
	fa(y) = 0; Son(x, 1) = 0; Update(x);
}

int main()
{
	n = Read(), q = Read();
	for (int i = 1; i <= n; ++i) val(i) = Read();
	while (q--)
	{
		int opt = Read(), x = Read(), y = Read();
		if (opt == 0) { Split(x, y); printf("%d\n", sum(y)); }
		if (opt == 1) { Link(x, y); }
		if (opt == 2) { Cut(x, y); }
		if (opt == 3) { Splay(x); val(x) = y; Update(x); }
	}
	return 0;
}

3. 参考资料

• LCT总结——概念篇+洛谷P3690[模板]Link Cut Tree(动态树)（LCT，Splay） - Flash_Hu - 自由互联
• 【AgOHの算法胡扯】Link/Cut Tree_哔哩哔哩_bilibili