[Unity] 基础寻路算法 - 代码实践

本文始发于：https://www.cnblogs.com/wildmelon/p/16159189.html

一、前言

本文为常见的以图作为数据结构的寻路算法笔记，再次推荐该文章：
https://www.redblobgames.com/pathfinding/a-star/introduction.html
既有可交互的可视化界面，又有由浅到深的寻路算法讲解。

二、广度优先搜索(BFS)

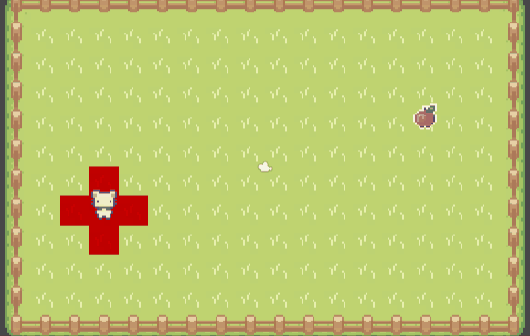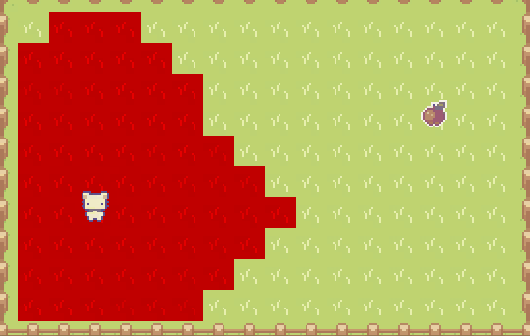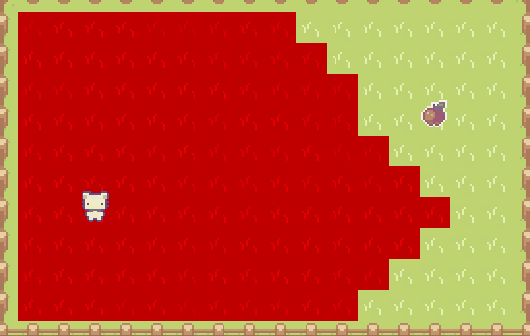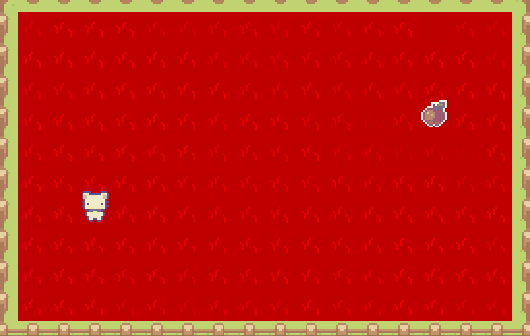
广度优先搜索的循环，是所有寻路算法（基于图节点）的关键。实际上会从起点开始，像在 Minecraft 游戏里倒一桶水般蔓延开来，遍历到图中的每个节点：

// 待搜索队列
Queue<TileNode> frontier = new Queue<TileNode>();
// 已搜索节点
HashSet<TileNode> reached = new HashSet<TileNode>();
// 从起点开始
TileNode start = TotalTileModels[character.cellPosition];
frontier.Enqueue(start);
reached.Add(start);
// 遍历搜索上下左右的邻节点
while (frontier.Count != 0)
{
    TileNode current = frontier.Dequeue();
    foreach (TileNode neighbor in current.neighbors)
    {
        if (!reached.Contains(neighbor))
        {
            frontier.Enqueue(neighbor);
            reached.Add(neighbor);
        }
    }
}

如果需要找到路径，则用字典记录每个节点的“父节点”，找到目的地之后，从尾节点向上返回到起点：

private void BFS()
{
    Queue<TileNode> frontier = new Queue<TileNode>();
    // 若 cameFrom[B]=A，说明B的上一节点为A，B是在A的邻居中找到的
    Dictionary<TileNode, TileNode> cameFrom = new Dictionary<TileNode, TileNode>();
    TileNode start = TotalTileModels[character.cellPosition];
    TileNode target = TotalTileModels[destination.cellPosition];
    frontier.Enqueue(start);
    cameFrom.Add(start, null);
    while (frontier.Count != 0)
    {
        TileNode current = frontier.Dequeue();
        foreach (TileNode neighbor in current.neighbors)
        {
            if (!cameFrom.ContainsKey(neighbor))
            {
                frontier.Enqueue(neighbor);
                cameFrom.Add(neighbor, current);
                // 找到目标，提前退出
                if (neighbor == target) break;
            }
        }
    }
    TileNode link = target;
    while (cameFrom[link] != null)
    {
        path.Add(link);
        link = cameFrom[link];
    }
    path.reverse();
}

如果 path 为空，即字典 cameFrom 不存在 target。则说明没有从终点返回起点的路径。

三、Dijkstra 算法

广度优先搜索对于所有的节点采取一视同仁的态度，但许多游戏都存在地形的概念，如沙漠、森林等地点可能会消耗更多的步行时间。

此时我们引入成本记录跟踪，来得到 Dijkstra 算法，为了在待搜索节点中先计算当前成本最低的节点，需使用优先级队列：

private void Dijkstra()
{
    // 优先级队列
    PriorityQueue frontier = new PriorityQueue();
    Dictionary<TileNode, TileNode> cameFrom = new Dictionary<TileNode, TileNode>();
    // 当前节点已消耗的成本
    Dictionary<TileNode, int> costSoFar = new Dictionary<TileNode, int>();

    TileNode start = TotalTileModels[character.cellPosition];
    TileNode target = TotalTileModels[destination.cellPosition];
    // 从起点开始搜索
    frontier.Push(start, 0);
    costSoFar.Add(start, 0);
    cameFrom.Add(start, null);

    while (frontier.GetCount() != 0)
    {
        TileNode current = (TileNode)frontier.Out();
        // 到达目标，提前退出
        if (current == target) break;
        foreach (TileNode neighbor in current.neighbors)
        {
            int newCost = costSoFar[current] + neighbor.cost;
            // 未计算过该节点，或有新成本更低的路径时，才进行计算
            if (!costSoFar.ContainsKey(neighbor) || newCost < costSoFar[neighbor])
            {
                frontier.Push(neighbor, newCost);
                costSoFar[neighbor] = newCost;
                cameFrom.Add(neighbor, current);
                mClickableTilemap.mTilemap.SetColor(neighbor.position, Color.blue);
            }
        }
    }
    while (cameFrom[target] != null)
    {
        mClickableTilemap.mTilemap.SetColor(target.position, Color.red);
        target = cameFrom[target];
    }
}

Dijkstra 算法，会跳过中间消耗更高的水路：

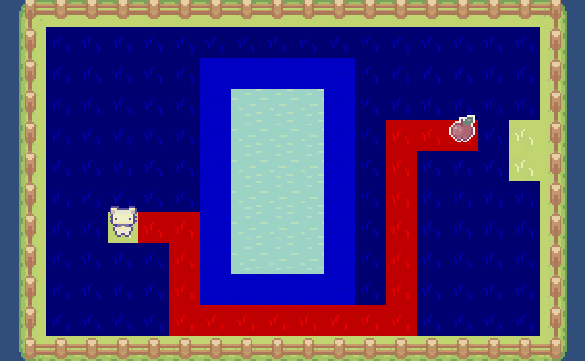
同时可以发现，如果每个地块的移动成本都是一致的（比如都是平原），那么 Dijkstra 算法和广度优先搜索其实是一样的。

四、启发式函数（Heuristic function）

无论是广度优先搜索还是 Dijkstra 算法，都是以一种往外辐射的方式进行扩散的。但路径寻找通常是有明确的方向性的（从起点指向终点方向），Dijkstra 算法会往相反的方向扩散，对性能造成较大影响。

Dijkstra 算法，只记录了从起点到当前点的已消耗成本。我们将定义一个启发式函数，对距离目标还有多远进行评估，来得到（预估成本）。

某个节点的总成本=已消耗成本+预估成本，在待搜索队列中，优先选取总成本最低的节点进行计算。

预估成本可以由距离、时间或者其他游戏特定因素来决定的。

以距离为例，常用的启发式函数有两种：

1. 曼哈顿距离：h(node) = |node.x-target.x| + |node.y-target.y|
2. 欧几里得距离：h(x) = sqrt(pow(node.x-target.x, 2) + pow(node.y-target.y, 2))

理想情况下，启发式结果与真实结果越相近越好，上面两个距离相关的启发式函数，在节点离终点越近时，预估成本都越小。

举例来说，同样是一片平原，已消耗成本为6时，有多种方案可选，既可以往终点走6步，也可以远离终点。而在加入了启发式函数进行预估成本评估后，显然离终点更近的节点的预估成本和总成本会更低，并优先选取计算。

“曼哈顿距离”的预估成本通常会高于真实开销，因为可能存在对角线斜走的可能，有一定概率无法发现最佳路径。

“欧几里得距离（两点之间的直线距离）”的预估成本通常低于真实开销，则可能会遍历更多的节点影响性能。

五、贪婪最佳优先算法

在贪婪最佳优先算法中，会忽略已消耗成本，只考虑启发函数计算的预估成本。
即：某个节点的总成本=预估成本。

以“曼哈顿距离”为启发式函数为例，贪婪最佳优先算法会优先考虑离目标更近的点：

private void Greedy()
{
    PriorityQueue frontier = new PriorityQueue();
    Dictionary<TileNode, TileNode> cameFrom = new Dictionary<TileNode, TileNode>();

    TileNode start = TotalTileModels[character.cellPosition];
    TileNode target = TotalTileModels[destination.cellPosition];

    frontier.Push(start, 0);
    cameFrom.Add(start, null);

    while (frontier.GetCount() != 0)
    {
        TileNode current = (TileNode)frontier.Out();
        // 到达目标，提前退出
        if (current == target) break;
        foreach (TileNode neighbor in current.neighbors)
        {
            if (neighbor.nodeType == NodeType.Road && !cameFrom.ContainsKey(neighbor))
            {
                int cost = heuristic(neighbor, target);
                frontier.Push(neighbor, cost);
                cameFrom.Add(neighbor, current);
                mClickableTilemap.mTilemap.SetColor(neighbor.position, Color.blue);
            }
        }
    }
    while (cameFrom[target] != null)
    {
        mClickableTilemap.mTilemap.SetColor(target.position, Color.red);
        target = cameFrom[target];
    }
}

在平坦地形上，贪婪算法效率是很高的，因为他会直奔目标而去（优先考虑预估距离更近的点）。但当存在障碍物时，路径质量可能不太理想，因为会一直先取更近的点，所以可能会得到不太准确的路径：

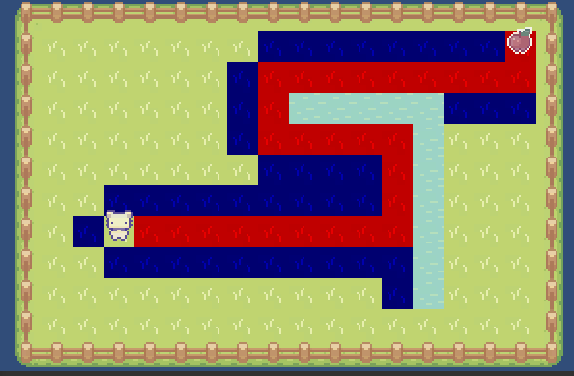
如图，起点左边、上边、下方的方块由于距离更远的原因，会排在优先级队列的尾部，起点右上方的方块会优先计算并组成路径。

六、A* 算法

上文可知：
对于 Dijkstra 算法，总成本=已消耗成本，可以很好地找到最短路径，但在方向不确定的情况下会消耗更多的性能。

对于贪婪最佳优先算法，总成本=预估成本，效率更高，但可能找不到最短路径。

而 A* 算法，综合了考虑当下和未来（由启发式函数决定）：总成本=已消耗成本+预估成本。

// 微调 Dijkstra 函数即可
...
int priority = newCost + heuristic(neighbor, target);
frontier.Push(neighbor, priority);
...

由上代码可知，Dijkstra 算法可当作 heuristic 函数返回 0 的A*算法。

七、总结

三种算法是在“已消耗成本”与“预估成本”之间进行评估，以在效率和路径质量之间做取舍。

本质上仍旧是开头的“广度优先搜索”循环的一种优化。

可视化对比三种算法的不同，可参考 redblobgames 的这篇文章末尾：https://www.redblobgames.com/pathfinding/a-star/introduction.html