整数 整除今天开始,系统学习庄金成老师讲授的《公钥密码学数学基础(上)》
需要用到两个数学工具:NTL 和 sage
B%A=0,就是B除A没有余数,B可以被A整除,或者A整除于B,记\(A|B\),B是A的倍数,A是B的除数(约数、因子)
这里整除的几何意义,举一个现实的例子"A刚好能丈量B":

性质:

素数一般我们只取正的
假设\(b(b\neq 0,1)\)是一个整数,除了1和自身b之外,没有其他因子,那么b就叫做不可约数(素数、质数)。
性质1和b叫做显然因子;其他因子叫做非显然因子(真因子)
合数就是和素数相反,除了1和自身之外还有其他因子的数
(1)若a为合数,则a的最小真因子为素数

(2)素数有无穷个

定理源于《几何原本》
(3)素数的初等估计:记\(p_n\)是第n个素数,\(\pi (x)\)表示不超过x的素数个数,将全体素数按从小到大排序,有以下性质:
- \[p_n \leqslant 2^{2^{n-1}},n=1,2,... \]

- \[\pi(x)>log_2log_2x,x\geqslant 2 \]

RSA加密算法中的密钥生成,需要生成两个素数:

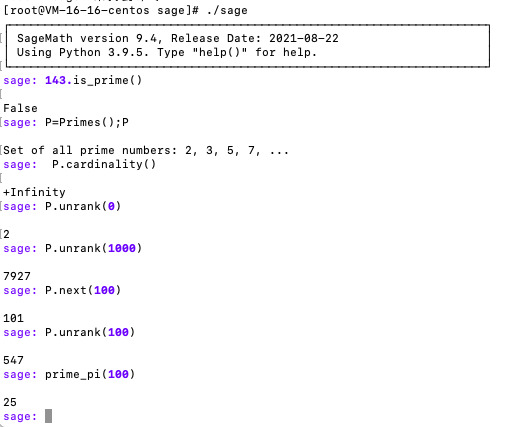
点击查看代码
sage: 143.is_prime() //检测143是否为素数
False
sage: P=Primes();P //定义P是素数集合,无穷多个素数
Set of all prime numbers: 2, 3, 5, 7, ...
sage: P.cardinality() //返回P集合的大小,为无穷大
+Infinity
sage: P.unrank(0) //返回P集合中的第几个素数
2
sage: P.unrank(1000)
7927
sage: P.next(100) //返回P集合中100的下一个素数
101
sage: prime_pi(100) //不超过100的素数个数
25
- 素数分布比较好的估计素数定理:$\pi(x)=x/lnx,x->\infty $
- 更精细的估计:黎曼假设
- 未解决的素数问题:哥德巴赫猜想,孪生素数猜想等
设a,b是两个给定的整数且\(a\neq 0\),则一定存在唯一的一对整数q和r,满足:
\[b=qa+r,0\leqslant r\leqslant |a| \]其中r叫做b被a除后的最小非负余数
证明整除时,r=0;令a=7,b=12
12=17+5,5就是最小正剩余;12=27-2,-2就是最小绝对剩余


CRT:

整数分类详细证明见"孙子定理"
通过给定a,可以将r分类
给定正整数\(a\geqslant 2\),\(j=0,1,2,..,a-1\),对于给定的j,被a除后余数等于j的全体整数是
\[ak+j,k=0,\pm 1,\pm 2,... \]这些整数组成的集合记\(S_{a,j}\)。就是下面介绍的剩余类

性质
分类\(S_{a,j}\):\(0\leqslant j\leqslant a-1\)下:
- \(S_{a,j}\)中任何两个不相交,即
- \(S_{a,j}\)中所有集合的并等于\(Z\),即
例子:在表盘中,12个刻度代表集合的不相交
应用(1)对于任意整数x,\(x^3\)被9除后所得的最小负余数是0,1,8

(2)进制表示

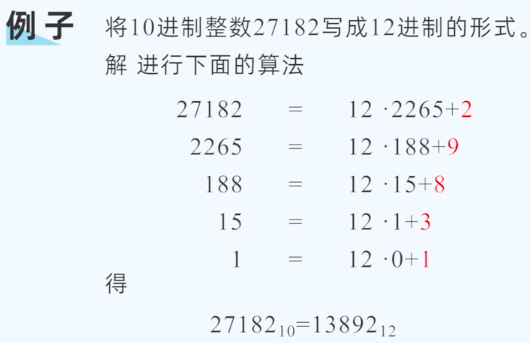
参考:最大公约数&最小公倍数
公因子:
若d|a,d|b,则d是a和b的公因子。
若d是a和b的正公因子,对于任意的公因子d‘,有d'|a,d'|b,d'|d,则d是a和b的最大公因子,即gcd(a,b)=d。
性质:

求最大公因子的方法:
(1)辗转相除法(欧几里得算法)
(2)更相减损术(《九章算术》)

若1=gcd(a,b),则称a和b是互素的(或者叫既约的)
性质:




性质:
(1)任意两个不同的费马数互素
(2)\(F_m=\prod_{i=0}^{m-1}F_i+2\)
点击查看代码
sage: def Fermat(n): //定义费马数函数
....: return 2^(2^n)+1
....:
sage: for i in range(5): //一次返回前0-4个费马数,且判断是否为素数
....: print(Fermat(i),Fermat(i).is_prime())
....:
3 True
5 True
17 True
257 True
65537 True
sage: print(Fermat(5),Fermat(5).is_prime()) //返回第5个费马数且判断是否为素数
4294967297 False

举例:

以上证明来自"毕达哥拉斯"
公倍数:
若a|d,b|d,则d是a和b的公倍数。
若d是a和b的一个大于0的公倍数,对于a和b的其他任意公倍数d‘,有d|d'。则d是a和b的最小公倍数。记d=[a,b]
性质:
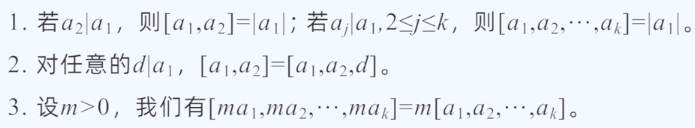

求最小公倍数的方法:

又叫做辗转相除法,用于求最大公因子


算法上述算法,余数取得非负最小剩余的欧几里得算法,也可以采用绝对最小剩余(非负最小的就是非负的还是最小的哪一个;绝对最小就是绝对值最小的那一个)
非负最小剩余:
设a,b是两个整数,其中b>0,则存在两个唯一的整数q及r,使得a=bq+r,0≤r<b成立,我们把式中的q叫做a被b除得的不完全商,r叫做a被b除所得的余数,也叫做非负最小剩余。
绝对最小剩余:
设a,b是两个整数,其中b>0,则存在两个唯一的整数q及r,使得a=bq+r,-b/2≤r<b/时成立,我们把式中的q叫做a被b除得的不完全商,r叫做a被b除所得的余数,也叫做绝对最小剩余。




这也是一种求逆的方法



举例:
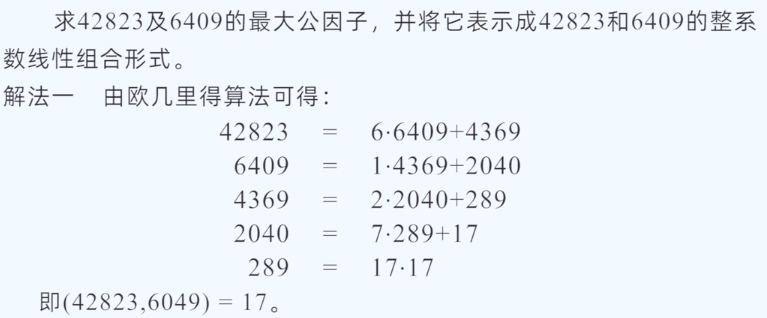

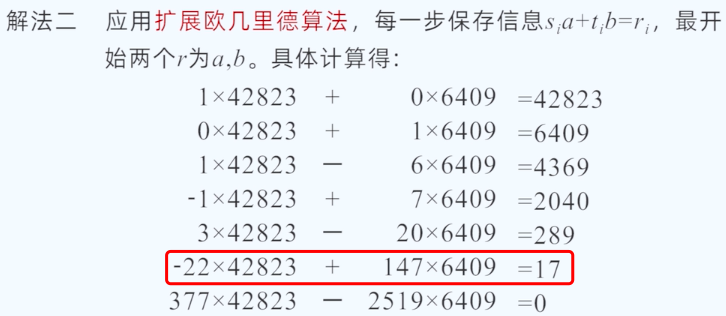
方法2,使用扩展欧几里德算法
具体:先写出前两行;第三行=第一行减去第二行的"6倍";第四行=第二行减去第三行的"一倍";依次继续。(注意这个倍数是怎么来的)
RSA算法分析:

问题:如何计算d使得 \(ed+d'\psi(N) =1\)?
方法(1):扩展欧几里德算法
方法(2):大衍求一术(秦九韶-《数学九章》)
RSA算法的破解:

点击查看代码
sage: gcd(428344,4421412) //求两个数的最大公因子
4
sage: xgcd(324353452314,654634253142) //求两个数的最大公因子,并且返回最大公因子关于两个数的整系数表示
(6, -6798771628, 3368606269)
sage: -6798771628*324353452314+3368606269*654634253142 //验证
6


变元个数多于方程个数,且取整数值的方程(或方程组)成为不定方程(或不定方程组)
不定方程也叫做丢番图方程,研究的基本问题是:
(1)判断何时有解
(2)有解时决定解的个数
(3)求出所有的解
(1)无解

(2)有解


求解:


求解:


先引入素数的一个性质:

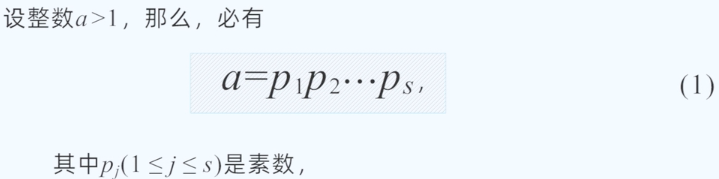
算法基本定理保证了素分解的存在性和唯一性。
举例:

给定正整数N,求解素因子(素因子:是素数的因子);该问题一般情况下是计算困难的。(RSA中)
举例:

sage实验:
点击查看代码
sage: factor(123456789) //分解123456789=3^2 * 3607 * 3803
3^2 * 3607 * 3803
推论:
推论1:

光滑性:
若正整数a的素因子都是不超过b的,则称a是b光滑的。
举例:123456789=3^2 * 3607 * 3803,称123456789是3803光滑的
推论2:

推论3:

推论4:
(a,[b,c])=[(a,b),(a,c)]
推论5:

推论6:

列出所有小于或等于正整数n的素数

代码:
点击查看代码
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 1000
int main()
{
//定义两个变量i,j,一个数组a[N]
int i, j, a[N];
//将数组初始化为1,a[i] = 1表示i为素数
//初始时默认从2到N-1均为素数
for(i = 2; i < N; i++ )
{
a[i] = 1;
}
//遍历数组找出下标为素数的,并将所有下标为该素数的倍数的值改为0
for(i = 2; i < N; i++)
{
if(a[i])
{
for(j = i; i*j < N; j++)
{
a[i*j] = 0;
}
}
}
//输出2~N范围内的素数
for(i = 2; i < N; i++)
{
if(a[i])
{
printf("%4d", i);
}
}
return 0;
}
主要针对\(n!的素分解\):不超过n的素因子p都会出现在分解式中,问题是出现了多少次(求解方幂)
整数函数和小数函数\([x]\)表示x的整数部分;\(x-[x]\)表示x的小数部分
性质:



这里的\(\alpha\)表示p在\(n!\)的素分解中出现的次数

表示\(n!=p_1^{\alpha(p_1,n)}.p_2^{\alpha(p_2,n)}....p_n^{\alpha(p_n,n)}\)
例子:

这里求5的次幂,目的是为了求10的幂次,因为,根据公式( \(10^k = 2^k . 5^k\)),2的幂次比5的高(素数越小,则对应的次幂就越大),因此10的幂次等于5的幂次。



