String.hashCode()为什么使用31作为乘数【深度长文】

String.hashCode()为什么使用31作为乘数

@

目录

• String.hashCode()为什么使用31作为乘数
  • String.hashCode()源码
  • 散列函数
  • 散列表
  • 《Effective Java》上的回答
    • 为什么要选择奇数
    • 为什么要选择素数
      • 1. 取模
      • 2. 选取数列
      • 3. 验证
      • 4. 结论
      • 举例
      • 数学证明
    • 为什么要选择31
      • 源码
      • 存在的问题
      • 解决方案
      • 几种候选乘数的比较
      • 小结
  • 理想的哈希函数
    • 公式推导
    • 公式应用
    • String.hashCode()的目的
  • 总结

String.hashCode()源码

公式：\(H(key) = key\ mod \ p\)

源码：

public int hashCode() {
    int h = hash;
    if (h == 0 && value.length > 0) {
        char val[] = value;
        for (int i = 0; i < value.length; i++) {
            h = 31 * h + val[i];
        }
        hash = h;
    }
    return h;
}

在获取hashCode的源码中可以看到，有一个固定值31，在for循环每次执行时进行乘积计算，循环后的公式如下；s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]

这里的乘数也就是公式中的模/除数，那么为什么这里是31呢？我们先来看看散列函数和散列表的性质。

 

散列函数

所有散列函数都有如下一个基本特性：如果两个散列值是不相同的（根据同一函数），那么这两个散列值的原始输入也是不相同的。

https://zh.wikipedia.org/wiki/%E6%95%A3%E5%88%97%E5%87%BD%E6%95%B8

所以我们在重写equals()方法时同时要重写HashCode()方法。

 

散列表

散列表是散列函数的一个主要应用，使用散列表能够快速的按照关键字查找数据记录。（注意：关键字不是像在加密中所使用的那样是秘密的，但它们都是用来“解锁”或者访问数据的）。

举个英文字典的例子，开头相同字母对应多个单词，相同字母越多（规则越严格），匹配结果越少（冲突越少）。

一个好的散列函数具有均匀的真正随机输出，因而平均只需要一两次探测（依赖于装填因子）就能找到目标。同样重要的是，随机散列函数不太会出现非常高的冲突率。但是，少量的可以估计的冲突在实际状况下是不可避免的（参考生日悖论或鸽巢原理）。

在概率论中，生日问题要求在一组n个随机选择的人中，至少有两个人共享一个生日的概率。生日悖论是，与直觉相反，在一个只有 23 人的小组中，共享生日的概率超过 50% 。
 
虽然只需要 23 个人才能达到 50% 的共享生日概率似乎令人惊讶，但考虑到将在每对可能的个人之间进行生日比较，这一结果变得更加直观：对于 23 个人，需要考虑 (23 × 22) / 2 = 253 对，这远远超过一年中天数（182.5 或 183）的一半。
 
生日悖论普遍应用于检测哈希函数：N位长度的哈希表可能发生碰撞测试次数不是 \(2^N\) 次而是\(2^{N-1}\)次。
 
https://en.wikipedia.org/wiki/Birthday_problem

鸽巢原理经常在计算机领域得到真正的应用。比如：哈希表的重复问题（冲突）是不可避免的，因为Keys的数目总是比Indices的数目多，不管是多么高明的算法都不可能解决这个问题。
 
https://zh.wikipedia.org/wiki/%E9%B4%BF%E5%B7%A2%E5%8E%9F%E7%90%86

 

《Effective Java》上的回答

之所以选择31，是因为它是一个奇素数。如果乘数是偶数，并且乘法溢出的话，信息就会丢失，因为与2相乘等价于移位运算。
 
使用素数的好处并不很明显，但是习惯上都使用素数来计算散列结果。
 
31有个很好的特性，即用移位和减法来代替乘法，可以得到更好的性能：31 * i ==（i << 5）- i。现代的VM可以自动完成这种优化。

https://stackoverflow.com/questions/299304/why-does-javas-hashcode-in-string-use-31-as-a-multiplier

这是个比较有争议的答案，分为三部分来讨论：
 

为什么要选择奇数

如果用2作乘数，则所有的数会落在0和1两个位置（余0或余1）。

2不能作为乘数，则剩下的素数肯定是奇数。问题就转换为为什么要选择素数。
 

为什么要选择素数

实践角度：

1. 取模

取6和7为候选乘数，6的因子集合为{1，2，3，6}，7的因子集合为{1，7}
 

2. 选取数列

数列的选取很重要，有些文章将验证的数列间隔选为1，发现素数与合数并没有什么区别。

这是因为素数与合数最大的区别不是间隔为1，而是因子的个数，我们可以做这样的一个假设，取模运算产生的碰撞冲突与乘数的因子相关。
 

3. 验证

{1，3，5，7，9，11，13，15，17}，取模6

余数 0 1 2 3 4 5 哈希表 1 3 5 冲突1 7 9 11 冲突2 13 15 17

数列间隔为2，2是6的因子。

冲突较多，取模结果分布不均匀，0，2，4未存储，1，3，5冲突很多。

{1，3，5，7，9，11，13，15，17}，取模7

余数 0 1 2 3 4 哈希表 7 1 9 3 11 冲突1 15 17

数列间隔为2，不是7的因子。

冲突较少，取模结果分布均匀

---

{2，4，6，8，10，12，14，16，18}，取模6

余数 0 1 2 3 4 哈希表 6 2 4 冲突1 12 8 10 冲突2 18 14 16

数列间隔为2，2是6的因子。

冲突较多，取模结果分布不均匀。

{2，4，6，8，10，12，14，16，18}，取模7

余数 0 1 2 3 4 哈希表 14 8 2 10 4 冲突1 16 18

数列间隔为2，不是7的因子。

冲突较少，取模结果分布均匀

---

{1，4，7，10，13，16，19，22，25，28}，取模6

余数 0 1 2 3 4 哈希表 1 4 冲突1 7 10 冲突2 13 16 冲突3 19 22 冲突4 25 28

数列间隔为3，3是6的因子。

冲突较多，取模结果分布不均匀。

{1，4，7，10，13，16，19，22，25，28}，取模7

余数 0 1 2 3 4 5 6 哈希表 7 1 16 10 4 19 13 冲突1 28 22 25

数列间隔为3，不是7的因子。

冲突较少，取模结果分布均匀

---

{1，7，13，19，25，31，37，43，49}，取模6

余数 0 1 2 3 4 哈希表 1 冲突1 7 冲突2 13 冲突3 19 冲突4 25 冲突5 31 冲突6 37 冲突7 43 冲突8 49

数列间隔为6，6是6的因子。

冲突较多，取模结果分布不均匀。

{1，7，13，19，25，31，37，43，49}，取模7

余数 0 1 2 3 4 哈希表 7 1 37 31 25 冲突1 49 43

数列间隔为6，不是7的因子。

冲突较少，取模结果分布均匀

---

{1，8，15，22，29，36，43，50，57}，取模6

余数 0 1 2 3 4 哈希表 36 1 8 15 22 冲突1 43 50 57

数列间隔为7，不是6的因子。

冲突较少，取模结果分布均匀

{1，8，15，22，29，36，43，50，57}，取模7

余数 0 1 2 3 哈希表 1 冲突1 8 冲突2 15 冲突3 22 冲突4 29 冲突5 36 冲突6 43 冲突7 50 冲突8 57 4. 结论

• 如果有一个数列s，间隔为1，那么不管模数为几，都是均匀分布的，因为间隔为1是最小单位

• 如果一个数列s，间隔为模本身，那么在哈希表中的分布仅占有其中的一列，也就是处处冲突

• 数列的冲突分布间隔为因子大小，同样的随机数列，因子越多，冲突的可能性就越大

通过上面的分析，答案就很明确了。
 
如果给我们随机的数列放到哈希表中，如何保障它能尽量减少冲突呢，就需要模的因子最少，而因子最少的就是素数，这就是哈希表取模为素数的原因。
 
以上内容参考：https://blog.csdn.net/zhishengqianjun/article/details/79087525
 
还有一篇文章写的也不错，有具体代码验证：https://www.tianxiaobo.com/2018/01/18/String-hashCode-%E6%96%B9%E6%B3%95%E4%B8%BA%E4%BB%80%E4%B9%88%E9%80%89%E6%8B%A9%E6%95%B0%E5%AD%9731%E4%BD%9C%E4%B8%BA%E4%B9%98%E5%AD%90/

---

理论角度：

举例

给定一个整数的集合\(A=\{a_0,a_1,a_2,…,a_i\}\)，我们要对该集合里面的所有元素对数字 \(j\) 取余，那么 \(A\) 中所有元素取余后的值的集合\(B=\{0,1,2,…,j-1\}\)，取余实际上就是将集合 \(A\) 映射到集合 \(B\) 。

---

例1：取\(i=12\)，\(j=8\)，则有

---

例2：取\(i=12\)，\(j=8\)，则有

---

例3：取\(i=12\)，\(j=7\)，则有

以上例子表明：使用素数作为模数，可以提高余数空间的利用率
 
当然，如果原集合中的元素属于均匀分布或者接近均匀分布的话（元素间的值差均匀且较小），模数用素数和非素数的差距并不大（例1）。

 

数学证明

现在考虑 \(q\) 的情况：

---

以上内容参考：https://flat2010.github.io/2018/04/19/%E6%A8%A1%E8%BF%90%E7%AE%97%E4%B8%AD%E4%B8%BA%E4%BD%95%E8%A6%81%E7%94%A8%E7%B4%A0%E6%95%B0%E4%BD%9C%E4%B8%BA%E6%A8%A1/

总结：虽然说不能只考虑特定序列的一组数字，而是要考虑到更普遍的情况。但合数能应用的场景素数都能应用，素数能以不变应万变，稳赚不赔。。。
 

为什么要选择31

我们先看Jdk开发者之一兼《Effective Java》作者joshua.bloch在 https://bugs.java.com/bugdatabase/view_bug.do?bug_id=4045622 的回复（jdk1.1.1使用37处理短字符串，使用39处理长字符串）：

源码

public int hashCode() {
    int h = 0;
    int off = offset;
    char val[] = value;
    int len = count;

    if (len < 16) {
        for (int i = len ; i > 0; i--) {
            h = (h * 37) + val[off++];
        }
    } else {
        // only sample some characters
        int skip = len / 8;
        for (int i = len ; i > 0; i -= skip, off += skip) {
            h = (h * 39) + val[off];
        }
    }
    return h;
}

存在的问题

大意是原来的Java语言规范 JLS使用乘数39处理超过15个字符的字符串时会抛出异常，从而影响性能。

处理小字符串为什么用37已不可考。

 

解决方案

将乘数修正为31，是他经过大量研究的结果。而且对大字符串进行散列将更有效。

为什么候选乘数有31也不可考（即使是 Kernighan 和 Ritchie 也不记得它是从哪里来的）。

那么为什么我认为应该使用这个函数呢？简单地说，这是我能找到的最好的通用字符串哈希函数，而且计算成本很便宜。
 
所谓“通用”，我的意思是它没有针对任何特定类型的字符串（例如编译器符号）进行优化，但似乎可以抵抗我能够抛出的每个字符串集合之间的冲突。鉴于我们不知道人们将在Java哈希表中存储何种字符串，这一点至关重要。
 
还有这类哈希函数的性能似乎基本上不受哈希表大小是否为素数的影响。这一点很重要，因为Java的自动增长哈希表通常不包含素数个桶。（哈希表大小一般为2的幂，比如用int存储hash值，哈希表大小就为2^32）

 

几种候选乘数的比较

数据集：

1. 梅里亚姆·韦氏词典中所有词条的单词和短语（311141个字符串，平均长度10个字符）
2. 在/bin/*、/usr/bin/*、/usr/lib/*、/usr/ucb/*、/usr/openwin/bin/*中的所有字符串（66304个字符串，平均长度21个字符）
3. 由网络爬虫收集的URL列表（28372个字符串，平均长度49个字符）

哈希表平均查找次数（越小越好）：

结果分析：

看看这个表，很明显，除了Current Java Fn.、Weinberger's Fn(MatPak)、Weinberger's Fn(24)之外，所有函数都提供了极好的、几乎无法区分的性能。
 
我强烈猜测，这种性能本质上是“理论上的理想”，如果你用一个真正的随机数生成器来代替哈希函数，你就会得到这个结果。（现实数据的分布不太可能是完全随机分布）
 
我会排除WAIS Fn，因为它的规范包含随机数页，而且它的性能并不比任何远为简单的函数好。
 
剩下的六个功能中的任何一个看起来都是不错的选择，但我们必须选择一个。
 
我想我会排除Vo's Fn和Weinberger 函数，因为它们增加了复杂性，尽管很小。
 
在剩下的四个参数中（31,33,37,65599），我可能会选择31，因为在RISC（精简指令集计算机，比如单片机）机器上计算31是最便宜的（因为31是2的次幂减一）。
 
33计算起来也同样便宜，但它的性能稍微差一点，而33是复合的，这让我有点紧张（31 * i == (i << 5) - i,33 * i == (i << 5) + i，一个减法一个加法，加法可能溢出）

小结

通过以上分析，我们知道了31是开发者权衡了计算成本、兼容性（Java是个跨平台语言，考虑兼容小系统）、规范复杂性的综合选择，同时它又恰好是个素数（如序列{11,44,77}取31作为乘数比33更好）

那么用31作为乘数的哈希函数是好的吗？什么才是理想的哈希函数？它们有多大差距呢？

 

理想的哈希函数

int类型占 4 字节 32 位，有 \(2^{32}\) 种取值，但一个String常量可以包含任意数量的字符，考虑极端情况，由于鸽巢原理，碰撞/冲突必然存在。

著名的、反直觉的生日问题指出，对于365种可能的哈希值，在达到50%的碰撞概率时，至少存在23个唯一的哈希值，即使对于最理想的哈希函数也是如此。

如果有 \(2^{32}\) 种可能的哈希值，在达到50%的碰撞概率时，至少存在约77164个唯一的哈希值。

这个数字怎么来的？下面进行推导。
 

公式推导

假设散列函数非常好——它在可用范围内均匀分布散列值。

在这种情况下，为输入集合生成哈希值与生成随机数集合非常相似。那么，我们的问题可以转化为下面的问题：

给定 k 个随机值，每个值都小于 N，则它们中至少两个相等的概率是多少？

我们从反向思路着手，先计算它们都是唯一的概率。

给定一个由 N 个可能的散列值组成的序列。

假设已经选定一个值，还有 N-1 个值，它们都不等于选定的值，则随机两数相互不等的概率 \(p_1=\frac{N-1}{N}\)。

假设已经选定两个值，还有 N-2 个值，它们都不等于选定的值，则随机两数相互不等的概率 \(p_2=\frac{N-1}{N} \times \frac{N-2}{N}\)。（事件相互独立）

往后推到，得到所有数互相不等的概率 \(P_反=\frac{N-1}{N} \times \frac{N-2}{N} \times … \times \frac{N-(k-2)}{N} \times \frac{N-(k-1)}{N}\)。

该公式近似为：\(e^{\frac{-k(k-1)}{2N}}\)，原理是 \(e^x\) 泰勒展开式+等差公式，推导过程如下：

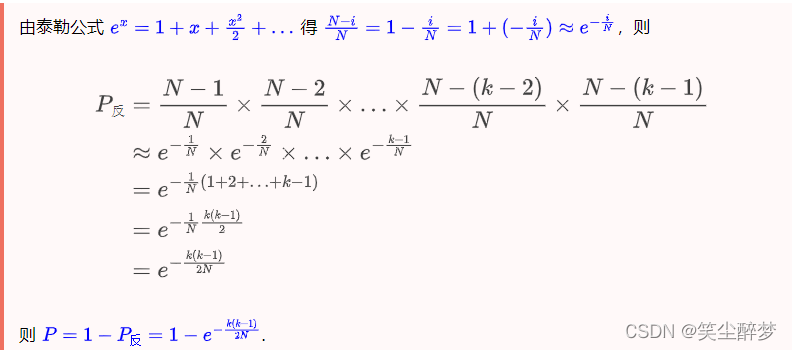
公式参考https://preshing.com/20110504/hash-collision-probabilities/

 

公式应用

令 \(N=2^{32}\)，则下图反映了使用 32 位哈希值时的冲突概率。

当哈希数为77163时，发生冲突的几率为50%，这个数字可以作为一个基准。

python代码：

from math import exp
def prob(x,N):
    return 1.0 -exp(-0.5 * x * (x-1) / N)

prob(77163,2**32) # 0.4999978150170551
prob(77164,2**32) # 0.500006797931095

换句话说，针对不同的数据集，碰撞最少的理想状态乘数分布在(0,getBorder(N,0.5))这个区间中，其中N是散列空间大小，0.5是碰撞率，getBorder()获取边界值，如上面的77163。

可以写个循环找到最少碰撞的乘数，代码如下：

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.io.IOException;

import java.util.*;

import java.nio.charset.StandardCharsets;

public class HashTest {

    //计算给定乘数x和数据长度N时的碰撞率
    public static double prob(int k, long N) {
        return 1 - Math.exp(-0.5 * k * (k - 1) / N);
    }

    //按碰撞率获取乘数的边界值
    public static int getBorder(long N, double rate) {
        int i = 0;
        int k = 0;
        while (i < N) {
            double result = prob(i, N);
            if (result > rate) {
                k = i - 1;
                break;
            }
            i++;
        }
        return k;
    }

    //获取理想状态的哈希值
    public static int getIdeaHashCode(String value, int k) {
        int hash = 0;
        for (int i = 0; i < value.length(); i++) {
            hash = k * hash + value.charAt(i);
        }
        return hash;
    }

    //统计碰撞集合，去重
    private static Map<Integer, Set> collisions(Collection values, int k, Boolean idea_on) {
        Map<Integer, Set> result = new HashMap<>();
        for (Object value : values) {
            Integer hc = (value.toString()).hashCode();//调用String.hashCode()
            if (idea_on) {	//如果要统计理想哈希值，调用该方法
                hc = HashTest.getIdeaHashCode((String) value, k);
            }
            Set bucket = result.get(hc);
            if (bucket == null)
                result.put(hc, bucket = new TreeSet<>());

            bucket.add(value);
        }
        return result;
    }

    //读入文本文件，寻找最少碰撞情况的乘数k，打印碰撞检测结果
    public static void test(String path, Boolean idea_on) throws IOException {
        System.err.println("Loading lines from stdin...");
        Set lines = new HashSet<>();
        try (BufferedReader r = new BufferedReader(new InputStreamReader(new FileInputStream(path), StandardCharsets.UTF_8))) {
            for (String line = r.readLine(); line != null; line = r.readLine())
                lines.add(line);
        }

        System.err.println("Computing collisions...");
        Map<Integer, Set> collisions;
        int max = 0;
        double rate = 0.5;
        for (double i = 0.5; i > 0; i -= 0.01) {	//调用循环找理想乘数
            collisions = collisions(lines, getBorder(lines.size(), i), idea_on);
            if (collisions.size() > max) {
                max = collisions.size();
                rate = i;
            }
        }
        int border = getBorder(lines.size(), rate);
        if (idea_on) {
            System.out.println("k = " + border);
        }
        collisions = collisions(lines, border, idea_on);

        int maxsize = 0;
        for (Map.Entry<Integer, Set> e : collisions.entrySet()) {
            Set bucket = e.getValue();
            if (bucket.size() > maxsize) {
                maxsize = bucket.size();
            }
        }

        System.out.println("Total unique lines: " + lines.size());
        System.out.println("Total unique hashcodes: " + collisions.size());
        System.out.println("Total collisions: " + (lines.size() - collisions.size()));
        System.out.println("Collision rate: " + String.format("%.8f", 1.0 * (lines.size() - collisions.size()) / lines.size()));
        if (maxsize != 0)
            System.out.println("Max collisions: " + maxsize);
    }

    public static void main(String[] args) throws IOException {
        test("D:\\code\\idea_projects\\Test\\src\\main\\resources\\words.txt", false);	//乘数31
        test("D:\\code\\idea_projects\\Test\\src\\main\\resources\\words.txt", true);	//理想状态下的乘数
        test("D:\\code\\idea_projects\\Test\\src\\main\\resources\\shakespeare.txt", false);	//乘数31
        test("D:\\code\\idea_projects\\Test\\src\\main\\resources\\shakespeare.txt", true);	//理想状态下的乘数
    }
}

数据集：

https://sigpwned.com/wp-content/uploads/2018/08/words.txt

https://sigpwned.com/wp-content/uploads/2018/08/shakespeare.txt

结果：

可以看出，String.hashCode()选择的31在这两个数据集的碰撞效果接近理想状态，表现良好。
 
对于不同分布的数据集，不同的乘数会产生不同的碰撞结果，众口难调，31可能不是最好的，但至少“不差”。
 
以上内容参考自：https://sigpwned.com/2018/08/10/string-hashcode-is-plenty-unique/

 

String.hashCode()的目的

https://www.reddit.com/r/programming/comments/967h8m/stringhashcode_is_not_even_a_little_unique/

哈希表/散列表一般有两种用途：加密 or 索引，这里将hashCode用作索引方便查找，没有必要花费额外的性能成本（比如调用安全散列函数）。

散列值可用于唯一地识别机密信息。这需要散列函数是抗碰撞(collision-resistant)的，意味着很难找到产生相同散列值的资料。
 
散列函数分类为密码散列函数和可证明的安全散列函数。第二类中的函数最安全，但对于大多数实际目的而言也太慢。透过生成非常大的散列值来部分地实现抗碰撞。例如，SHA-256是最广泛使用的密码散列函数之一，它生成256比特值的散列值。
 
https://zh.wikipedia.org/wiki/%E6%95%A3%E5%88%97%E5%87%BD%E6%95%B8

总结

• Java是一门跨平台的语言，31能提高小系统的运算效率（乘法转换为：移位+加法）
• 与合数相比，选择素数普适性更好
• 31不一定是最好的，但至少不差（与理想乘数相比）
• Java中String类型的对象大部分是常量，它的hashCode()只用作索引，没有必要花费更多计算成本提高安全性或保证无冲突，它是速度、碰撞次数、平台兼容性等多方面综合考虑的结果。