一、问题提出标题:可解释的视觉问题回答的概率神经符号模型
来源:ICML 2019https://proceedings.mlr.press/v97/vedantam19a.html
代码:https://github.com/kdexd/probnmn-clevr
neural-symbolic模型是神经和符号网络模型的结合。
神经网络参数的灵活可以挖掘到跟多的信息,但是缺乏解释性;
符号网络缺乏灵活的学习能力,但支持很强的泛化和系统性,且更加直观可解释。
本文从NMN出发,结合neural和program,深入探讨模型的推理能力。
对于VQA的image i 和question x, 生成一个程序program z, 利用program制定推理过程,使用神经网络进行具体运算。

例子:该例子中,基于问题,program首先从场景中过滤出cylinder和cube两个关键词,应用filter[cube]算子并关联[left],之后和filter[cylinder]一起预测答案。
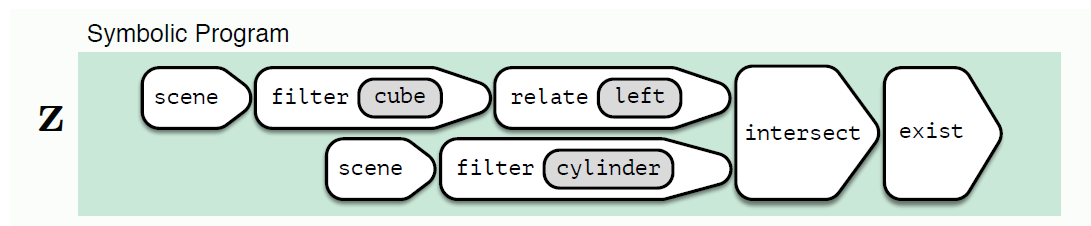
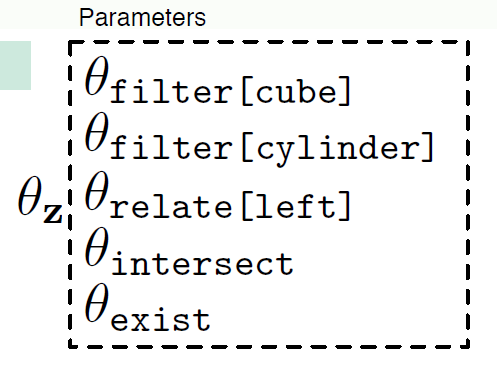
在构建program的过程中,将会动态产生一组参数θ,每一个参数代表一个模块。
本文的内容是在神经符号模型中引入了概率公式,通过这样的表达式,期望该模型满足可解释推理模型的一些自然需求。
二、主要思想问题形式化定义:
输入图像:\(i\in\ R^{U\times V}\)
输入问题:\(x=\left(x_1,...,x_t\right),\ \ x_t\in\ X\)
回答:\(a\in\ A\)
前缀序列化程序program:\(z=(z_1,...,z_t)\in\ Z\),其中给定符号\(z\in\ Z\),有一个对应的神经网络(后续可以动态的实例化神经网络)和参数\(\theta_z\)(给定z,这些都是确定的)。——该步定义类同于NMN神经模块网络中的模块
采用的数据集:
\[D=\{x^n,z^n\}\cup\{x^m,a^m,i^m\} \]\(\{x^m,a^m,i^m\}\):VQA数据集
\(\{x^n,z^n\}\):指引数据集,需要人工标注(为了探索模型的学习效果,期望N<<M,即使用很少的注释program得到很好的学习效果)
概率图模型:
分为两个步骤:Generative Model和Inference Network
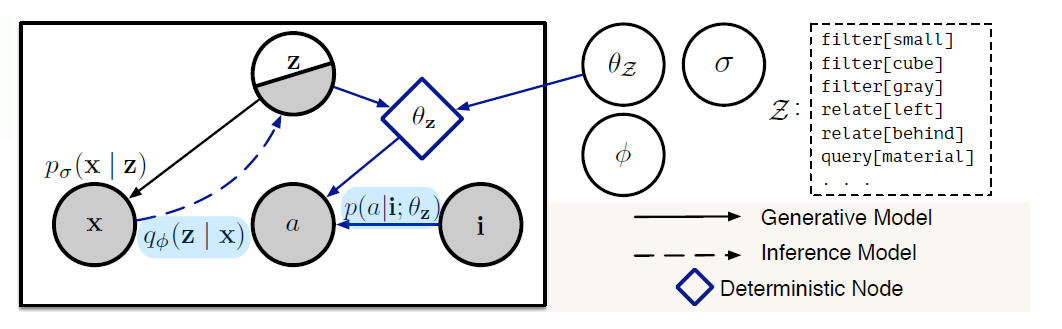
- Generative Model
给定图像i,建立\(p\left(x,z,a\middle|\ i\right)\)的模型,即关于问题、回答和program关系的模型。
模型分解为:
\[p\left(x,z,a\middle|\ i\right)=p\left(z\right)p\left(x\middle|\ z\right)p\left(a\middle|\ z,i\right) \]步骤:首先从program z的先验分布中采样一个program z,并通过该program z生成问题x;之后基于program z和输入的图片i,生成问题的答案。(此步骤中,z生成了问题x,但x不参与生成答案。)
其中,对program z里面的每一个项设置一种小的神经单元,动态地实例化神经网络的参数\(\theta_z\)(给定z,这些都是确定的)。——该步类同于NMN
从而:
\(p\left(a\middle|\ i,z\right)\)被化为\(p\left(a\middle|\ i,\theta_z\right)\),其中\(\theta_z=\{{\theta_{z_t}}\}_{t=1}^T\)。
从而:
\[p\left(x,z,a\middle|\ i\right)=p\left(z\right)p\left(x\middle|\ z\right)p\left(a\middle|\ i,z\right)=p\left(z\right)p\left(x\middle|\ z\right)p\left(a\middle|\ i,\theta_z\right) \]\(p\left(z\right)\)用最大似然法对关于program的封闭数据集进行预训练,并在之后保持固定,本文参数化为LSTM网络;
\(p_\sigma(x|z)\)同样参数化为LSTM网络;
\(\theta_z\)被参数化为CNN网络,将图片或者注意力作为输入,提取图中的感兴趣区域。
- Inference Network
推理过程,如图中虚线所示,首先通过问题生成program z,之后结合图片和生成的program,生成问题的答案。
文中不再使用NMN中parser+layout的结构,而是使用一个推理网络\(q_\emptyset(z|x)\)来映射问题到潜在的结构化程序program。
优点:融合了概率公式的NMN模型(Prob-NMN)可以带来更好的半监督学习和推理能力。
参数学习:
文中提出了一种三阶段优化算法:
- Question Coding
- Module Training
- Joint Training
- Question Coding
首先基于\(\{x^n,z^n\}\)以及\(x^m\),学习一个好的在潜空间z编码问题x的方法,即优化概率公式\(p_\sigma(x|z)\)、\(q_\emptyset(z|x)\) 。
目标:\(argmax\ \sum_{n}{log\ p\left(x^n\middle|\ z^n\right)}+\sum_{m}{log\ p\left(z^m\right)}\)
需要补充知识点:变分推断和摊销推理网络
参考知乎:
https://zhuanlan.zhihu.com/p/402237111
https://zhuanlan.zhihu.com/p/385341342
Step1:
先处理第二项\(\sum_{m}{log\ p\left(z^m\right)}\),利用摊销推理网络\(q_\emptyset\)优化证据下界( Evidence Lower Bound (ELBO)):
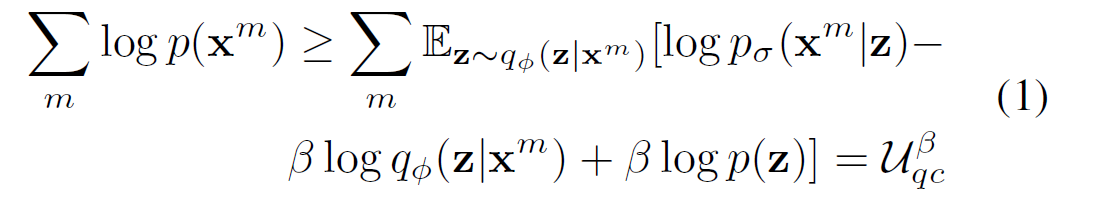
利用β < 1来衡量公式(1)中KL散度 \(D_{KL}(q(z|x)||p(z))\)的贡献。
该约束条件下,\(u_{qc}\)项没有捕获program的语义,即没有将其与特定的问题相关。所以还需要利用\(\{x^n,z^n\}\)学习问题和program之间的联系,并为问题x提供易读的解释。
Step2:
处理第一项\(\mathcal{L}=\sum_{n}{log\ p_\sigma\left(x^n\middle|\ z^n\right)+log\ p\left(z^n\right)}\),设序列z中第t个时间步的序列\(z_t\)分布为参数\(\pi_t\)的范畴。设\(\mathrm{\Pi}=\{\pi_t\}_{t=1}^T\)表示整个\(\pi_t\)上的联合随机变量,,按照相同的方法优化组合\(\mathcal{L}=\sum_{n}{log\ p_\sigma\left(x^n\middle|\ z^n\right)+log\ p\left(z^n\right)}\)的下界:
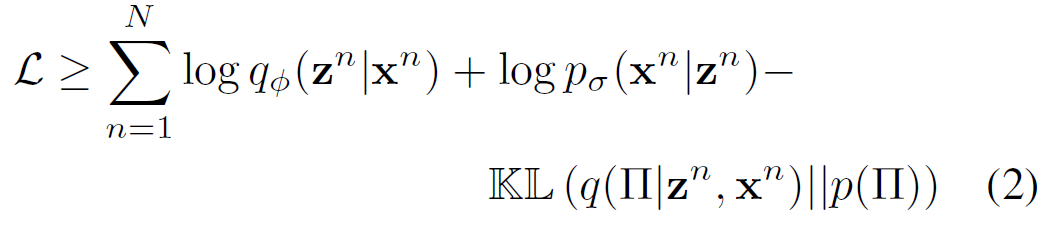
在实践中,由于后验\(q(\mathrm{\Pi}|z^n,x^n)\)会使得KL散度趋于∞,所以公式(2)中得到的下界没有意义。故改为对\(\mathcal{L}\)进行近似:
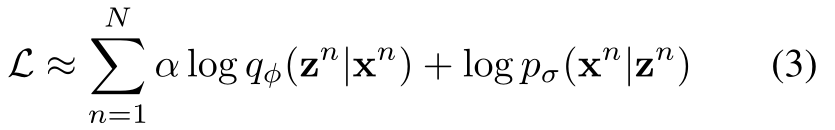
- Module Training
该阶段对模块进行优化,即优化参数\(\theta_Z\)。最大化:
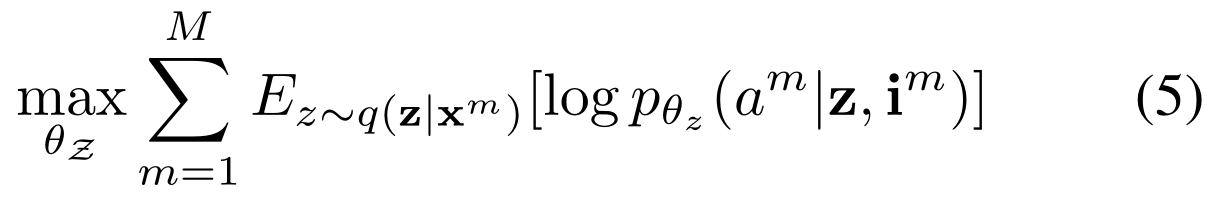
目标是找到模块参数的最佳初始化值。
例子:模块find [green] 的初始化参数\(\theta_{find\left[green\right]}\)将会约束该模块的执行达到预期的效果(即将图片中绿色部分加上注意力)。
- Joint Training
利用全部数据集\(D=x^n,z^n\cup x^m,a^m,i^m\),综合学习概率图模型的所有参数:\(\{\theta_Z,\sigma,\varphi\}\)。
目标:最大化\(\mathcal{L}+U_f\),其中\(U_f=\sum_{m=1}^{M}{log\ p\left(x^m,a^m\middle|\ i^m\right)}\),\(\mathcal{L}=\sum_{n=1}^{N}{log\ p\left(x^n,z^n\right)}\)。
按照步骤(1)类同的方法推导\(U_f\)的变分下界:
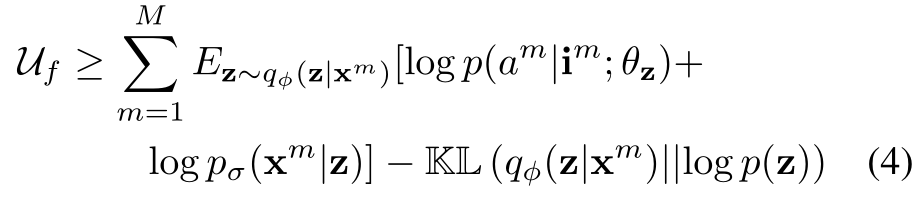
综合上述推导中的式(4)和式(3),将KL散度改写并加入期望中(参照知乎文章),并对相应项加入比例因子,得到最终的优化目标:
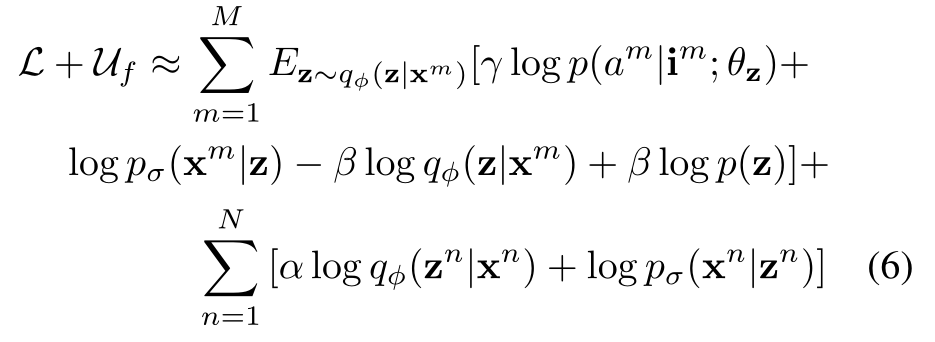
由于期望是关于\(\varphi\)不可微的,所以使用了一种REINFORCE估计器来获取\(\varphi\)的梯度估计。
最终的算法流程:

数据集:SHAPES CLEVR
结果:
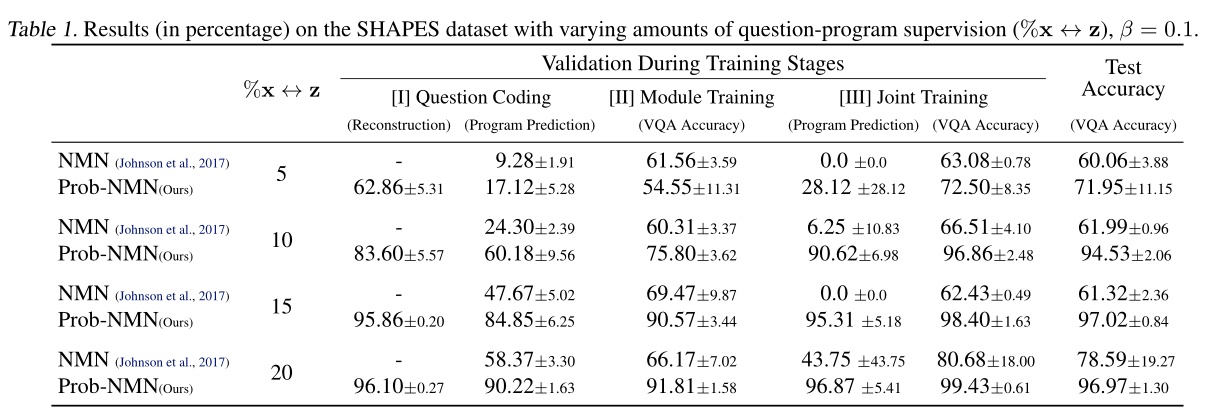
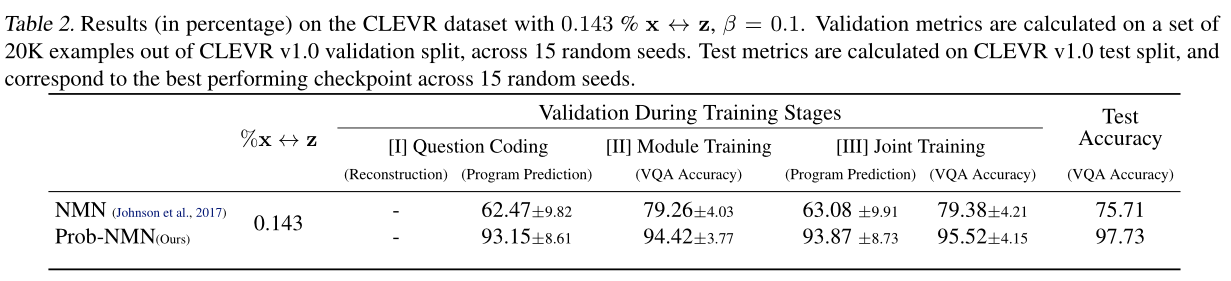
不同比例监督数据下的效果:
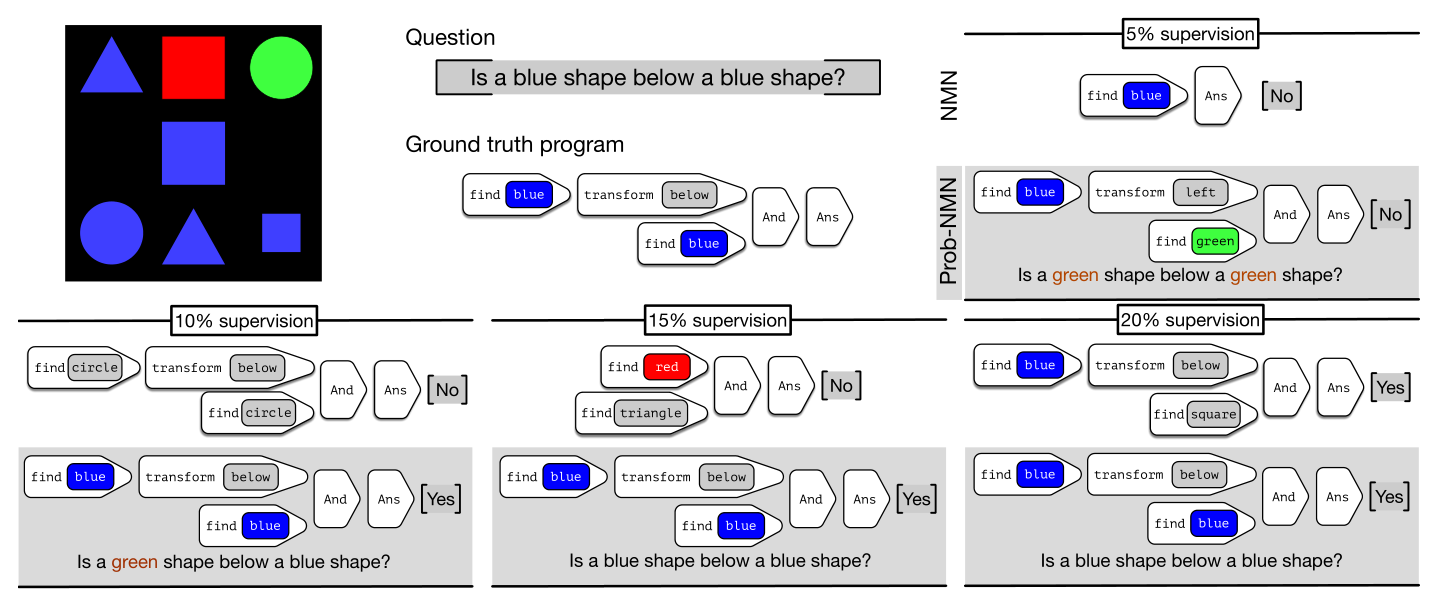
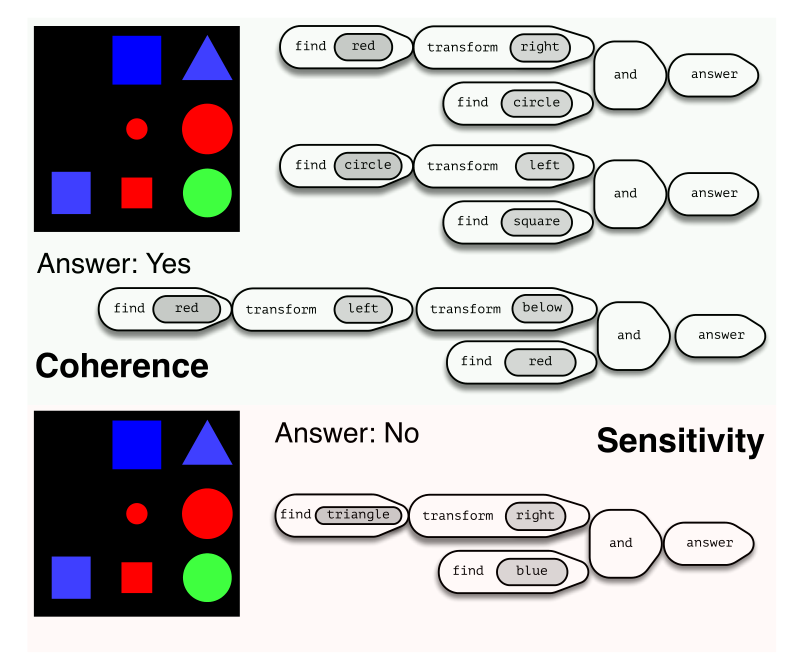
生成program的一致性和灵敏性:
文章工作:
- 模型为半监督学习,利用少量标记数据学习program的表示。
- 使用了概率模型,提升了模型的性能,使得生成的program 更加直接、易读、被理解。
- 用了反向推理的思路,通过给定答案(可能与事实不符),生成得到这个答案的program,提高了模型的解释性能。
- 三阶段训练策略:先预学习部分参数,便于联合学习获取更好的表现。
