- 八数码问题
- 遗传算法简介
- 设计思路
- 个体设计
- 适应度评价
- 其他部分
- 遗传算法流程
- 代码编写
- 实验结果
- 参数设置
- 求解问题
- 十五数码求解
- 对比 A* 算法
- 参考资料
八数码游戏(八数码问题)描述为:在 3×3 组成的九宫格棋盘上,摆有八个将牌,每一个将牌都刻有 1-8 八个数码中的某一个数码。棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。这种游戏求解的问题是:给定一种初始的将牌布局或结构(称初始状态)和一个目标的布局(称目标状态),问如何移动将牌,实现从初始状态到目标状态的转变。

遗传算法是通过模拟自然界中生物的遗传进化过程,对优化问题的最优解进行搜索的算法。算法维护一个代表问题潜在解的群体,对于群体的进化,算法引入了类似自然进化中选择、交配以及变异等算子。遗传算法搜索全局最优解的过程是一个不断选代的过程,每一次迭代相当于生物进化中的一次循环,直到满足算法的终止条件为止。
在遗传算法中,问题的每个有效解被称为一个“染色体(chromosome)”,相对于群体中的每个生物个体(individual)。染色体的具体形式是一个使用特定编码方式生成的编码串,编码串中的每一个编码单元称为“基因(gene)”。遗传算法通过比较适应值(fitness value)区分染色体的优劣,适应值越大的染色体越优秀,评估函数(evaluation function)用来计算并确定染色体对应的适应值。
为了在迭代中模拟生物进化的过程,遗传算法引入 3 个算子来实现。

遗传算法的实现主要包含了以下 6 个重要的部分,我们需要为这些重要的部分进行设计,使其可以解决八数码问题。
- 个体设计:问题的一个解的表示方式;
- 群体的初始化:用于算法进行迭代的初始种群;
- 适应度评价:评估各个染色体的适应值,进而区分优劣,常根据问题的优化目标来确定;
- 选择算子;
- 交叉算子;
- 变异算子。
首先是个体设计,由于八数码问题求解过程中的每一步都是数码“0”与其相邻数码交换,方向只有上下左右 4 个方向,因此一共是 4 种行为。我们可以为这 4 种行为进行编码,例如“1”表示数码 0 左移,“2”表示数码 0 “右移”,“3” 表示数码 0 上移,“4”表示数码 0 下移,这样一个可行解就可以表示为一个有多个编码组成的序列。
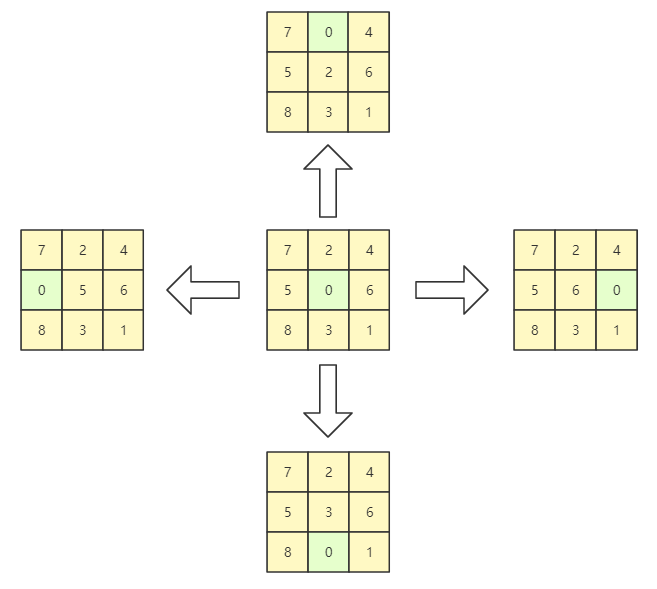
所以对于 GA 的个体设计可以使用线性表实现,线性表中的每个元素取自于(1,2,3,4)这个集合中,通过遍历这个线性表就可以获得一个数码 0 的移动序列,即可完成基因到表现型的翻译。
适应度评价方面决定了种群的优化方向,对于八数码问题而言适应度函数需要起到以下 2 个作用:
- 判断个体是否是可行解;
- 判断个体是否优于其他可行解。
在适应度的值越高表示个体越优秀的情况下,对于第一个作用,可以设置适应度为当前状态为:各个数码已经位于最终状态的个数。例如下图中的中间状态有 1、2、3、7、8 这五个数码已经位于最终状态,因此得到适应度为 5,而达到最优解个体的适应度应该为 9(或 8)。对于数码0是否计入适应度的问题,我认为计不计入都没有太大影响,因为对于一个可行解而言无论 0 是否计入适应度,其他 8 个数码都会在目标状态的位置下。
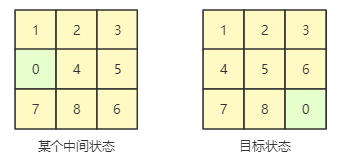
对于第二个作用,每个可行解中的数码在目标位置的个数是相同的,因此要挑选更好的个体则不能继续用这种度量方式。由于通过更少的步数使八个数码达到目标状态是更好的解,因此可以引入步数作为可行解优劣的度量方式。
得到的适应度计算公式如下,其中 state_matrix 表示某次移动后的状态矩阵,end_state 表示目标状态矩阵,k 为一个正数,count 为某个可行解的步数。步数较少的可行解,k/count 得到的适应度会更大,反之更小,所有的非可行解 k/count 的值直接置为 0 即可。

对于其他部分而言,由于 GA 在八数码问题中是基于一组初始的解法开始搜索,而每一个个体表达后的序列是否是可行解并不可知,因此只需要基于(1,2,3,4)这4个操作码生成随机序列作为初始种群即可。对于操作算子,八数码问题并不设计更为复杂的运算和操作,只要能改变个体的结构即可,因此可以使用原生的交叉、变异和选择算子。
遗传算法流程明确了以上重要部分的定义,就可以通过运行遗传算法求解八数码问题了,遗传算法的运行过程如下:
- 初始化规模为 N 的群体,其中染色体的每个基因的值随机生成;
- 采用评估函数对群体中所有染色体进行评价,计算每个染色体的适应值,保存适应值最大的染色体 Best;
- 对群体的染色体进行选择操作,产生规模同样为 N 的种群;
- 从种群中选择染色体进行交配,每两个父代染色体交换部分基因,产生两个新的子代染色体进入新种群,没有进行交配的染色体直接复制进入新种群;
- 对新种群中染色体的基因进行变异操作,发生变异的基因的数值发生改变,并取代原有染色体进入新群体,未发生变异的染色体直接进入新群体;
- 重新计算群体中各个染色体的适应值,若群体的最大适应值大于 Best 的适应值,则用其替代 Best;
- 如果 Generation 超过规定的最大进化代数或 Best 达到规定的误差要求,算法结束,否则返回 Step3。
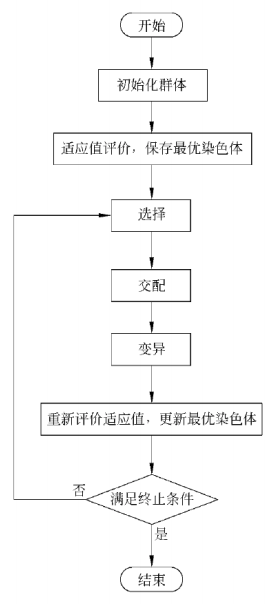
GA 算法基于 Python 的 DEAP 框架实现,关键在于编写适应度函数。注意如果遇到无效的操作码应该要跳过,而不是直接认为个体无效,这样可以使可行解出现得更容易。
# -*- coding: utf-8 -*-
"""
Created on Tue Mar 15 13:47:16 2022
@author: 12207
"""
import random
import numpy
from deap import creator, base, tools, algorithms
#起始状态矩阵
init_matrix = [[7, 2, 4],
[5, 0, 6],
[8, 3, 1]]
#目标状态矩阵
end_state = [[1, 2, 3],
[4, 5, 6],
[7, 8, 0]]
# 复制状态
def CopyState(state):
s = []
for i in state: s.append(i[:])
return s
# 获取空格的位置
def GetSpace(state):
for x in range(len(state)):
for y in range(len(state[x])):
if state[x][y] == 0:
return x, y
# 测试求解八数码问题
def test(individual, output = False):
# 保存 0 坐标和复制一份初始状态矩阵
x, y = GetSpace(init_matrix)
state_matrix = CopyState(init_matrix)
# 利用个体求解问题
action = []
for i in range(len(individual)):
flag = 0
#左移
if individual[i] == 0:
if y - 1 >= 0:
state_matrix[x][y] = state_matrix[x][y - 1]
state_matrix[x][y - 1] = 0
y = y - 1
action.append("左移")
flag = 1
else:
continue
#右移
elif individual[i] == 1:
if y + 1 < len(state_matrix[0]):
state_matrix[x][y] = state_matrix[x][y + 1]
state_matrix[x][y + 1] = 0
y = y + 1
action.append("右移")
flag = 1
else:
continue
#上移
elif individual[i] == 2:
if x - 1 >= 0:
state_matrix[x][y] = state_matrix[x - 1][y]
state_matrix[x - 1][y] = 0
x = x - 1
action.append("上移")
flag = 1
else:
continue
#下移
else:
if x + 1 < len(state_matrix[0]):
state_matrix[x][y] = state_matrix[x + 1][y]
state_matrix[x + 1][y] = 0
x = x + 1
action.append("下移")
flag = 1
else:
continue
#记录行动
if output == True:
if flag == 1:
print("第" + str(len(action)) + "次行动:" + action[-1])
for l in range(len(state_matrix)):
print(state_matrix[l])
print()
#检查是否满足可行解
fitness = 0
for j in range(len(state_matrix)):
for k in range(len(state_matrix[0])):
if state_matrix[j][k] == end_state[j][k]:
fitness += 1
if fitness == len(state_matrix) * len(state_matrix[0]):
fitness += 100 / len(action)
break
#输出结果
if output == True:
print("共需要:" + str(len(action)) + " 步")
print(action)
#返回适应度
return fitness
# 适应度函数
def evaluate(individual):
return test(individual),
# 定义问题和个体
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)
# 注册个体和种群
toolbox = base.Toolbox()
toolbox.register("attr_bool", random.randint, 0, 3)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n = 100)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# 注册操作算子
toolbox.register("evaluate", evaluate)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
# 定义迭代数和精英数
pop = toolbox.population(n = 800)
hof = tools.HallOfFame(1)
# 设置显示的迭代信息
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", numpy.mean)
stats.register("std", numpy.std)
stats.register("min", numpy.min)
stats.register("max", numpy.max)
# 运行GA
pop, log = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.5, ngen = 150,
stats=stats, halloffame=hof, verbose=True)
# 取到一次迭代的最优个体
best_ind = tools.selBest(pop, 1)[0]
print("Best individual is %s" % (best_ind.fitness.values))
# 用该个体求解八数码问题
test(best_ind, True)
遗传算法涉及到多个超参数,对于不同参数的设置都会影响 GA 是否能求得可行解,以及可行解是否能逼近最优解。 GA 涉及到的参数和本次实验使用的设置如下:
这些参数的设置是通过多次实验得到的,实验证明这样设置参数更容易获得可行解,且可行解更容易是最优解。
- 对于个体长度而言太长或太短都不适合,太短则操作码序列不易组合成一个可行解,太长则操作码序列中的大量基因都会成为无效基因,影响交叉变异操作;
- 对于种群而言,可以稍微设置的大一些,因为种群大小越大,个体类型越丰富,种群中越容易出现可行解,但是种群大小如果太大则会影响算法运行的时间;
- 对于迭代次数而言如果设置得太小,则很有可能在找到一个可行解之前就停止迭代导致无解,如果设置过大则会在求得可行解并完成优化后继续迭代,导致运行时间过长;
- 其他参数我认为需要通过实验来观察他们对算法的影响,以调制一个相对较好的参数。
经过多次实验后,GA 可以对如下八数码问题求得20步(最优解)、22 步、24 步、26 步和无解等多种可行解,由于参数设置合理出现前 3 种解的概率更高。
其中 20 步解的 GA 迭代过程和算法模拟的过程如下:
gen nevals avg std min max
0 800 0.916154 1.02216 0 10.9231
1 675 1.15125 1.01038 0 6
2 697 1.30375 1.059 0 6
3 678 1.50375 1.13247 0 6
4 678 1.66625 1.16184 0 6
5 716 1.71875 1.12457 0 6
6 676 1.90875 1.15344 0 6
7 693 2.015 1.13238 0 6
8 693 2.09875 1.21099 0 6
9 658 2.23625 1.20952 0 6
10 664 2.335 1.31919 0 6
11 677 2.34 1.29688 0 6
12 659 2.32375 1.27532 0 6
13 700 2.26125 1.27201 0 6
14 677 2.29716 1.35114 0 10.7241
15 661 2.37966 1.35083 0 10.7241
16 681 2.34841 1.38519 0 10.7241
17 683 2.38125 1.38145 0 6
18 668 2.37 1.33439 0 6
19 673 2.48424 1.31709 0 10.3889
20 661 2.47597 1.41841 0 10.3889
21 677 2.42424 1.3745 0 10.3889
22 699 2.38924 1.3812 0 10.3889
23 681 2.4875 1.3729 0 6
24 680 2.51125 1.4124 0 6
25 673 2.56583 1.39238 0 10.6667
26 680 2.51606 1.34411 0 10.8519
27 691 2.53238 1.5046 0 10.8519
28 677 2.61463 1.42061 0 10.8519
29 681 2.66625 1.38559 0 6
30 686 2.735 1.4568 0 7
31 689 2.7725 1.45026 0 6
32 678 2.74625 1.50062 0 6
33 664 2.85625 1.54534 0 7
34 679 2.97125 1.5868 0 7
35 690 3.0375 1.54874 0 7
36 683 3.06966 1.59835 0 10.7241
37 682 3.17181 1.627 0 10.7241
38 676 3.23285 1.68392 0 10.8519
39 692 3.28214 1.74118 0 10.7241
40 664 3.38493 1.78097 0 10.7241
41 694 3.4483 1.93238 0 11
42 678 3.41232 1.92737 0 11
43 658 3.49972 1.94429 0 10.9231
44 661 3.51843 1.80648 0 10.7857
45 690 3.47305 1.85472 0 11.0833
46 713 3.47086 1.78452 0 10.7241
47 672 3.59817 1.92064 0 10.7857
48 691 3.73408 1.85666 0 11.1739
49 674 3.67482 1.89536 0 11.1739
50 673 3.80356 1.96122 0 10.7857
51 700 3.80797 2.07383 0 11.1739
52 674 3.90646 2.09275 0 11.1739
53 674 4.06944 2.07941 0 10.9231
54 686 4.12545 2.34007 0 10.9231
55 688 4.15162 2.42984 0 10.9231
56 681 4.35468 2.5445 0 10.9231
57 691 4.54398 2.67036 0 11.0833
58 670 4.71895 2.89572 0 11.0833
59 692 4.86082 3.0268 0 11.1739
60 687 4.86067 3.02529 0 11.1739
61 678 5.20179 3.1747 0 11.5
62 677 5.38734 3.28693 0 11.1739
63 693 5.43769 3.42671 0 11.0833
64 683 5.85496 3.61262 0 11.0833
65 700 6.04815 3.62355 0 11.1739
66 681 6.35203 3.55131 0 11.2727
67 695 6.35581 3.63976 0 11.1739
68 669 6.68934 3.66771 0 11.2727
69 676 6.85206 3.63175 0 11.1739
70 677 7.02204 3.73915 0 11.2727
71 672 7.05675 3.73708 0 11.2727
72 671 7.40174 3.6965 0 11.2727
73 691 7.2454 3.73567 0 11.381
74 703 7.37047 3.81093 0 11.381
75 678 7.72293 3.73864 0 11.6316
76 665 7.74398 3.8379 0 11.6316
77 697 7.65846 3.89477 0 11.7778
78 670 8.10184 3.71352 0 11.9412
79 679 7.87819 3.93109 0 12.3333
80 693 7.91455 3.88636 0 11.9412
81 664 8.08672 3.92568 0 12.3333
82 681 8.00442 3.9587 0 12.3333
83 669 8.17642 3.97659 0 12.3333
84 684 8.33876 3.94409 0 12.3333
85 693 8.39025 3.97392 0 12.5714
86 655 8.61277 3.99659 0 12.5714
87 653 8.58687 4.0956 0 12.5714
88 698 8.75961 3.99942 0 13.1667
89 674 8.64706 4.07755 0 13.5455
90 682 8.70197 4.14737 0 13.1667
91 678 8.5173 4.24908 0 13.1667
92 683 8.68691 4.26711 0 13.5455
93 685 8.5834 4.31516 0 13.5455
94 690 8.73941 4.31766 0 13.5455
95 661 8.78165 4.36963 0 13.5455
96 677 8.85828 4.43163 0 13.5455
97 655 9.17691 4.3403 0 14
98 683 9.21458 4.35707 0 14
99 677 9.18711 4.43829 0 14
100 687 9.36876 4.41648 0 14
101 690 9.03331 4.65563 0 14
102 671 9.29202 4.56312 0 14
103 667 9.18334 4.6617 0 14
104 682 9.52724 4.56026 0 14
105 675 9.22975 4.70255 0 14
106 696 9.39653 4.56519 0 14
107 664 9.78237 4.5261 0 14
108 691 9.44421 4.72645 0 14
109 691 9.51576 4.70129 0 14
110 675 9.60297 4.72857 0 14
111 689 9.58822 4.71084 0 14
112 672 9.8205 4.80112 0 14
113 692 9.78278 4.8189 0 14
114 688 10.0249 4.70473 0 14
115 671 9.80663 4.81124 0 14
116 678 9.87802 4.9157 0 14
117 678 9.44586 4.97813 0 14
118 703 9.76003 4.88581 0 14
119 689 9.91857 4.86126 0 14
120 698 9.67992 4.91348 0 14
121 690 9.68896 4.85831 0 14
122 680 9.4835 4.98717 0 14
123 652 9.75117 4.92572 0 14
124 660 9.90767 4.80053 0 14
125 678 9.35005 4.9746 0 14
126 680 9.34913 4.93231 0 14
127 689 9.66326 4.91036 0 14
128 676 9.68926 4.91103 0 14
129 701 9.58734 4.9814 0 14
130 671 9.86524 4.89669 0 14
131 684 9.73642 4.84656 0 14
132 678 9.66712 4.94382 0 14
133 683 9.76349 4.77846 0 14
134 639 10.1327 4.68325 0 14
135 646 10.1052 4.81449 0 14
136 672 9.68233 4.97427 0 14
137 693 9.89786 4.81054 0 14
138 685 9.75015 4.91675 0 14
139 689 9.66459 4.96552 0 14
140 682 9.68376 4.91367 0 14
141 676 9.93599 4.75792 0 14
142 673 9.70179 4.85661 0 14
143 693 9.64158 4.83251 0 14
144 675 9.76849 4.76896 0 14
145 686 9.67357 4.8312 0 14
146 663 9.51975 4.81826 0 14
147 677 9.81509 4.75262 0 14
148 673 9.89897 4.75189 0 14
149 679 10.2556 4.62767 0 14
150 682 9.95908 4.76826 0 14
Best individual is 14.0
求得的最优个体转换为操作码序列,然后进行求解的过程如下:
['下移', '右移', '上移', '左移', '左移', '上移', '右移', '右移', '下移', '左移', '下移', '左移', '上移', '右移', '上移', '左移', '下移', '右移', '右移', '下移']
第1次行动:下移
[7, 2, 4]
[5, 3, 6]
[8, 0, 1]
第2次行动:右移
[7, 2, 4]
[5, 3, 6]
[8, 1, 0]
第3次行动:上移
[7, 2, 4]
[5, 3, 0]
[8, 1, 6]
第4次行动:左移
[7, 2, 4]
[5, 0, 3]
[8, 1, 6]
第5次行动:左移
[7, 2, 4]
[0, 5, 3]
[8, 1, 6]
第6次行动:上移
[0, 2, 4]
[7, 5, 3]
[8, 1, 6]
第7次行动:右移
[2, 0, 4]
[7, 5, 3]
[8, 1, 6]
第8次行动:右移
[2, 4, 0]
[7, 5, 3]
[8, 1, 6]
第9次行动:下移
[2, 4, 3]
[7, 5, 0]
[8, 1, 6]
第10次行动:左移
[2, 4, 3]
[7, 0, 5]
[8, 1, 6]
第11次行动:下移
[2, 4, 3]
[7, 1, 5]
[8, 0, 6]
第12次行动:左移
[2, 4, 3]
[7, 1, 5]
[0, 8, 6]
第13次行动:上移
[2, 4, 3]
[0, 1, 5]
[7, 8, 6]
第14次行动:右移
[2, 4, 3]
[1, 0, 5]
[7, 8, 6]
第15次行动:上移
[2, 0, 3]
[1, 4, 5]
[7, 8, 6]
第16次行动:左移
[0, 2, 3]
[1, 4, 5]
[7, 8, 6]
第17次行动:下移
[1, 2, 3]
[0, 4, 5]
[7, 8, 6]
第18次行动:右移
[1, 2, 3]
[4, 0, 5]
[7, 8, 6]
第19次行动:右移
[1, 2, 3]
[4, 5, 0]
[7, 8, 6]
第20次行动:下移
[1, 2, 3]
[4, 5, 6]
[7, 8, 0]
共需要:20 步
同时我也顺便做了 15 数码问题的实验,设置的参数如下所示:
经过多次实验后,GA 可以对如下十五数码问题求得 14 步(最优解)、16 步、18 步、20 步和无解等多种可行解,由于参数设置合理出现前3种解的概率更高。
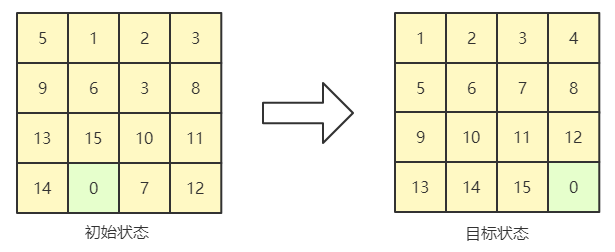
其中 14 步解的 GA 迭代过程如下:
gen nevals avg std min max
0 500 2.804 1.89778 0 10
1 455 3.61 2.00347 0 10
2 406 4.226 2.01368 0 13
3 420 4.55 2.16876 0 13
4 432 4.74 2.27253 0 13
5 430 5.136 2.17566 0 14
6 420 5.396 2.24481 0 14
7 418 5.96 2.43524 0 14
8 411 6.176 2.59943 1 14
9 418 6.532 2.63685 0 13
10 423 6.82273 2.85749 0 17.8519
11 434 7.0797 2.8077 0 17.8519
12 431 7.13312 2.9915 0 17.9231
13 433 7.59525 3.03271 0 17.9231
14 430 7.8597 2.91932 1 18
15 416 8.16896 3.15923 1 18
16 413 8.7058 3.12672 0 18.381
17 421 8.9332 3.02184 1 18.1739
18 428 9.03772 3.27725 1 18.5
19 423 9.43106 3.19378 1 18.6316
20 425 9.82126 3.17837 1 18.6316
21 415 10.5461 3.16456 2 18.5
22 428 10.7476 3.35155 2 18.5
23 438 10.9505 3.47476 1 18.5
24 437 11.074 3.7309 2 18.7778
25 430 11.6376 3.79662 2 18.7778
26 435 11.6367 4.14556 1 18.9412
27 413 11.9898 4.38395 2 18.9412
28 420 12.7597 4.50714 3 18.9412
29 427 13.1177 4.44418 2 19.125
30 435 12.9664 4.72083 2 19.3333
31 442 13.6065 4.39273 2 19.5714
32 413 13.6956 4.51632 2 19.8462
33 418 14.0886 4.50137 3 19.8462
34 428 14.2752 4.6699 2 20.1667
35 409 14.603 4.70739 2 20.1667
36 429 15.054 4.54146 2 20.1667
37 420 15.26 4.69613 2 20.5455
38 424 15.3826 4.6169 3 20.5455
39 425 15.5825 4.86051 2 20.5455
40 415 16.0692 4.80273 3 21
41 432 16.052 4.97239 3 21.5556
42 416 16.252 5.05336 0 21.5556
43 433 16.829 4.79003 4 21.5556
44 428 17.1049 4.70856 4 22.25
45 415 16.8963 5.1402 3 22.25
46 420 17.462 4.86248 4 22.25
47 427 17.1116 5.26254 3 23.1429
48 411 17.6386 5.0697 4 23.1429
49 436 17.6618 5.22843 3 23.1429
50 432 17.94 5.23996 3 23.1429
51 447 18.227 5.34326 2 23.1429
52 446 18.5562 5.25413 4 23.1429
53 419 18.7661 5.19452 4 23.1429
54 453 18.4708 5.42239 4 23.1429
55 412 19.1343 5.11742 5 23.1429
56 429 18.724 5.53154 2 23.1429
57 415 18.9125 5.42473 4 23.1429
58 420 18.7524 5.51772 2 23.1429
59 408 18.4968 5.81073 2 23.1429
60 426 18.8919 5.6346 2 23.1429
61 425 18.6763 5.72745 1 23.1429
62 440 19.0743 5.53242 3 23.1429
63 420 19.4044 5.38224 2 23.1429
64 402 19.0829 5.7189 3 23.1429
65 420 19.1684 5.61303 3 23.1429
66 411 19.6009 5.49468 3 23.1429
67 432 18.8824 5.83395 3 23.1429
68 438 18.9075 5.75353 4 23.1429
69 410 18.7874 5.93363 3 23.1429
70 427 18.9897 5.76009 2 23.1429
71 431 19.4343 5.55504 4 23.1429
72 400 18.8594 6.04564 3 23.1429
73 428 19.015 5.8188 2 23.1429
74 423 19.29 5.80855 3 23.1429
75 442 18.262 6.25965 4 23.1429
76 418 19.2296 5.70333 2 23.1429
77 424 19.1242 5.8113 2 23.1429
78 427 18.8145 6.03968 4 23.1429
79 419 19.3995 5.57845 2 23.1429
80 430 19.2223 5.70262 4 23.1429
81 419 18.751 5.97296 4 23.1429
82 434 19.0121 5.84478 3 23.1429
83 423 18.454 6.19559 2 23.1429
84 417 18.7456 6.03199 3 23.1429
85 431 18.8156 5.93744 2 23.1429
86 435 19.0928 5.76365 3 23.1429
87 436 18.6646 6.15669 3 23.1429
88 405 18.7848 6.0336 1 23.1429
89 424 18.9909 5.88768 2 23.1429
90 437 18.3604 6.302 1 23.1429
91 437 18.605 6.22241 3 23.1429
92 436 18.1165 6.43491 2 23.1429
93 429 18.8608 5.85384 4 23.1429
94 440 18.6587 6.11432 3 23.1429
95 442 18.819 5.90563 3 23.1429
96 424 18.7152 6.09943 2 23.1429
97 415 18.804 6.03523 3 23.1429
98 418 18.543 6.23341 2 23.1429
99 446 18.4038 6.29188 3 23.1429
100 420 19.0295 5.89556 4 23.1429
Best individual is 23.142857142857142
求得的最优个体转换为操作码序列,然后进行求解的过程如下:
['上移', '右移', '下移', '左移', '左移', '上移', '上移', '上移', '右移', '右移', '下移', '下移', '右移', '下移']
第1次行动:上移
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 0, 10, 11]
[14, 15, 7, 12]
第2次行动:右移
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 0, 11]
[14, 15, 7, 12]
第3次行动:下移
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[14, 15, 0, 12]
第4次行动:左移
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[14, 0, 15, 12]
第5次行动:左移
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[0, 14, 15, 12]
第6次行动:上移
[5, 1, 2, 4]
[9, 6, 3, 8]
[0, 10, 7, 11]
[13, 14, 15, 12]
第7次行动:上移
[5, 1, 2, 4]
[0, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
第8次行动:上移
[0, 1, 2, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
第9次行动:右移
[1, 0, 2, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
第10次行动:右移
[1, 2, 0, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
第11次行动:下移
[1, 2, 3, 4]
[5, 6, 0, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
第12次行动:下移
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 0, 11]
[13, 14, 15, 12]
第13次行动:右移
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 0]
[13, 14, 15, 12]
第14次行动:下移
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 12]
[13, 14, 15, 0]
共需要:14 步
由于 A* 算法不属于智能计算算法,无论是算法过程还是启发函数计算都是确定的,因此使用 A* 算法得到的解也是确定的。在八数码问题中,从初始状态到当前状态的代价就用移动的步数表示,从当前状态到目标状态的估计代价就用所有数码与它们的最终位置的曼哈顿距离表示。由于问题规模和八数码问题本身的最优求解策略而言,这种设置下求得的解只有一种且为最优解。
个人认为对于八数码这类规模小、问题复杂度低、具有明确的求解策略的问题,显然 A* 算法更为合适。因为 A* 算法的启发策略很简单,非常契合八数码问题本身,即只需要在有限的搜索空间和有限的搜索能力上,按照明确的求解策略来执行即可得到最优解。
而 GA 则需要为八数码问题设计个体的形式,设计适应度的评估函数,指定相关的操作算子并进行迭代后才能求得可行解,在合适的参数和足够多次的实验下可以求得最优解。这是因为 GA 算法是一个通用的算法框架,只需要对个体和适应度的评估方式进行合理地设计,即可求解最优化问题,其他能求解最优化问题的智能计算算法也可以做到。
同时 GA 进行的是一种对于全局的搜索,它的搜索空间和搜索能力远高于 A* 算法,但是搜索的方式相对而言就显得更加随机,更加盲目。因此对于八数码问题而言反倒不是最优的解法,但是 GA 也可以提供更多的可行解拓展我们对问题的认知,GA 更适合用于对一些 NP 难问题或者一些复杂的最优化问题进行求解。
《计算智能》,张军 詹志辉 等编著,清华大学出版社
DEAP documentation
