机器学习—聚类5-1（K-Means算法+瑞士卷）

使用K-Means对超市客户分组

主要步骤流程：

• 1. 导入包
• 2. 导入数据集
• 3. 使用肘部法则选择最优的K值
• 4. 使用K=5做聚类
• 5. 可视化聚类效果
• 6. 采取措施
• 7. 瑞士卷生产及其聚类

   数据集链接：https://www.heywhale.com/mw/dataset/6230697d5f17950018ee88b5/file   1. 导入包 In [1]:

# 导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

 

2. 导入数据集 In [2]:

# 导入数据集
dataset = pd.read_csv('Mall_Customers.csv')
dataset

Out[2]:  CustomerIDGenreAgeAnnual Income (k$)Spending Score (1-100) 0 1 Male 19 15 39 1 2 Male 21 15 81 2 3 Female 20 16 6 3 4 Female 23 16 77 4 5 Female 31 17 40 ... ... ... ... ... ... 195 196 Female 35 120 79 196 197 Female 45 126 28 197 198 Male 32 126 74 198 199 Male 32 137 18 199 200 Male 30 137 83

200 rows × 5 columns

为了可视化聚类效果，仅选取Annual Income (k$)和Spending Score (1-100)这2个字段

In [3]:

X = dataset.iloc[:, [3, 4]].values
X[:3, :]

Out[3]:

array([[15, 39],
       [15, 81],
       [16,  6]], dtype=int64)

  3. 使用肘部法则选择最优的K值 In [4]:

# 使用肘部法则选择最优的K值
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', n_init=10, max_iter=300, random_state = 0)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)

In [5]:

# 画出 聚类个数 vs WCSS 图
plt.figure()
plt.plot(range(1, 11), wcss, 'ro-')
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()

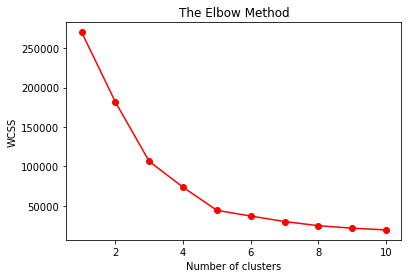
从K=5开始，WCSS下降的不再明显，说明K=5是最优选择

  4. 使用K=5做聚类 In [6]:

# 使用选择出的K，使用K-Means做聚类
kmeans = KMeans(n_clusters = 5, init = 'k-means++', n_init=10, max_iter=300, random_state = 0)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

In [7]:

y_kmeans

Out[7]:

array([3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1,
       3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 0,
       3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 4, 2, 0, 2, 4, 2, 4, 2,
       0, 2, 4, 2, 4, 2, 4, 2, 4, 2, 0, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
       4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
       4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
       4, 2])

5. 可视化聚类效果 In [8]:

# 可视化聚类效果
plt.figure()
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 100, c = 'red', label = 'Cluster 1')
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Cluster 2')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Cluster 3')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4')
plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 300, c = 'yellow', label = 'Centroids')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()

  6. 采取措施

1. Cluster 1 工资收入中等，消费中等；
2. Cluster 2 工资收入低，消费高，查看这个分组主要购买哪些商品；
3. Cluster 3 工资收入高，消费高；
4. Cluster 4 工资收入低，消费低；
5. Cluster 5 工资收入高，消费低，给这个分组的客户办理优惠券或打折购物卡，吸引他们消费；

 

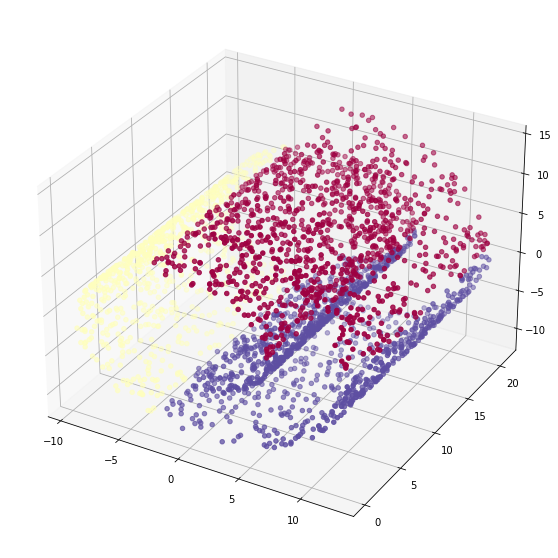
7. 瑞士卷生产及其聚类 In [10]:

from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn import manifold, datasets
import matplotlib.pyplot as plt
​

#生成带噪声的瑞士卷数据集
X,color = datasets.make_swiss_roll(n_samples=3000)
​
#使用100个K-means簇对数据进行近似
clusters_swiss_roll = KMeans(n_clusters=3,random_state=1).fit_predict(X)
​
fig2 = plt.figure(figsize=(10,10))

ax = fig2.add_subplot(111,projection='3d')
ax.scatter(X[:,0],X[:,1],X[:,2],c = clusters_swiss_roll,cmap = 'Spectral')

plt.show()

如上图，根据距离将其聚成了3类，