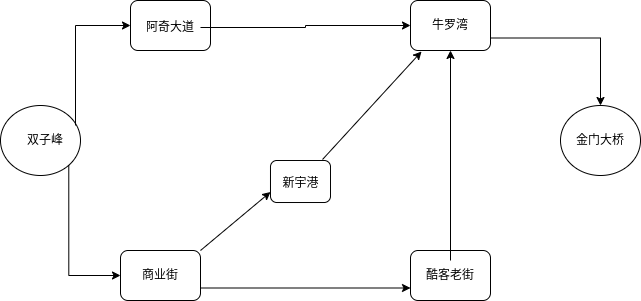
广度搜索和深度搜索

广度搜索和深度搜索 最短路径问题

我现在要从“双子峰” 前往 “金门大桥” ，求最短的路径

根据图建立树 根据图建立二叉树模型

package DataStructure.FS;

public class PlaceTree {
    //存储当前地址
    String place;
    //左孩子节点
    PlaceTree leftPlace;
    //右孩子节点
    PlaceTree rightPlace;

    //无参构造方法
    public PlaceTree() {
    }

    //带单独参构造方法
    public PlaceTree(String p){
        place = p;
    }

    //带全参的构造方法
    public PlaceTree(PlaceTree left,PlaceTree right,String p){
        //放置左孩子
        leftPlace = left;
        //放置右孩子
        rightPlace = right;
        //放置位置
        place = p;
    }

}

实现二叉树

 public static void main(String[] args) {
        PlaceTree szf = new PlaceTree("双子峰");
        PlaceTree aqdd = new PlaceTree("阿奇大道");
        PlaceTree syj = new PlaceTree("商业街");
        PlaceTree llw = new PlaceTree("牛罗湾");
        PlaceTree xyg = new PlaceTree("新宇港");
        PlaceTree kklj = new PlaceTree("酷客老街");
        PlaceTree jmdq = new PlaceTree("金门大桥");
        //创建节点
        szf.leftPlace = aqdd;
        szf.rightPlace = syj;
        aqdd.rightPlace = llw;
        syj.leftPlace = xyg;
        syj.rightPlace = kklj;
        xyg.rightPlace = llw;
        kklj.rightPlace = llw;
        llw.rightPlace = jmdq;
        //设置关系

        System.out.println("广度优先遍历结果:");
        new PlaceBFS().BroadFirstSearch(szf);

        System.out.println("深度优先遍历结果:");
        new PlaceBFS().DepthFirstSearch(szf);
    }

实现 BFS 广度搜索

 public void BroadFirstSearch(PlaceTree nodeHead){
        //如果节点为空，返回
        if(nodeHead == null)
            return;
        //以队列的方式 (FIFO) 实现广度搜索
        Queue<PlaceTree> myQueue = new LinkedList<>();
        myQueue.add(nodeHead);
        //将节点压入队列
        while(! myQueue.isEmpty()){
            PlaceTree node = myQueue.poll();
                System.out.print(node.place + " ");
                if (null != node.leftPlace) {
                    myQueue.add(node.leftPlace);
                    //有左孩子就压左孩子
                }
                if (null != node.rightPlace) {
                    myQueue.add(node.rightPlace);
                    //有右孩子就压有孩子
                }
                //呈现右孩子和右孩子都压入队列中的情况，这样说好恐怖。
        }
    }

实现 DFS 深度搜索

public void DepthFirstSearch(PlaceTree nodeHead){
        if(nodeHead == null){
            return;
        }
        //以堆栈 (LIFO) 实现深度搜索
        Stack<PlaceTree> myStack = new Stack<>();
        myStack.add(nodeHead);
        while(! myStack.isEmpty()){
            PlaceTree node = myStack.pop();
            System.out.print(node.place+" ");
            if(node.rightPlace != null){
                myStack.push(node.rightPlace);
            }
            //如果右节点不为空就压入
            if(node.leftPlace != null){
                myStack.push(node.leftPlace);
            }
            //如果左节点不为空就压入
        }
        //左节点后压入，左节点后出
    }

BFS 和 DFS 源代码

package DataStructure.FS;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class PlaceBFS {
    public static void main(String[] args) {
        PlaceTree szf = new PlaceTree("双子峰");
        PlaceTree aqdd = new PlaceTree("阿奇大道");
        PlaceTree syj = new PlaceTree("商业街");
        PlaceTree llw = new PlaceTree("牛罗湾");
        PlaceTree xyg = new PlaceTree("新宇港");
        PlaceTree kklj = new PlaceTree("酷客老街");
        PlaceTree jmdq = new PlaceTree("金门大桥");
        //创建节点
        szf.leftPlace = aqdd;
        szf.rightPlace = syj;
        aqdd.rightPlace = llw;
        syj.leftPlace = xyg;
        syj.rightPlace = kklj;
        xyg.rightPlace = llw;
        kklj.rightPlace = llw;
        llw.rightPlace = jmdq;
        //设置关系

        System.out.println("广度优先遍历结果:");
        new PlaceBFS().BroadFirstSearch(szf);
        System.out.println();
        System.out.println("深度优先遍历结果:");
        new PlaceBFS().DepthFirstSearch(szf);
    }

    public void BroadFirstSearch(PlaceTree nodeHead){
        //如果节点为空，返回
        if(nodeHead == null)
            return;
        //以队列的方式 (FIFO) 实现广度搜索
        Queue<PlaceTree> myQueue = new LinkedList<>();
        myQueue.add(nodeHead);
        //将节点压入队列
        while(! myQueue.isEmpty()){
            PlaceTree node = myQueue.poll();
                System.out.print(node.place + " ");
                if (null != node.leftPlace) {
                    myQueue.add(node.leftPlace);
                    //有左孩子就压左孩子
                }
                if (null != node.rightPlace) {
                    myQueue.add(node.rightPlace);
                    //有右孩子就压有孩子
                }
                //呈现左孩子和右孩子都压入队列中的情况，这样说好恐怖。
        }
    }

    public void DepthFirstSearch(PlaceTree nodeHead){
        if(nodeHead == null){
            return;
        }
        //以堆栈 (LIFO) 实现深度搜索
        Stack<PlaceTree> myStack = new Stack<>();
        myStack.add(nodeHead);
        while(! myStack.isEmpty()){
            PlaceTree node = myStack.pop();
            System.out.print(node.place+" ");
            if(node.rightPlace != null){
                myStack.push(node.rightPlace);
            }
            //如果右节点不为空就压入
            if(node.leftPlace != null){
                myStack.push(node.leftPlace);
            }
            //如果左节点不为空就压入
        }
        //左节点后压入，左节点后出
    }
}

结果

广度优先遍历结果:
双子峰 阿奇大道 商业街 牛罗湾 新宇港 酷客老街 金门大桥 牛罗湾 牛罗湾 金门大桥 金门大桥
深度优先遍历结果:
双子峰 阿奇大道 牛罗湾 金门大桥 商业街 新宇港 牛罗湾 金门大桥 酷客老街 牛罗湾 金门大桥

BFS 和 DFS 搜索方式

为什么深度优先搜索的结果更好，下图分析:

BFS的搜索步骤图

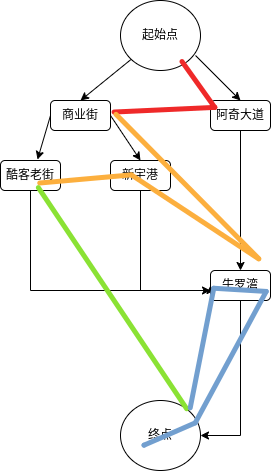
BFS 有点像横向的分层。

“起点”、“商业街”和“阿奇大道”为一层，

“酷客老街”、“新宇港”和“牛罗湾”为第二层，

“牛罗湾”和“终点”为第三次层，“终点”为第四层。

DFS的搜搜步骤图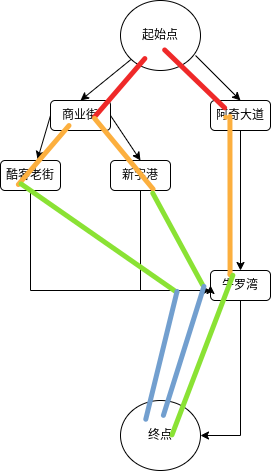

DFS 有点向竖向的分列。

“起点”、“阿奇大道”、“牛罗湾”、“终点” 为一列，得到最短解。

"起点"、“商业街”、“新宇港”、“牛罗湾”、“终点”为一列，得到第二种解。

“商业街”、“酷客老街”、“牛罗湾”、“终点”为一列，得到第三种解。