毕设(3)—机械臂工作空间

目录

• 毕设(3)—机械臂工作空间
  • 工作空间介绍
  • 图解法求工作空间
  • 数值法求工作空间（蒙特卡洛）
  • Matlab代码验证

毕设中用到了很多代码，其中一部分我通过看书和看论文学习并实现的代码，会通过Gitee仓库分享出来，这些代码仅用于学习使用，祝各位毕业生顺利完成毕设！

毕设系列内容：毕业设计——四自由度机械臂轨迹规划

---

毕设(3)—机械臂工作空间 工作空间介绍

工作空间指的是在进行实际作业时机械臂末端所能到达的所有空间点的集合，在机械臂的运动控制和轨迹规划都会考虑机械臂的工作空间。
工作空间常用的方法大致有3种，分别是解析法、图解法、数值法。解析法时利用数学方程描述机械臂的工作空间，这种方法直观性很差，只适用于结构简单的机械臂；图解法是求工作空间的剖面和剖线，这种方法便于观察，结构复杂的机械臂用图解法会很繁琐；数值法是用工具，通过机械臂的关节角度限制求末端的位置点，用尽可能多的点来模拟工作空间。

项目所使用的是四自由度机械臂，结构较为简单，所以本文采用图解法和数值法分别求解工作空间。

图解法求工作空间

在正逆运动学分析章节中得知机械臂的第四关节始终保持水平，所以图解法中可以用2、3关节来求得工作空间

已知机械臂DH参数表

i \(\alpha_{i-1}\) \(a_{i-1}\) \(d_i\) \(\theta_i\) \(\theta\)范围 1 0° 0 0 \(\theta_1\) (-90°~90°) 2 -90° 0 0 \(\theta_2\) (-85°~0°) 3 0° 135 0 \(\theta_3\) (-10°~95°) 4 0° 147 0 \(\theta_4\) \(-(\theta_2+\theta_3)\) 5 -90° 61 131 \(\theta_5\) (-90°~90°)

机械臂第2、3关节之间的角度如下图所示

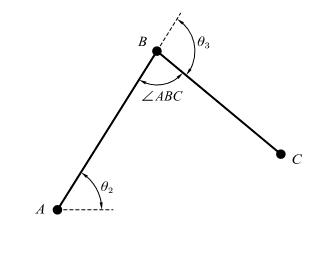
测量机械臂实体，得知\(\angle{ABC}\in[20,160]\)

结合\(\theta_2\)和\(\theta_3\)的角度范围，可以得到以下图形

我用sw做的简图

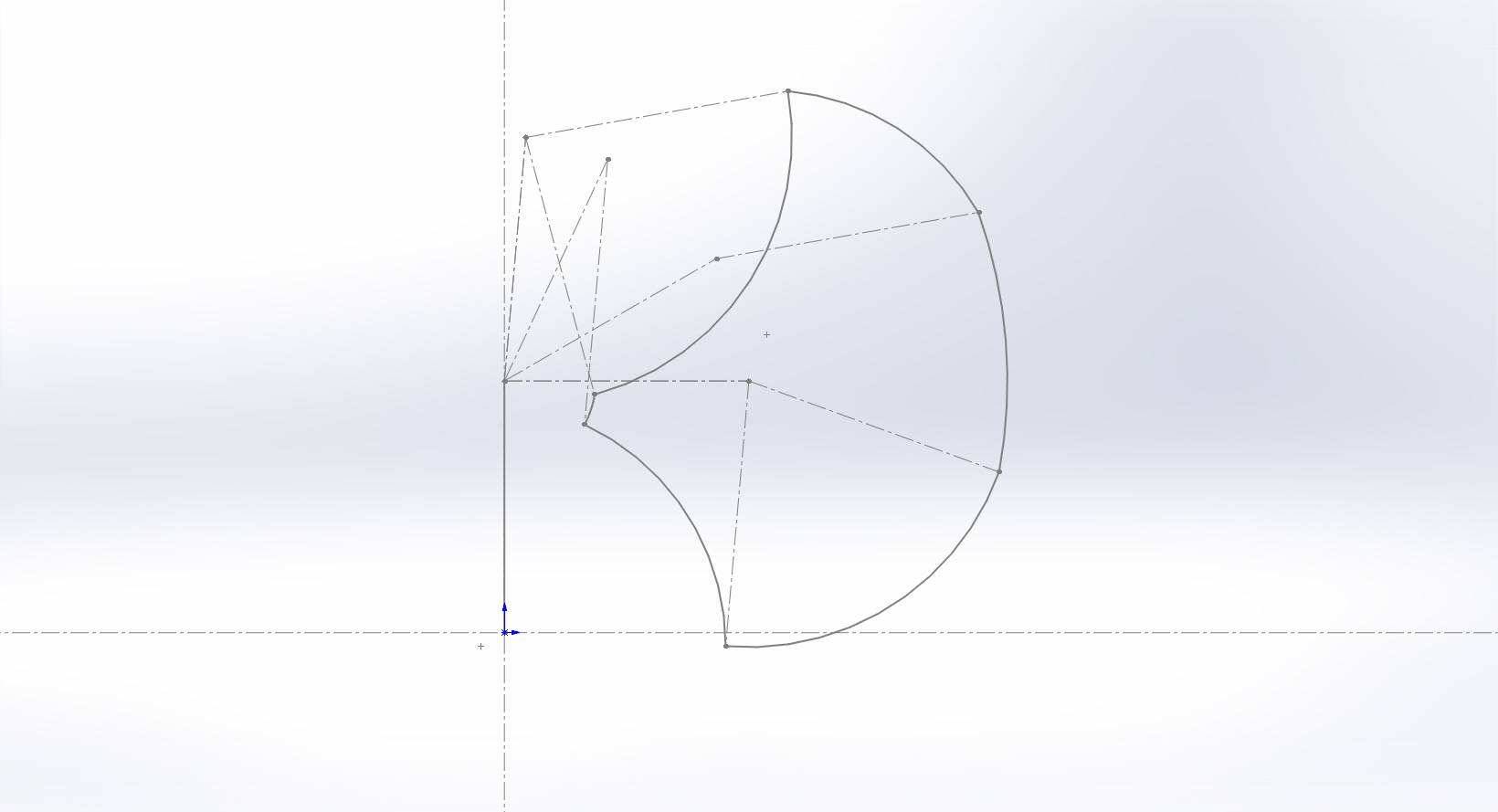
图中各个关键位置点都有连杆的展示，就不详细解释各个点了~

数值法求工作空间（蒙特卡洛）

数值法中最经典的方法就是蒙特卡洛法，

所用到的各关节角度范围在DH表中均有提及

由正逆运动学分析章节可知\(p_x\)、\(p_y\)、\(p_z\)的取值如下

\[\left\{ \begin{array}{l} p_x=c_1(c_{23}a_3+c_2a_2+a_4) \\ p_y=s_1(c_{23}a_3+c_2a_2+a_4) \\ p_z=-d_5-s_{23}a_3-s_2a_2 \end{array} \right. \]

Matlab代码验证

蒙特卡洛法求解工作空间的代码如下

clear; clc; close all;
N = 100000; %点集个数
a2 = 135; a3 = 147; a4 = 61; d5 = 131;
%定义矩阵
px1 = zeros(N, 1);
px2 = zeros(N, 1);
py = zeros(N, 1);
pz = zeros(N, 1);
%定义角度范围
limmin1 = -90.0;
limmax1 = 90.0;
limmin2 = -85.0;
limmax2 = 0.0;
limmin23 = -10.0;
limmax23 = 95.0;
%生成随机角度序列
theta1_1 = zeros(N, 1);
theta1_2 = (limmin1 + (limmax1 - limmin1) * rand(N, 1)) * pi / 180;
theta2 = (limmin2 + (limmax2 - limmin2) * rand(N, 1)) * pi / 180;
theta23 = (limmin23 + (limmax23 - limmin23) * rand(N, 1)) * pi / 180;

%角度位姿矩阵
for i = 1:N
    px1(i, 1) = cos(theta1_1(i)) * (cos(theta23(i)) * a3 + cos(theta2(i)) * a2 + a4);
    px2(i, 1) = cos(theta1_2(i)) * (cos(theta23(i)) * a3 + cos(theta2(i)) * a2 + a4);
    py(i, 1) = sin(theta1_2(i)) * (cos(theta23(i)) * a3 + cos(theta2(i)) * a2 + a4);
    pz(i, 1) =- (d5 + sin(theta23(i)) * a3 + sin(theta2(i)) * a2);
end

%工作空间图
figure(1);
plot3(px2, py, pz, 'b.', 'MarkerSize', 4);
title('工作空间图');
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
grid on;

%XY平面截图
figure(2);
plot(px2, py, 'b.', 'MarkerSize', 1.0);
title('XY平面截图');
xlabel('X轴');
ylabel('Y轴');
grid on;

%XZ平面截图
figure(3);
plot(px1, pz, 'b.', 'MarkerSize', 1.0);
title('XZ平面截图');
xlabel('X轴');
ylabel('Z轴');
grid on;

运行结果如下图

工作空间图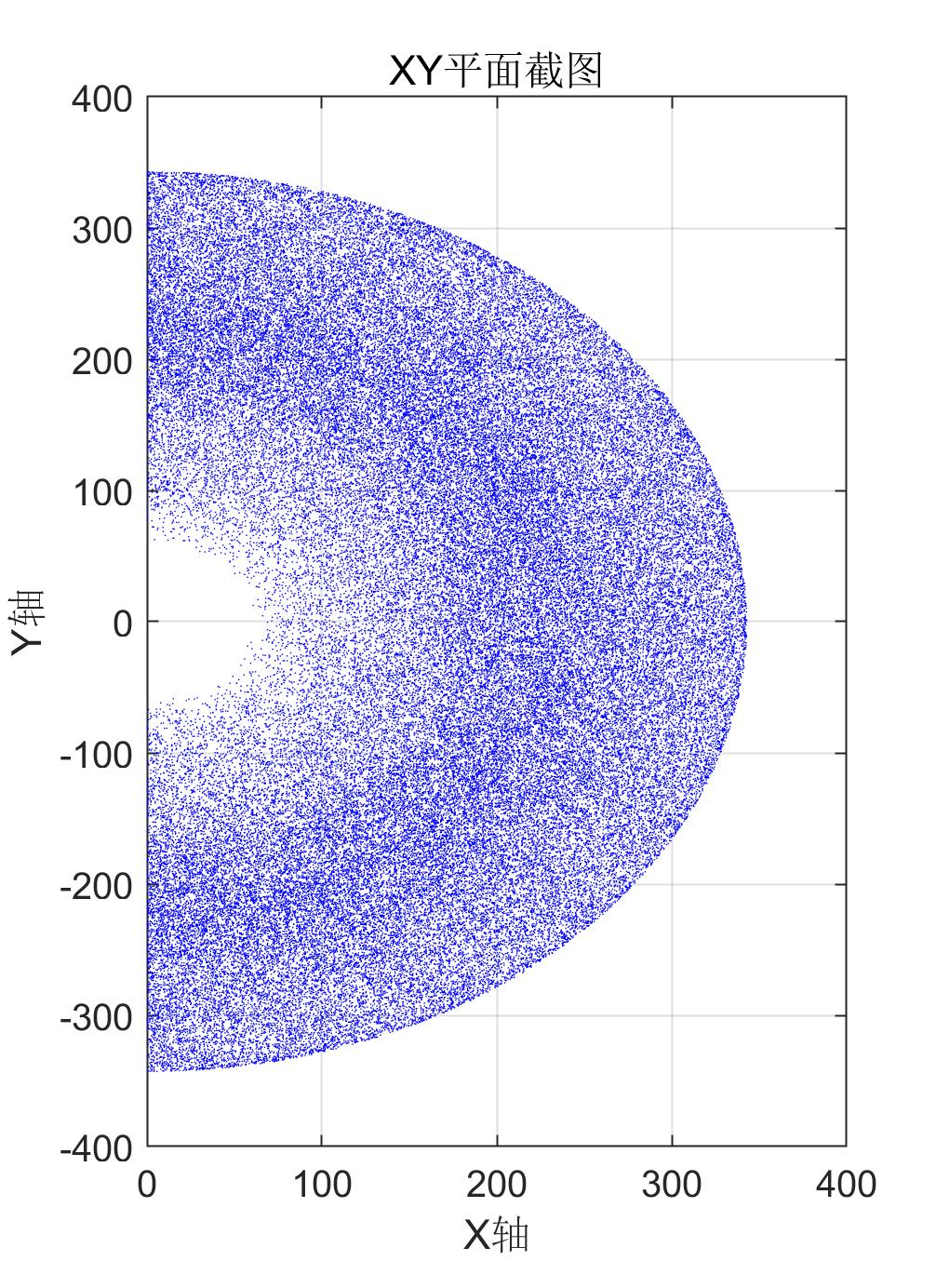 XY平面截图 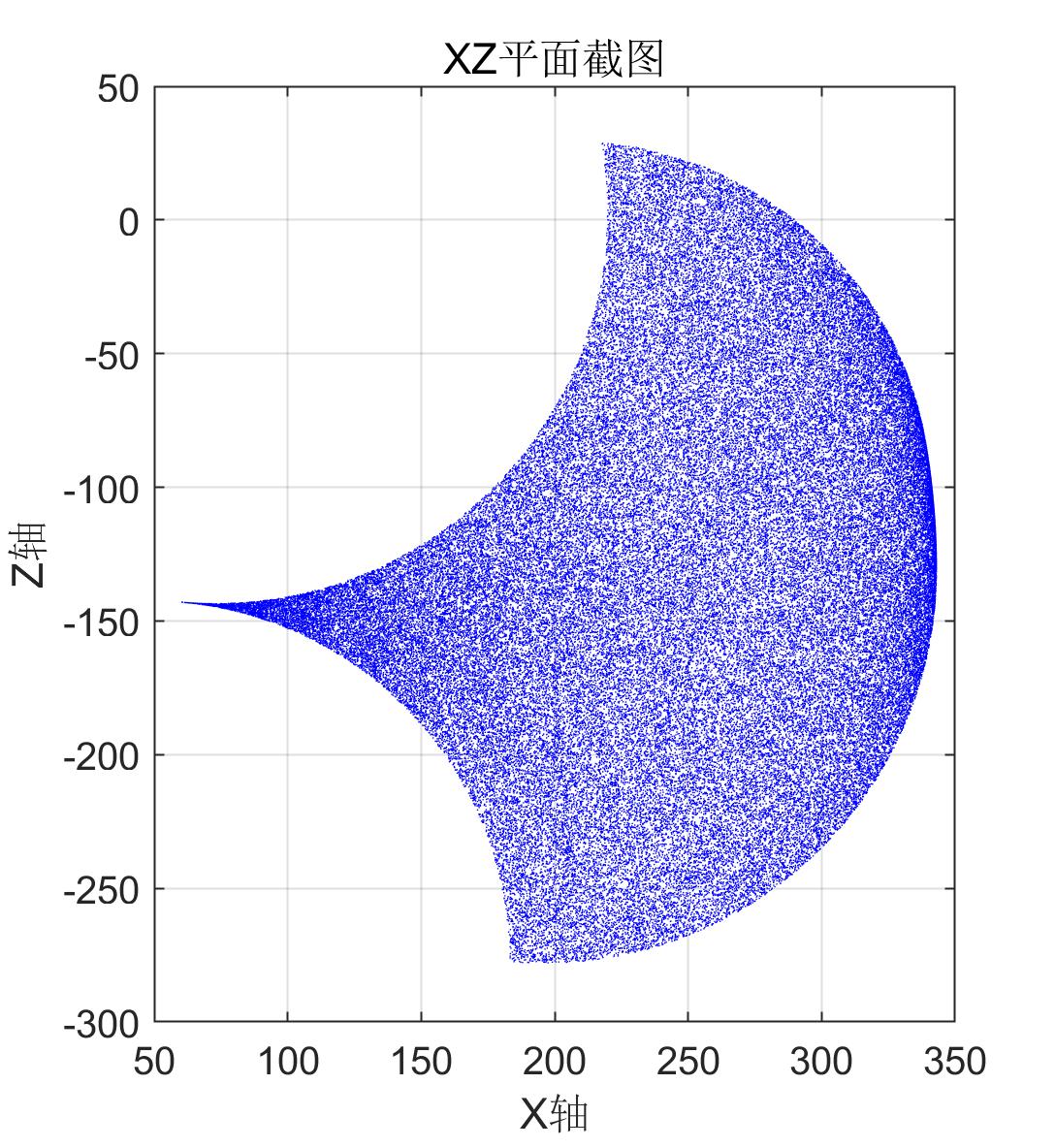XZ平面截图

本文到此结束，后续会继续更新的~