目前对图算法进行并行化的主要思想是将大图切分为多个子图，然后将这些子图分布到不同的机器上进行并行计算，在必要时进行跨机器通信同步计算得出结果。学术界和工业界提出了多种将大图切分为子图的划分方法，主要包括两种，边划分(Edge Cut)和点划分(Vertex Cut)。总而言之，边划分将节点分布到不同机器中(可能划分不平衡)，而点划分将边分布到不同机器中(划分较为平衡)。接下来我们使用的算法为边划分。我们下面的算法是简化版，没有处理悬挂节点的问题。
1. PageRank的两种串行迭代求解算法
我们在博客《数值分析：幂迭代和PageRank算法(Numpy实现)》算法中提到过用幂法求解PageRank。
给定有向图
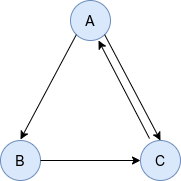
我们可以写出其马尔科夫概率转移矩阵\(M\)(第\(i\)列对应对\(i\)节点的邻居并沿列归一化)
\[\left(\begin{array}{lll} 0 & 0 & 1 \\ \frac{1}{2} & 0 & 0 \\ \frac{1}{2} & 1 & 0 \end{array}\right) \]然后我们定义Google矩阵为
\[G=\frac{q}{n} E+(1-q) M \]此处\(q\)为上网者从一个页面转移到另一个随机页面的概率（一般为0.15），\(1-q\) 为点击当前页面上链接的概率，\(E\)为元素全1的\(n\times n\) 矩阵( \(n\) 为节点个数)。
而PageRank算法可以视为求解Google矩阵占优特征值（对于随机矩阵而言，即1）对应的特征向量。设初始化Rank向量为 \(x\)（ \(x_i\) 为页面\(i\)的Rank值），则我们可以采用幂法来求解：
\[x_{t+1}=G x_{t} \](每轮迭代后要归一化)
现实场景下的图大多是稀疏图，即\(M\)是稀疏矩阵。幂法中计算 \((1-q)Mx_t\) ，对于节点 \(i\) 需使用reduceByKey()（key为节点编号）操作。计算 \(\frac{q}{n}{E}x_t\) 则需要对所有节点的Rank进行reduce()操作，操作颇为繁复。
PageRank还有一种求解算法（名字就叫“迭代算法”），它的迭代形式如下：
\[x_{t+1} = \frac{q}{n}\bm{1} + (1-q)Mx_t \]可以看到，这种迭代方法就规避了计算 \(\frac{q}{n}Ex_t\)，通信开销更小。我们接下来就采用这种迭代形式。
2. 图划分的两种方法目前对图算法进行并行化的主要思想是将大图切分为多个子图，然后将这些子图分布到不同的机器上进行并行计算，在必要时进行跨机器通信同步计算得出结果。学术界和工业界提出了多种将大图切分为子图的划分方法，主要包括两种，边划分(Edge Cut)和点划分(Vertex Cut)。
2.1 边划分如下图所示，边划分是对图中某些边进行切分。具体在Pregel[1]图计算框架中，每个分区包含一些节点和节点的出边；在GraphLab[2]图计算框架中，每个分区包含一些节点、节点的出边和入边，以及这些节点的邻居节点。边划分的优点是可以保留节点的邻居信息，缺点是容易出现划分不平衡，如对于度很高的节点，其关联的边都被划分到一个分区中，造成其他分区中的边可能很少。另外，如下图最右边的图所示，边划分可能存在边冗余。
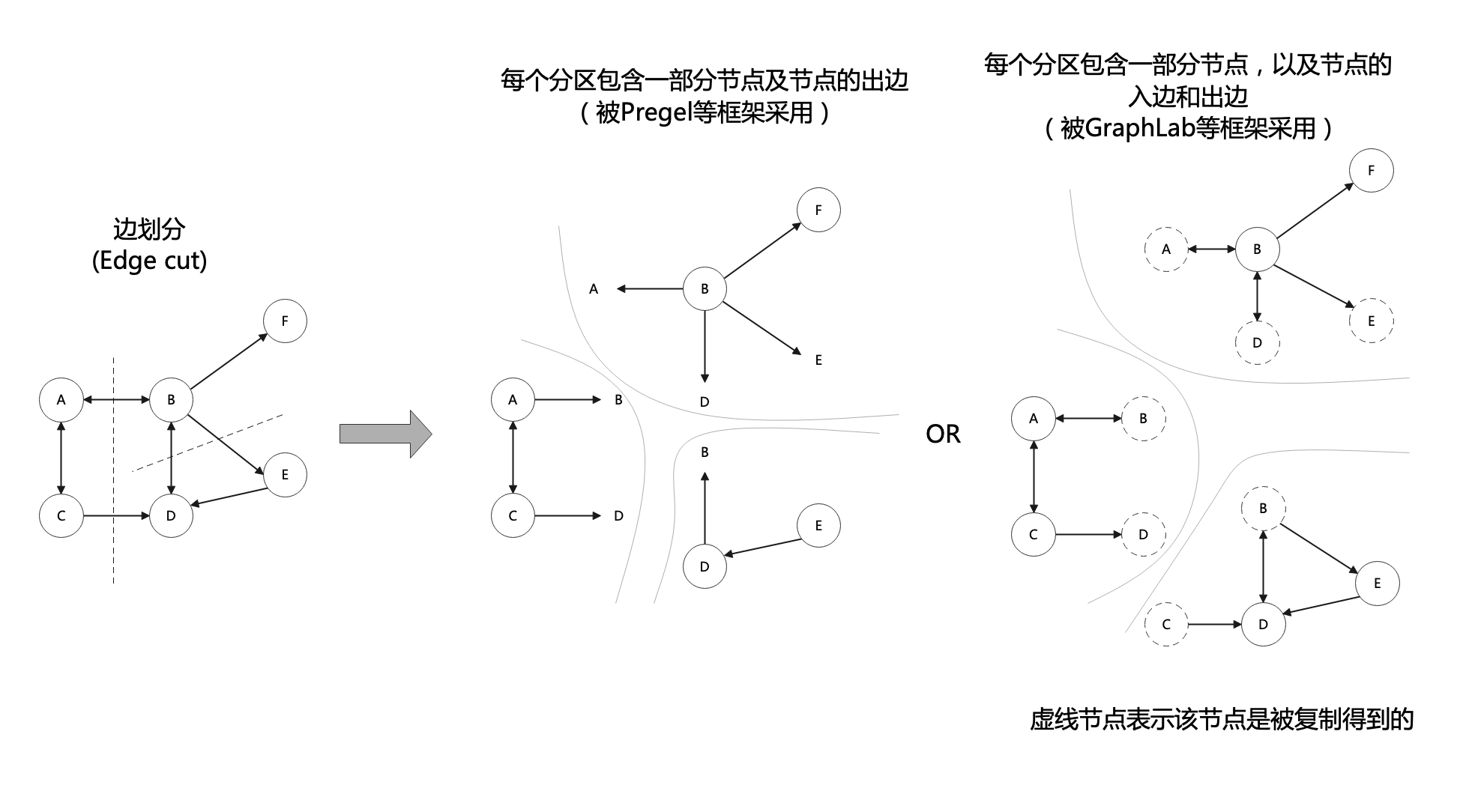2.2 点划分
如下图所示，点划分是对图中某些点进行切分，得到多个图分区，每个分区包含一部分边，以及与边相关联的节点。具体地，PowerGraph[3]，GraphX[4]等框架采用点划分，被划分的节点存在多个分区中。点划分的优缺点与边划分的优缺点正好相反，可以将边较为平均地分配到不同机器中，但没有保留节点的邻居关系。
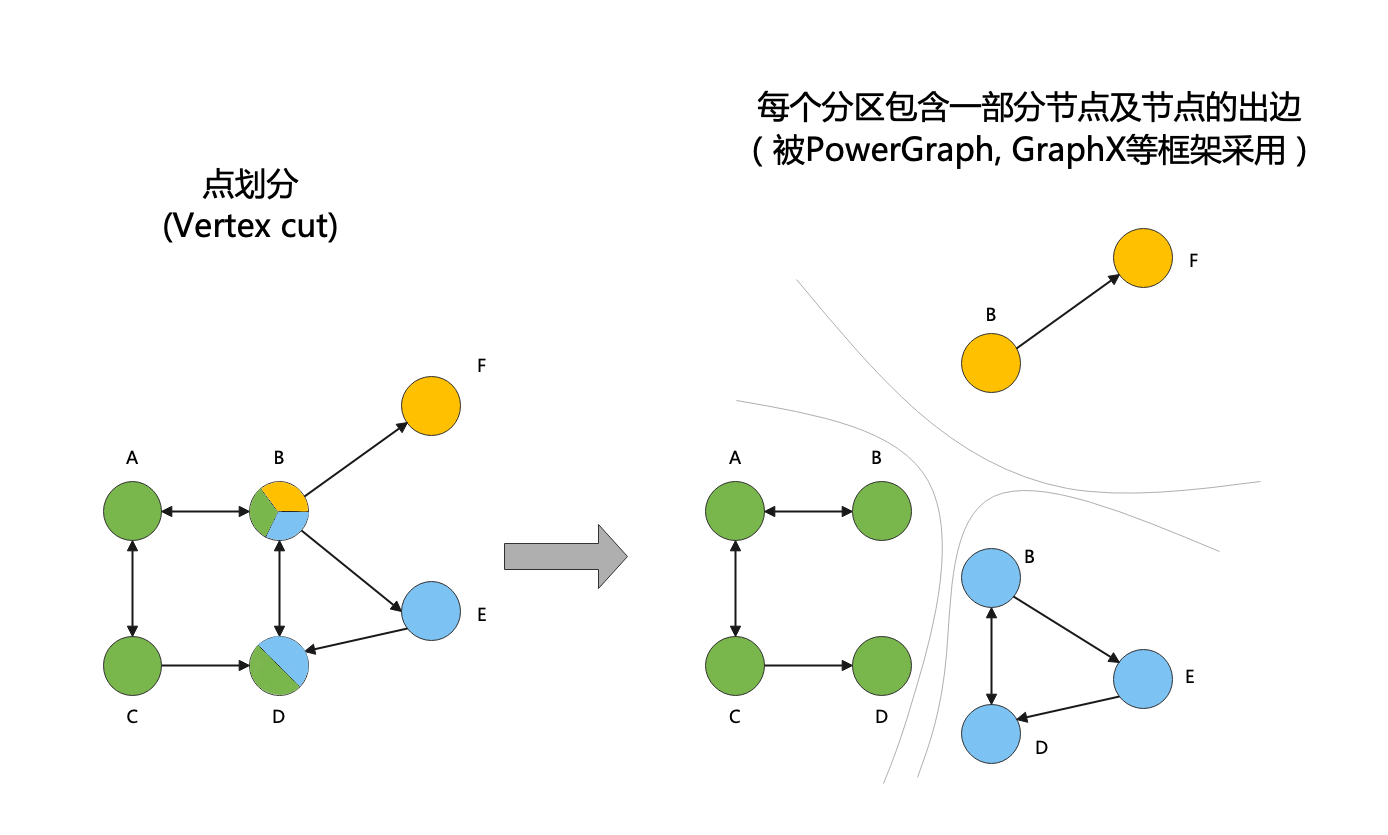
总而言之，边划分将节点分布到不同机器中(可能划分不平衡)，而点划分将边分布到不同机器中(划分较为平衡)。接下来我们使用的算法为类似Pregel的划分方式，使用边划分。我们下面的算法是简化版，没有处理悬挂节点的问题。
3. 对迭代算法的并行化我们将Rank向量用均匀分布初始化（也可以用全1初始化，不过就不再以概率分布的形式呈现），设分区数为3，算法总体迭代流程可以表示如下：
注意，图中flatMap()步骤中，节点\(i\)计算其contribution（贡献度）：\((x_t)_i/|\mathcal{N}_i|\)，并将贡献度发送到邻居集合\(\mathcal{N}_i\)中的每一个节点。之后，将所有节点收到的贡献度使用reduceByKey()（节点编号为key）规约后得到向量\(\hat{x}\)，和串行算法中\(Mx_t\)的对应关系如下图所示：
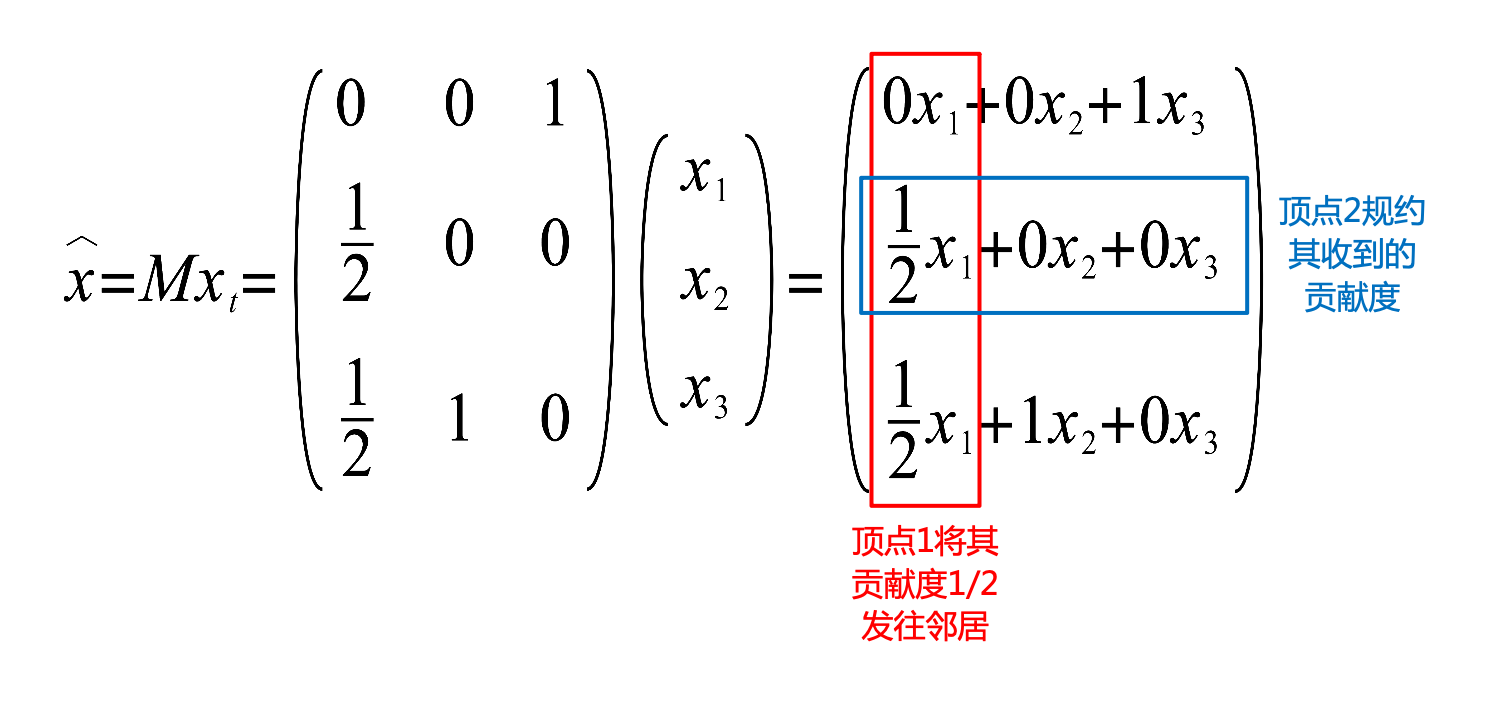
并按照公式\(x_{t+1} = \frac{q}{n} + (1-q)\hat{x}\)来计算节点的Rank向量。然后继续下一轮的迭代过程。
4. 编程实现用PySpark对PageRank进行并行化编程实现，代码如下：
import re
import sys
from operator import add
from typing import Iterable, Tuple
from pyspark.resultiterable import ResultIterable
from pyspark.sql import SparkSession
n_slices = 3 # Number of Slices
n_iterations = 10 # Number of iterations
q = 0.15 #the default value of q is 0.15
def computeContribs(neighbors: ResultIterable[int], rank: float) -> Iterable[Tuple[int, float]]:
# Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
num_neighbors = len(neighbors)
for vertex in neighbors:
yield (vertex, rank / num_neighbors)
if __name__ == "__main__":
# Initialize the spark context.
spark = SparkSession\
.builder\
.appName("PythonPageRank")\
.getOrCreate()
# link: (source_id, dest_id)
links = spark.sparkContext.parallelize(
[(1, 2), (1, 3), (2, 3), (3, 1)],
n_slices
)
# drop duplicate links and convert links to an adjacency list.
adj_list = links.distinct().groupByKey().cache()
# count the number of vertexes
n_vertexes = adj_list.count()
# init the rank of each vertex, the default is 1.0/n_vertexes
ranks = adj_list.map(lambda vertex_neighbors: (vertex_neighbors[0], 1.0/n_vertexes))
# Calculates and updates vertex ranks continuously using PageRank algorithm.
for t in range(n_iterations):
# Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
contribs = adj_list.join(ranks).flatMap(lambda vertex_neighbors_rank: computeContribs(
vertex_neighbors_rank[1][0], vertex_neighbors_rank[1][1] # type: ignore[arg-type]
))
# Re-calculates rank of each vertex based on the contributions it received
ranks = contribs.reduceByKey(add).mapValues(lambda rank: q/n_vertexes + (1 - q)*rank)
# Collects all ranks of vertexs and dump them to console.
for (vertex, rank) in ranks.collect():
print("%s has rank: %s." % (vertex, rank))
spark.stop()
运行结果如下：
1 has rank: 0.38891305880091237.
2 has rank: 0.214416470596171.
3 has rank: 0.3966704706029163.
该Rank向量与我们采用串行幂法得到的Rank向量 \(R=(0.38779177,0.21480614,0.39740209)^{T}\) 近似相等，说明我们的并行化算法运行正确。
参考-
[1] Malewicz G, Austern M H, Bik A J C, et al. Pregel: a system for large-scale graph processing[C]//Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. 2010: 135-146.
-
[2] Low Y, Gonzalez J, Kyrola A, et al. Distributed graphlab: A framework for machine learning in the cloud[J]. arXiv preprint arXiv:1204.6078, 2012.
-
[3] Gonzalez J E, Low Y, Gu H, et al. {PowerGraph}: Distributed {Graph-Parallel} Computation on Natural Graphs[C]//10th USENIX symposium on operating systems design and implementation (OSDI 12). 2012: 17-30.
-
[4] Spark: GraphX Programming Guide
-
[5] GiHub: Spark官方Python样例
-
[6] 许利杰，方亚芬. 大数据处理框架Apache Spark设计与实现[M]. 电子工业出版社, 2021.
-
[7] Stanford CME 323: Distributed Algorithms and Optimization (Lecture 15)
-
[8] wikipedia: PageRank
-
[9] 李航. 统计学习方法(第2版)[M]. 清华大学出版社, 2019.
-
[10] Timothy sauer. 数值分析(第2版)[M].机械工业出版社, 2018.