决策树的概念 略
熵和基尼指数 信息增益信息增益 information gain 是用于训练决策树的指标。具体来说,是指这些指标衡量拆分的质量。通俗来说是通过根据随机变量的给定值拆分数据集来衡量熵。
通过描述一个事件是否"惊讶",通常低概率事件更令人惊讶,因此具有更大的信息量。而具有相同可能性的事件的概率分布更"惊讶"并且具有更大的熵。
定义:熵 entropy是一组例子中杂质、无序或不确定性的度量。熵控制决策树如何决定拆分数据。它实际上影响了决策树如何绘制边界。
熵熵的计算公式为:\(E=-\sum^i_{i=1}(p_i\times\log_2(p_i))\) ;\(P_i\) 是类别 \(i\) 的概率。我们来举一个例子来更好地理解熵及其计算。假设有一个由三种颜色组成的数据集,红色、紫色和黄色。如果我们的集合中有一个红色、三个紫色和四个黄色的观测值,我们的方程变为:\(E=-(p_r \times \log_2(p_r) + p_p \times \log_2(p_p) + p_y \times \log_2(p_y)\)
其中 \(p_r\) 、\(p_p\) 和 \(p_y\) 分别是选择红色、紫色和黄色的概率。假设 \(p_r=\frac{1}{8}\),\(p_p=\frac{3}{8}\) ,\(p_y=\frac{4}{8}\) 现在等式变为变为:
- \(E=-(\frac{1}{8} \times \log_2(\frac{1}{8}) + \frac{3}{8} \times \log_2(\frac{3}{8}) + \frac{4}{8} \times \log_2(\frac{4}{8}))\)
- $0.125 \times log_2(0.125) + 0.375 \times log_2(0.375) + 0.5 \times log_2(0.375) $
- \(0.125 \times -3 + 0.375 \times -1.415 + 0.5 \times -1 = -0.375+-0.425 +-0.5 = 1.41\)
当所有观测值都属于同一类时会发生什么? 在这种情况下,熵将始终为零。\(E=-(1log_21)=0\) ;这种情况下的数据集没有杂质,这就意味着没有数据集没有意义。又如果有两类数据集,一半是黄色,一半是紫色,那么熵为1,推导过程是:\(E=−(\ (0.5\log_2(0.5))+(0.5\times \log_2(0.5))\ ) = 1\)
基尼指数基尼指数 Gini index 和熵 entropy 是计算信息增益的标准。决策树算法使用信息增益来拆分节点。
基尼指数计算特定变量在随机选择时被错误分类的概率程度以及基尼系数的变化。它适用于分类变量,提供“成功”或“失败”的结果,因此仅进行二元拆分(二叉树结构)。基尼指数在 0 和 1 之间变化,其中,1 表示元素在各个类别中的随机分布。基尼指数为 0.5 表示元素在某些类别中分布均匀。:
- 0 表示为所有元素都与某个类相关联,或只存在一个类。
- 1 表示所有元素随机分布在各个类中,并且0.5 表示元素均匀分布到某些类中
基尼指数公式:\(1− \sum_n^{i=1}(p_i)^2\) ; \(P_i\) 为分类到特定类别的概率。在构建决策树时,更愿意选择具有最小基尼指数的属性作为根节点。
通过实例了解公式
计算基尼指数
已知条件
-
\(P(Past\ Trend=Positive) = \frac{6}{10}\)
-
\(P(Past\ Trend=Negative) = \frac{4}{10}\)
过去趋势基尼指数计算
如果过去趋势为正面,回报为上涨,概率为:\(P(Past\ Trend=Positive\ \&\ Return=Up) = \frac{4}{6}\)
如果过去趋势为正面,回报为下降,概率为:\(P(Past\ Trend=Positive\ \&\ Return=Down) = \frac{2}{6}\)
- 那么这个基尼指数为:\(gini(Past\ Trend) = 1-(\frac{4}{6}^2+\frac{2}{6}^2) = 0.45\)
如果过去趋势为负面,回报为上涨,概率为:\(P(Past\ Trend=Negative\ \&\ Return=Up) = 0\)
如果过去趋势为负面,回报为下降,概率为:\(P(Past\ Trend=Negative\ \&\ Return=Down) = \frac{4}{4}\)
- 那么这个基尼指数为:\(gini(Past\ Trend=Negative) = 1-(0^2+\frac{4}{4}^2) = 1-(0+1)=0\)
那么过去交易量的的基尼指数加权 = \(\frac{6}{10} \times 0.45 + \frac{4}{10}\times 0 = 0.27\)
未平仓量基尼指数计算
已知条件
- \(P(Open\ Interest=High): \frac{4}{10}\)
- \(P(Open\ Interest=Low): \frac{6}{10}\)
如果未平仓量为 high 并且回报为上涨,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Up)=\frac{2}{4}\)
如果未平仓量为 high 并且回报为下降,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Down)=\frac{2}{4}\)
- 那么这个基尼指数为:\(gini(Open\ Interest=High) = 1-(\frac{2}{4}^2+\frac{2}{4}^2) = 0.5\)
如果未平仓量为 low 并且回报为上涨,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Up)=\frac{2}{6}\)
如果未平仓量为 low 并且回报为下降,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Down)=\frac{4}{6}\)
- 那么这个基尼指数为:\(gini(Open\ Interest=Low) = 1-(\frac{2}{6}^2+\frac{4}{6}^2) = 0.45\)
那么未平仓量基尼指数加权 = \(\frac{4}{10} \times 0.5 + \frac{6}{10}\times 0.45 = 0.47\)
计算交易量基尼指数
已知条件
- \(P(Trading\ Volume=High): \frac{7}{10}\)
- \(P(Trading\ Volume=Low): \frac{3}{10}\)
如果交易量为 high 并且回报为上涨,概率为:\(P(Trading\ Volume=High\ \&\ Return\ = Up)=\frac{4}{7}\)
如果交易量为 high 并且回报为下降,概率为:\(P(Trading\ Volume = High\ \&\ Return\ = Down)=\frac{3}{7}\)
- 那么这个基尼指数为:\(gini(Trading\ Volume=High) = 1-(\frac{4}{7}^2+\frac{3}{7}^2) = 0.49\)
如果交易量为 low 并且回报为上涨,概率为:\(P(Trading\ Volume = Low\ \&\ Return\ = Up)=0\)
如果交易量为 low 并且回报为下降,概率为:\(P(Trading\ Volume = Low\ \&\ Return\ = Down)=\frac{3}{3}\)
- 那么这个基尼指数为:\(gini(Trading\ Volume=Low) = 1-(0^2+1^2) = 0\)
那么交易量基尼指数加权 = \(\frac{7}{10} \times 0.49 + \frac{3}{10}\times 0 = 0.34\)
最终计算出的基尼指数列表如下,在表中可以观察到“Past Trend”的基尼指数最低,因此它将被选为决策树的根节点。
这里将重复的过程来确定决策树的子节点或分支。将通过计算”Past Trend“的“Positive”分支的基尼指数如下:
针对过去正面趋势计算未平仓量的基尼指数
已知条件
- \(P(Open\ Interest=High): \frac{2}{6}\)
- \(P(Open\ Interest=Low): \frac{4}{6}\)
如果未平仓量为 high 并且回报为上涨,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Up)=\frac{2}{2}\)
如果未平仓量为 high 并且回报为下降,概率为:\(P(Open\ Interest = High\ \&\ Return\ = Down)=0\)
- 那么这个基尼指数为:\(gini(Open\ Interest=High) = 1-(\frac{2}{2}^2+0^2) = 0\)
如果未平仓量为 low 并且回报为上涨,概率为:\(P(Open\ Interest = Low\ \&\ Return\ = Up)=\frac{2}{4}\)
如果未平仓量为 low 并且回报为下降,概率为:\(P(Open\ Interest = Low\ \&\ Return\ = Down)=\frac{2}{4}\)
- 那么这个基尼指数为:\(gini(Open\ Interest=Low) = 1-(\frac{2}{4}^2+\frac{2}{4}^2) = 0.5\)
那么未平仓量基尼指数加权 = \(\frac{2}{6} \times 0 + \frac{4}{6}\times 0.5 = 0.33\)
计算交易量基尼指数
已知条件
- \(P(Trading\ Volume=High): \frac{4}{6}\)
- \(P(Trading\ Volume=Low): \frac{2}{6}\)
如果交易量为 high 并且回报为上涨,概率为:\(P(Trading\ Volume=High\ \&\ Return\ = Up)=\frac{4}{4}\)
如果交易量为 high 并且回报为下降,概率为:\(P(Trading\ Volume = High\ \&\ Return\ = Down)=0\)
- 那么这个基尼指数为:\(gini(Trading\ Volume=High) = 1-(\frac{4}{4}^2+0^2) = 0\)
如果交易量为 low 并且回报为上涨,概率为:\(P(Trading\ Volume = Low\ \&\ Return\ = Up)=0\)
如果交易量为 low 并且回报为下降,概率为:\(P(Trading\ Volume = Low\ \&\ Return\ = Down)=\frac{2}{2}\)
- 那么这个基尼指数为:\(gini(Trading\ Volume=Low) = 1-(0^2+\frac{2}{2}^2) = 0\)
那么交易量基尼指数加权 = \(\frac{4}{6} \times 0 + \frac{2}{6}\times 0 = 0\)
最终计算出的基尼指数列表如下,这里将使用“Trading Volume”进一步拆分节点,因为它具有最小的基尼指数。
最终的模型就如图所示
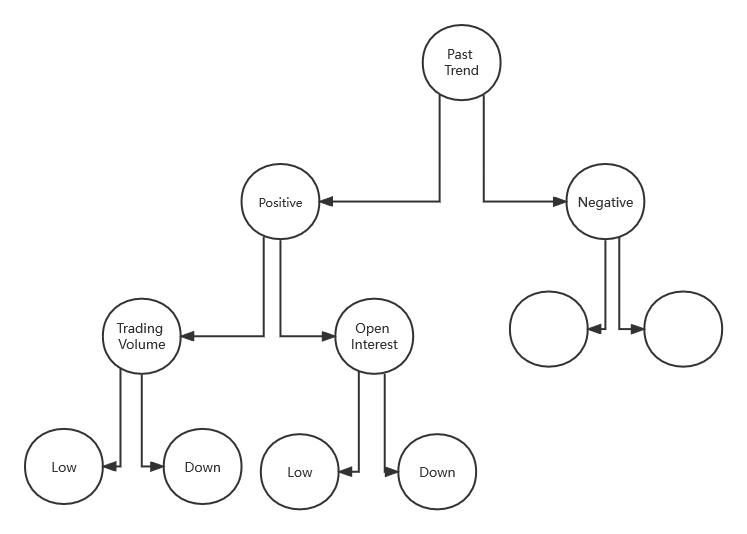
我们可以根据属于一类数据的概率分布来考虑数据集的熵,例如,在二进制分类数据集的情况下为两个类。计算样本的熵如 \(Entropy = -(P_0 \times log(P_0) + P_1 \times log(P_1)\) 。
两类的样本拆分为 50/50 的数据集将具最大熵(最惊讶),而拆分为 10/90 的不平衡数据集将具有较小的熵。可以通过在 Python 中计算这个不平衡数据集的熵的例子来证明这一点。
from math import log2
# 概率
class0 = 10/100
class1 = 90/100
# entropy formula
entropy = -(class0 * log2(class0) + class1 * log2(class1))
# print the result
print('entropy: %.3f bits' % entropy)
运行示例,可以看到用于二分类的数据集的熵小于 1 。也就是说,对来自数据集中的任意示例类进行编码所需的信息不到1。通过这种方式,熵可以用作数据集纯度的计算,例如类别分布的平衡程度。
熵为 0 位表示数据集包含一个类;1或更大位的熵表示平衡数据集的最大熵(取决于类别的数量),介于两者之间的值表示这些极端之间的水平。
计算信息增益示例要求:定义一个函数来根据属于 0 类和 1 类的样本的比率来计算一组样本的熵。
假设有一个20 个示例的数据集,13 个为0 类,7 个为1 类。我们可以计算该数据集的熵,它的熵小于 1 位。
from math import log2
# calculate the entropy for the split in the dataset
def entropy(class0, class1):
return -(class0 * log2(class0) + class1 * log2(class1))
# split of the main dataset
class0 = 13 / 20
class1 = 7 / 20
# calculate entropy before the change
s_entropy = entropy(class0, class1)
print('Dataset Entropy: %.3f bits' % s_entropy)
# Dataset Entropy: 0.934 bits
假设按照 value1 分割数据集,有一组 8 个样本的数据集,7 个为第 0 类,1 个用于第 1 类。然后我们可以计算这组样本的熵。
from math import log2
# calculate the entropy for the split in the dataset
def entropy(class0, class1):
return -(class0 * log2(class0) + class1 * log2(class1))
# split of the main dataset
s1_class0 = 7 / 8
s1_class1 = 1 / 8
# calculate entropy before the change
s_entropy = entropy(s1_class0, s1_class1)
print('Dataset Entropy: %.3f bits' % s_entropy)
# Dataset Entropy: 0.544 bits
假设现在按 value2 分割数据集;一组 12 个样本数据集,每组 6 个。我们希望这个组的熵为 1。
from math import log2
# calculate the entropy for the split in the dataset
def entropy(class0, class1):
return -(class0 * log2(class0) + class1 * log2(class1))
# split of the main dataset
s1_class0 = 6 / 12
s1_class1 = 6 / 12
# calculate entropy before the change
s_entropy = entropy(s1_class0, s1_class1)
print('Dataset Entropy: %.3f bits' % s_entropy)
# Dataset Entropy: 1.000 bits
最后,可以根据为变量的每个值创建的组和计算的熵来计算该变量的信息增益。例如:
第一个变量从数据集中产生一组 8 个样本,第二组在数据集中有12 个样本。在这种情况下,信息增益计算:
- \(Entropy(Dataset) – (\frac{(Count(Group1)}{Count(Dataset)} \times Entropy(Group1) + \frac{Count(Group2)}{Count(Dataset)} \times Entropy(Group2)))\)
这里是因为在每个子节点重复这个分裂过程直到空叶节点。这意味着每个节点的样本都属于同一类。但是,这种情况下会导致具有许多节点使非常深的树,这很容易导致过度拟合。因此,我们通常希望通过设置树的最大深度来修剪树。IG就是我们想确定给定训练特征向的量集中的哪个属性最有用,那么上面的公式推理就为:
- \(IG(D_p) = I(D_p) − \frac{N_{left}}{N_p}I(D_{left})−\frac{N_{right}}{N_p}I(D_{right})\)
- \(IG(D_P)\):数据集的信息增益
- \(I(D)\):叶子的熵或基尼指数
- \(\frac{N}{N_P}\) :页数据集占总数据集的比例
我们将使用它来决定决策树 节点中属性的顺序。该行为在python中表示为:
from math import log2
# calculate the entropy for the split in the dataset
def entropy(class0, class1):
return -(class0 * log2(class0) + class1 * log2(class1))
# split of the main dataset
class0 = 13 / 20
class1 = 7 / 20
# calculate entropy before the change
s_entropy = entropy(class0, class1)
print('Dataset Entropy: %.3f bits' % s_entropy)
# split 1 (split via value1)
s1_class0 = 7 / 8
s1_class1 = 1 / 8
# calculate the entropy of the first group
s1_entropy = entropy(s1_class0, s1_class1)
print('Group1 Entropy: %.3f bits' % s1_entropy)
# split 2 (split via value2)
s2_class0 = 6 / 12
s2_class1 = 6 / 12
# calculate the entropy of the second group
s2_entropy = entropy(s2_class0, s2_class1)
print('Group2 Entropy: %.3f bits' % s2_entropy)
# calculate the information gain
gain = s_entropy - (8/20 * s1_entropy + 12/20 * s2_entropy)
print('Information Gain: %.3f bits' % gain)
# Dataset Entropy: 0.934 bits
# Group1 Entropy: 0.544 bits
# Group2 Entropy: 1.000 bits
# Information Gain: 0.117 bits
通过实例,就可以很清楚的明白了,信息增益的概念:信息熵-条件熵,换句话来说就是信息增益代表了在一个条件下,信息复杂度(不确定性)减少的程度。
python计算决策树实例 基于基尼指数的决策树钞票数据集涉及根据从照片中采取的一系列措施来预测给定钞票是否是真实的。数据是取自真钞和伪钞样样本的图像中提取的。对于数字化,使用了通常用于印刷检查的工业相机,从图像中提取特征。
该数据集包含 1372 行和 5 个数值变量。这是一个二元分类的问题。
基尼指数假设有两组数据,每组有 2 行。第一组的行都属于 0 类,第二组的行都属于 1 类,所以这是一个完美的拆分。
首先需要计算每个组中类的比例。
proportion = count(class_value) / count(rows)
这个比例是
group_1_class_0 = 2 / 2 = 1
group_1_class_1 = 0 / 2 = 0
group_2_class_0 = 0 / 2 = 0
group_2_class_1 = 2 / 2 = 1
为每个子节点计算 Gini index
gini_index = sum(proportion * (1.0 - proportion))
gini_index = 1.0 - sum(proportion * proportion)
然后对每组的基尼指数按组的大小加权,例如当前正在分组的所有样本。我们可以将此权重添加到组的基尼指数计算中,如下所示:
gini_index = (1.0 - sum(proportion * proportion)) * (group_size/total_samples)
在该案例中,每个组的基尼指数为:
Gini(group_1) = (1 - (1*1 + 0*0)) * 2/4
Gini(group_1) = 0.0 * 0.5
Gini(group_1) = 0.0 # 分类1的基尼指数
Gini(group_2) = (1 - (0*0 + 1*1)) * 2/4
Gini(group_2) = 0.0 * 0.5
Gini(group_2) = 0.0 # 分类2的基尼指数
然后在分割点的每个子节点上添加分数,以给出分割点的最终 Gini 分数,该分数可以与其他候选分割点进行比较。如该分割点的基尼系数为 \(0.0 + 0.0\) 或完美的基尼系数 0.0。
编写一个 gini_index() 的函数,用于计算组列表和已知类值列表的基尼指数。
def gini_index(groups, classes):
print("------------")
# 计算所有样本的分割点,计算样本的总长度
n_instances = float(sum([len(group) for group in groups]))
# 计算每个组的总基尼指数
gini = 0.0
for group in groups:
size = float(len(group))
if size == 0: # avoid divide by zero
continue
score = 0.0
# score the group based on the score for each class
for class_val in classes:
# row[-1] 代表每个样本的最后一个值,是否存在分类 class_val
p = [row[-1] for row in group]
p1 = p.count(class_val) / size
score += p1 * p1
# 按照对应的样本分割点,加权重
gini += (1.0 - score) * (size / n_instances)
return gini
print(gini_index([[[1, 1], [1, 0]], [[1, 1], [1, 0]]], [0, 1]))
print(gini_index([[[1, 0], [1, 0]], [[1, 1], [1, 1]]], [0, 1]))
运行该示例会打印两组的Gini index,最差情况的为 0.5,最少情况的指数为 0.0。

拆分是由数据集中的一个属性和一个值组成。可以将其总结为要拆分的属性的索引和拆分该属性上的行的值。这只是索引数据行的有用简写。
创建拆分涉及三个部分,我们已经看过的第一个部分是计算基尼分数。剩下的两部分是:
- 拆分数据集。
- 评估所有拆分。
拆分数据是给定数据集索引和拆分值,将数据集拆分为两个行列表形成一个分类。具体是拆分数据集涉及遍历每一行,检查属性值是否低于或高于拆分值,并将其分别分配给左组或右组。当存在两个组时,可以按照基尼指数进行评估
编写一个test_split()函数,它实现了拆分。
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
给定一个数据集,必须检查每个属性上的每个值作为候选拆分,评估拆分的成本并找到我们可以进行的最佳拆分。一旦找到最佳值,就可以将其用作决策树中的节点。
这里使用 dict 作为决策树中的节点,因为这样可以按名称存储数据。选择最佳基尼指数并将其用作树的新节点。
每组数据都是其小数据集,其中仅包含通过拆分过程分配给左组或右组的那些行。可以想象我们如何在构建决策树时递归地再次拆分每个组。
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
之后准备一些测试数据集进行测试,其中 \(Y\) 是测试集的分类
X1 X2 Y
2.771244718 1.784783929 0
1.728571309 1.169761413 0
3.678319846 2.81281357 0
3.961043357 2.61995032 0
2.999208922 2.209014212 0
7.497545867 3.162953546 1
9.00220326 3.339047188 1
7.444542326 0.476683375 1
10.12493903 3.234550982 1
6.642287351 3.319983761 1
将上述代码整合为一起,运行该代码后会打印所有基尼指数,基尼指数为 0.0 或完美分割。
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculate the Gini index for a split dataset
def gini_index(groups, classes):
# 计算两组数据集的总数每个种类的列表数量和
n_instances = float(sum([len(group) for group in groups]))
# 计算每组的基尼值
gini = 0.0
for group in groups:
size = float(len(group))
# avoid divide by zero
if size == 0:
continue
score = 0.0
# score the group based on the score for each class
for class_val in classes:
# 拿出数据集中每行的类型,拆开是为了更好的了解结构
p = [row[-1] for row in group]
# print("%f / %f = %f" % (p.count(class_val), size, p.count(class_val) / size ))
# 这里计算的是当前的分类在总数据集中占比
p1 = p.count(class_val) / size
score += p1 * p1 # gini index formula = 1 - sum(p_i^2)
# 计算总的基尼指数,权重:当前分组占总数据集中的数量
gini += (1.0 - score) * (size / n_instances)
return gini
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1): # 最后分类不计算
for row in dataset:
# 根据每个值分类计算出最优基尼值,这个值就作为决策树的节点
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
print('X%d < %.3f Gini=%.3f' % ((index+1), row[index], gini))
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
dataset = [
[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]
]
split = get_split(dataset)
print('Split: [X%d < %.3f]' % ((split['index']+1), split['value']))
通过执行结果可以看出,X1 < 6.642 Gini=0.000 基尼指数为 0.0 为完美分割。
构建树主要分为 3 个部分
- 终端节点
Terminal Nodes零度节点称为终端节点或叶节点 - 递归拆分
- 建造一棵树
需要决定何时停止种植树,这里可以使用节点在训练数据集中负责的深度和行数来做到。
- 树的最大深度:从树的根节点开始的最大节点数。一旦达到树的最大深度,停止拆分新节点。
- 最小节点:对一个节点的要训练的最小值。一旦达到或低于此最小值,则停止拆分和添加新节点。
这两种方法将是构建树的过程时用户的指定参数。当在给定点停止增长时,该节点称为终端节点,用于进行最终预测。
编写一个函数to_terminal(),这个函数将为一组行选择一类。它返回行列表中最常见的输出值。
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
构建决策树会在为每个节点创建的组上一遍又一遍地调用 get_split() 函数。
添加到现有节点的新节点称为子节点。一个节点可能有零个子节点(一个终端节点)、一个子节点或两个子节点,这里将在给定节点的字典表示中将子节点称为左和右。当一旦创建出一个节点,则通过再次调用相同的函数来递归地从拆分的每组数据以创建子节点。
下面需要实现这个过程(递归函数)。函数接受一个节点作为参数,以及节点中的最大深度、最小模式数、节点的当前深度。
调用的过程分步为。设置,传入根节点和深度1:
- 首先,将拆分后的两组数据提取出来使用,当处理过这些组时,节点不再需要访问这些数据。
- 接下来,我们检查左或右两组是否为空,如果是,则使用我们拥有的记录创建一个终端节点。
- 不为空的情况下,检查是否达到了最大深度,如果是,则创建一个终端节点。
- 然后我们处理左子节点,如果行组太小,则创建一个终端节点,否则以深度优先的方式创建并添加左节点,直到在该分支上到达树的底部。最后再以相同的方式处理右侧。
# 创建子拆分或者终端节点
def split(node, max_depth, min_size, depth):
"""
:param node: {},分割好的的{'index':b_index, 'value':b_value, 'groups':b_groups}
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:param depth:int, 当前深度
:return: None
"""
left, right = node['groups']
del(node['groups'])
# 检查两边的分割问题
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# 检查最大的深度
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# 处理左分支,数量要小于最小模式数为terminal node
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1) # 否则递归
# 处理左右支,数量要小于最小模式数为terminal node
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
构建一个树就是一个上面的步骤的合并,通过split()函数打分并确定树的根节点,然后通过递归来构建出整个树;下面代码是实现此过程的函数 build_tree()。
# Build a decision tree
def build_tree(train, max_depth, min_size):
"""
:param train: list, 数据集,可以是训练集
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:return: None
"""
root = get_split(train) # 对整个数据集进行打分
split(root, max_depth, min_size, 1)
return root
将全部代码整合为一个
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculate the Gini index for a split dataset
def gini_index(groups, classes):
# 计算两组数据集的总数每个种类的列表数量和
n_instances = float(sum([len(group) for group in groups]))
# 计算每组的基尼值
gini = 0.0
for group in groups:
size = float(len(group))
# avoid divide by zero
if size == 0:
continue
score = 0.0
# score the group based on the score for each class
for class_val in classes:
# 拿出数据集中每行的类型,拆开是为了更好的了解结构
p = [row[-1] for row in group]
# print("%f / %f = %f" % (p.count(class_val), size, p.count(class_val) / size ))
# 这里计算的是当前的分类在总数据集中占比
p1 = p.count(class_val) / size
score += p1 * p1 # gini index formula = 1 - sum(p_i^2)
# 计算总的基尼指数,权重:当前分组占总数据集中的数量
gini += (1.0 - score) * (size / n_instances)
return gini
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1): # 最后分类不计算
for row in dataset:
# 根据每个值分类计算出最优基尼值,这个值就作为决策树的节点
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
# print('X%d < %.3f Gini=%.3f' % ((index+1), row[index], gini))
if gini < b_score: # 拿到最小的gini index那列
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
# 创建子拆分或者终端节点
def split(node, max_depth, min_size, depth):
"""
:param node: {},分割好的的{'index':b_index, 'value':b_value, 'groups':b_groups}
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:param depth:int, 当前深度
:return: None
"""
left, right = node['groups']
del(node['groups'])
# 检查两边的分割问题
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# 检查最大的深度
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# 处理左分支,数量要小于最小模式数为terminal node
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1) # 否则递归
# 处理左右支,数量要小于最小模式数为terminal node
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
# Build a decision tree
def build_tree(train, max_depth, min_size):
"""
:param train: list, 数据集,可以是训练集
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:return: None
"""
root = get_split(train) # 对整个数据集进行打分
split(root, max_depth, min_size, 1)
return root
# 打印树
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ( (depth*' ', (node['index']+1), node['value']) ))
print_tree(node['left'], depth+1) # 递归打印左右
print_tree(node['right'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node))) # 不是对象就是terminal node
# 创建一个terminal node
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
dataset = [
[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]
]
if __name__=='__main__':
tree = build_tree(dataset, 4, 2)
print_tree(tree)
可以看到打印结果是一个类似二叉树的
[X1 < 6.642]
[X1 < 2.771]
[0]
[X1 < 2.771]
[0]
[0]
[X1 < 7.498]
[X1 < 7.445]
[1]
[1]
[X1 < 7.498]
[1]
[1]
预测是预测数据是该向右还是向左,是作为对数据进行导航的方式。这里可以使用递归来实现,其中使用左侧或右侧子节点再次调用相同的预测,具体取决于拆分如何影响提供的数据。
我们必须检查子节点是否是要作为预测返回的终端值,或者它是否是包含要考虑的树的另一个级别的字典节点。
下面是实现此过程的函数 predict()。
# Make a prediction with a decision tree
def predict(node, row):
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row)
else:
return node['left']
else:
if isinstance(node['right'], dict):
return predict(node['right'], row)
else:
return node['right']
下面是一个使用硬编码决策树的示例,该决策树具有一个最好地分割数据的节点(决策树桩,这个就是gini index的最优质值)。通过对上面的测试数据集例来对每一行进行预测。
def predict(node, row):
# 如果gini index与对应属性的值小于则向左,
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row) # 递归处理完整个树
else:
return node['left']
else: # 否则的话,则为右
if isinstance(node['right'], dict):
return predict(node['right'], row)
else:
return node['right']
dataset = [[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]]
# 这是之前用于计算出最优的gini index
stump = {'index': 0, 'right': 1, 'value': 6.642287351, 'left': 0}
for row in dataset:
prediction = predict(stump, row)
print('Expected=%d, Got=%d' % (row[-1], prediction))
通过观察可以看出预测结果和实际结果一样
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
这里将使用 CART 算法对银行钞票数据集进行预测。大概的流程为:
- 加载数据集并转换格式。
- 编写拆分算法与准确度计算算法;这里使用 5折的k折交叉验证(
k-fold cross validation)用于评估算法 - 编写 CART 算法,从训练数据集,创建树,对测试数据集进行预测操作
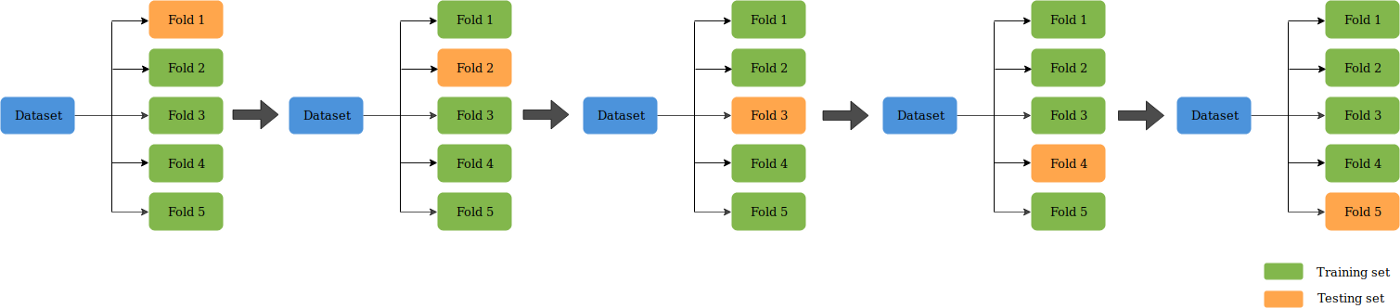
K折较差验证(K-Fold CV)是将给定的数据集分成K个部分,其中每个折叠在某时用作测试集。以 5 折(K=5)为例。这种情况下,数据集被分成5份。在第一次迭代中,第一份用于测试模型,其余用于训练模型。在第二次迭代中,第 2 份用作测试集,其余用作训练集。重复这个过程,直到 5 个折叠中的每个折叠都被用作测试集。
下面来开始编写函数,函数的整个过程为
evaluate_algorithm()作为最外层调用- 使用五折交叉进行评估
cross_validation_split() - 使用决策树算法作为算法根据
decision_tree() - 构建树:
build_tree()- 拿到最优基尼指数作为叶子
get_split()
- 拿到最优基尼指数作为叶子
- 使用五折交叉进行评估
from random import seed
from random import randrange
from csv import reader
# 加载csv文件
def load_csv(filename):
file = open(filename, "rt")
lines = reader(file)
dataset = list(lines)
return dataset
# 将所有字段转换为float类型便于计算
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# k-folds CV函数
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
# 平均分位折数n_folds
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy)) # 随机
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# 计算精确度
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# 根据基尼指数划分value是应该在树的哪边?
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# 基尼指数打分
def gini_index(groups, classes):
# 计算数据集中的多组数据的总个数
n_instances = float(sum([len(group) for group in groups]))
# 计算每组中的最优基尼指数
gini = 0.0
for group in groups:
size = float(len(group))
if size == 0:
continue
score = 0.0
# 总基尼指数
for class_val in classes:
# 拿出数据集中每行的类型,拆开是为了更好的了解结构
# 计算的是当前的分类在总数据集中占比
p = [row[-1] for row in group]
p1 = p.count(class_val) / size
score += p1 * p1
# 计算总的基尼指数,并根据相应大小增加权重。权重:当前分组占总数据集中的数量
gini += (1.0 - score) * (size / n_instances)
return gini
# 从数据集中获得基尼指数最佳的值
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
# 创建终端节点
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
# 创建子节点,为终端节点或子节点
def split(node, max_depth, min_size, depth):
"""
:param node: {},分割好的的{'index':b_index, 'value':b_value, 'groups':b_groups}
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:param depth:int, 当前深度
:return: None
"""
left, right = node['groups']
del(node['groups'])
# check for a no split
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# check for max depth
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# process left child
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1)
# process right child
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
# 构建树
def build_tree(train, max_depth, min_size):
"""
:param train: list, 数据集,可以是训练集
:param max_depth: int, 最大深度
:param min_size:int,最小模式数
:ret
"""
root = get_split(train)
split(root, max_depth, min_size, 1)
return root
# 打印树
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ( (depth*' ', (node['index']+1), node['value']) ))
print_tree(node['left'], depth+1) # 递归打印左右
print_tree(node['right'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node))) # 不是对象就是terminal node
# 预测,预测方式为当前基尼指数与最优基尼指数相比较,然后放入树两侧
def predict(node, row):
"""
:param node: {} 叶子值
:param row: {}, 需要预测值
:ret
"""
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row)
else:
return node['left']
else:
if isinstance(node['right'], dict):
return predict(node['right'], row)
else:
return node['right']
def decision_tree(train, test, max_depth, min_size):
tree = build_tree(train, max_depth, min_size)
predictions = list()
for row in test:
prediction = predict(tree, row)
predictions.append(prediction)
return(predictions)
# Test CART on Bank Note dataset
seed(1)
# 加载数据
filename = 'data_banknote_authentication.csv'
dataset = load_csv(filename)
# 转换格式
for i in range(len(dataset[0])):
str_column_to_float(dataset, i)
# 评估算法
n_folds = 5
max_depth = 5
min_size = 10
scores = evaluate_algorithm(dataset, decision_tree, n_folds, max_depth, min_size)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
Reference
Informatioin Gain
implement decision tree algorithm
inplement information gain
