【以下内容仅为本人在做题学习中的所感所想,本人水平有限目前尚处学习阶段,如有错误及不妥之处还请各位大佬指正,请谅解,谢谢!】
!!!观前提醒!!!
【本文篇幅较大,如有兴趣建议分段阅读】
有关二分查找
作用:在有序集合中快速查找目标值
适用性:
1. 只能查找有序的数据集
顺序存储的数据结果就是数组了,也就是二分查找只能从数组中查找,而不能查找链式存储的数据集,比如查找链表中的数,就不能用二分查找。
2. 针对的是静态有序数据集
二分查找适合那种不经常变动的数据集合。如果经常插入、删除的数据集,每次插入和删除都要保证集合数据的有序,维护动态数据有序的成本很高。所以二分查找适合从有序的不经常变动的数据集合中查找。适合数据集合已经排好序,但是需要经常查找的场景。
3. 不适合数据量太大或者太小的场景
因为二分查找需要依赖数组这种数据结构,而数组要求连续的内存空间,其需要把所有数据全部读入内存中,因此数据量太大的,对内存要求比较高。如果数据量只有几十个,那么不论是使用二分查找还是顺序遍历,查找效率都差不多。
有关二分查找的边界问题
“思路很简单,细节是魔鬼”
二分的几个常用情景:寻找一个数、寻找左侧边界、寻找右侧边界
以下是二分查找的基本框架:
1 public int BinarySearch(int[] nums, int target) { 2 int left = 0, right = ...; 3 while(...) { 4 int mid = left + ((right - left) >> 1); 5 if (nums[mid] == target) { 6 ... 7 } else if (nums[mid] < target) { 8 left = ... 9 } else if (nums[mid] > target) { 10 right = ... 11 } 12 } 13 return ...; 14 }
分析二分查找的一个技巧是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节。
(一) 寻找一个数
1 public int BinarySearch(int[] nums, int target) { 2 int left = 0; 3 int right = nums.length - 1; //【1】 4 5 while(left <= right) { //【2】 6 int mid = left + ((right - left) >> 1); 7 if(nums[mid] == target) 8 return mid; 9 else if (nums[mid] < target) 10 left = mid + 1; //【3】 11 else if (nums[mid] > target) 12 right = mid - 1; //【4】 13 } 14 return -1; 15 }
1. while中的循环条件
循环条件由搜索区间的结构确定,当找到目标值后,返回即可;
若没找到则需考虑终止情况。此处的搜索区间的结构是两端闭区间。当left == right时,表示区间[left, right],此时区间内仍有一个数值未被搜索,若此时结束循环,可能错过对目标值的匹配,因此需要继续查找,则终止条件应当是left > right时,此时搜索区间为空。所以此处while中应当为“<=”。
如果要使用小于号,则在结尾加一句判断即可。
1 return nums[left] == target ? left : -1;
2. left与right的加加减减
边界的加减也由搜索区间的结构确定。在[left, right]中mid被检测后,需要据mid将其划分为两个区间,若mid位置上的值不等于target,则不用再考虑mid。因为边界均可取到,所以搜索区间因改为[left, mid – 1]或[mid + 1, right]
3. 缺点
当数据中重复出现目标元素,则返回的是在重复序列中中间位置的索引,并不能得到其左侧或右侧边界。如{1, 2, 2, 2, 3, 5},target = 2,此时返回索引为2,但其边界为[1, 3]
(二) 寻找左侧边界
1 public int LeftBound(int[] nums, int target) { 2 if (nums.length == 0) return -1; 3 int left = 0; 4 int right = nums.length; //【1】 5 6 while (left < right) { //【2】 7 int mid = left + ((left + right) >> 1); 8 if (nums[mid] == target) { 9 right = mid; //【3】 10 } else if (nums[mid] < target) { 11 left = mid + 1; 12 } else if (nums[mid] > target) { 13 right = mid; //【4】 14 } 15 } 16 return left; 17 }
1. while中的循环条件
同理,此处的搜索区间为左闭右开型,当left == right时,表示区间[left, right),此时的区间已经为空,故可以终止。
注:这里解释一下为何上面用两端闭区间,而这里用左开后闭区间。因为这样的写法比较普遍,不这么写也可以,后文将会展示三种写法(两端闭,左开右闭,左闭右开)。
2. left与right的加减
因为此处是左闭右开区间,在[left, right)中mid被检测后,需要据mid将其划分为两个区间,[left, mid)和[mid + 1, right)。为了保证区间结构不变,所以right应变为mid,left应变为mid + 1
3. 有关结尾的返回值
返回值表示目标值在序列中的左侧边界,等价于小于目标值的元素个数。分析可知left的取值范围是[0, nums.Length],所以当left == nums.Length时,说明没有一个元素小于target,即target在该序列中不存在,返回-1即可。(当然,最终的返回值也可以是right,因为终止条件是left == right)
1 if (left == nums.length) return -1; 2 return nums[left] == target ? left : -1;
4. 该算法的核心,即为何可以查找左侧边界
1 if (nums[mid] == target) 2 right = mid;
当nums[mid] == target时,因为数据有序,说明mid左侧可能存在target,所以应缩小上界,不断向左收缩。
5. 统一格式,将while循环加入等号
据原理,只需将right初值设为nums.Length – 1;right的变化改为mid – 1即可。
1 public int LeftBound(int[] nums, int target) { 2 int left = 0, right = nums.length - 1; 3 while (left <= right) { 4 int mid = left + (right - left) / 2; 5 if (nums[mid] == target) { 6 right = mid - 1; 7 left = mid + 1; 8 } else if (nums[mid] > target) { 9 right = mid - 1; 10 } else if (nums[mid] < target) { 11 left = mid + 1; 12 } 13 } 14 if (left >= nums.length || nums[left] != target) 15 return -1; 16 return left; 17 }
(三) 寻找右边界
1 public int RightBound(int[] nums, int target) { 2 if (nums.length == 0) return -1; 3 int left = 0, right = nums.length; 4 while (left < right) { 5 int mid = left + ((left + right) >> 1); 6 if (nums[mid] == target) { 7 left = mid + 1; //【1】 8 } else if (nums[mid] < target) { 9 left = mid + 1; 10 } else if (nums[mid] > target) { 11 right = mid; 12 } 13 } 14 return left - 1; //【2】 15 }
1. left与right的加减
因为此处是左闭右开区间,在[left, right)中mid被检测后,需要据mid将其划分为两个区间,[left, mid)和[mid + 1, right) 。为了保证区间结构不变,所以right应变为mid,left应变为mid + 1
2. 有关最后返回值
因为对left的更新为mid + 1,结束时会产生以下结果:
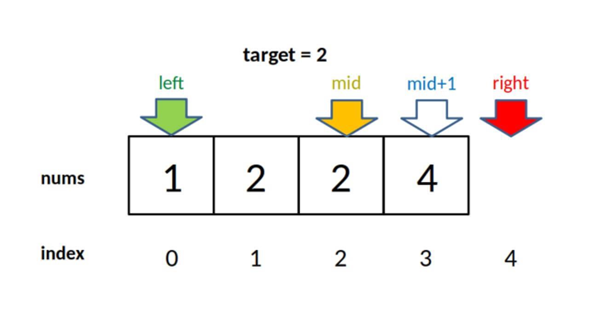
[注:上图来源于搜索引擎查找结果】
所以需返回left – 1(也可返回right - 1)。
同理,当left == 0时,说明没有一个元素大于target,即target在该序列中不存在,返回-1即可。
1 if (left == 0) return -1; 2 return nums[left-1] == target ? (left-1) : -1;
3. 统一格式
1 public int RightBound(int[] nums, int target) { 2 int left = 0, right = nums.length - 1; 3 while (left <= right) { 4 int mid = left + ((right - left) >> 1); 5 if (nums[mid] == target) { 6 left = mid + 1; 7 } else if (nums[mid] > target) { 8 right = mid - 1; 9 } else if (nums[mid] < target) { 10 left = mid + 1; 11 } 12 } 13 if (right < 0 || nums[right] != target) 14 return -1; 15 return right; 16 }
小结
1. 写二分查找时,尽量不要出现 else,将所有情况列出来便于分析。
2. 注意搜索区间形式和 while 的终止条件,若存在漏掉的元素,最后特判。
3. 如需定义左闭右开的搜索区间,搜索左右边界,只要在 nums[mid] == target 时做修改即可,搜索右侧时需要减一。
4. 如果将搜索区间全都统一成两端闭,只要修改 nums[mid] == target 条件处的代码和返回的逻辑即可。
从一维二分谈起
二分法,用于在集合中查找某些符合要求的元素,可以将时间复杂度降低至对数级。使用二分法的前提是查找序列的有序性,主要思想是从序列中间位置开始,根据当前的中间值与目标值的大小关系,修改区间端点,确定目标值所在区间。
- 题一:搜索旋转排序数组 33. 搜索旋转排序数组 - 力扣(LeetCode)
题意:在半有序的结合中查找目标元素的索引值
思想:选定中点,比较中点值来更改区间,但需要先判断当前所查找的区间是否为有序区间,否则不能使用二分法
1 //C# Version 2 3 public class Solution { 4 public int Search(int[] nums, int target) { 5 int n = nums.Length; 6 if(n == 0) return -1; 7 if(n == 1) return nums[0] == target ? 0 : -1; 8 9 int left = 0, right = n - 1; 10 while(left <= right) { 11 int mid = left + ((right - left) >> 1); 12 if(target == nums[mid]) return mid; 13 if(nums[0] <= nums[mid]) { 14 if(nums[0] <= target && target < nums[mid]) right = mid - 1; 15 else left = mid + 1; 16 } 17 else if(nums[0] > nums[mid]){ 18 if(nums[mid] < target && target <= nums[n - 1]) left = mid + 1; 19 else right = mid - 1; 20 } 21 } 22 return -1; 23 } 24 }
1 //C++ Version 2 3 class Solution { 4 public: 5 int search(vector<int>& nums, int target) { 6 int n = (int)nums.size(); 7 if(n == 0) return -1; 8 if(n == 1) return nums[0] == target ? 0 : -1; 9 10 int left = 0, right = n - 1; 11 while(left <= right) { 12 int mid = left + ((right - left) >> 1); 13 if(target == nums[mid]) return mid; 14 if(nums[0] <= nums[mid]) { 15 if(nums[0] <= target && target < nums[mid]) right = mid - 1; 16 else left = mid + 1; 17 } 18 else if(nums[0] > nums[mid]){ 19 if(nums[mid] < target && target <= nums[n - 1]) left = mid + 1; 20 else right = mid - 1; 21 } 22 } 23 return -1; 24 } 25 };
- 题二:长度最小的子数组 209. 长度最小的子数组 - 力扣(LeetCode)
题意:找出数组中满足其和大于等于目标值的长度最小的连续子序列
思想:要判断连续区间内的和,就先求出原数组的前缀和,因为题保证了数组中每个元素都为正,所以前缀和一定是递增的,保证了二分的正确性。
得到前缀和之后,对于每个开始下标 i,可通过二分查找得到大于或等于i的最小下标 bound,使得 sum[bound] - sum [i−1] ≥ target,并更新子数组的最小长度,此时子数组的长度是bound - i + 1。
【注:此解法非最优解】
1 //C# Version 2 3 public class Solution { 4 public int MinSubArrayLen(int target, int[] nums) { 5 int n = nums.Length; 6 if (n == 0) return 0; 7 int ans = int.MaxValue; 8 int[] sums = new int[n + 1]; 9 for (int i = 1; i <= n; ++i) 10 sums[i] = sums[i - 1] + nums[i - 1]; 11 for (int i = 1; i <= n; ++i) { 12 int s = target + sums[i - 1]; 13 int bound = LowerBound(sums, i, n - 1, s); 14 if (bound != -1) 15 ans = Math.Min(ans, bound - i + 1); 16 } 17 return ans == int.MaxValue ? 0 : ans; 18 } 19 private int LowerBound(int[] nums, int left, int right, int s) { 20 while (left <= right) { 21 int mid = left + ((right - left) >> 1); 22 if (nums[mid] < s) left = mid + 1; 23 else right = mid - 1; 24 } 25 return (nums[left] >= s) ? left : -1; 26 } 27 }
1 //C++ Version 2 3 class Solution { 4 public: 5 int minSubArrayLen(int s, vector<int>& nums) { 6 int n = nums.size(); 7 if (n == 0) return 0; 8 int ans = INT_MAX; 9 vector<int> sums(n + 1, 0); 10 for (int i = 1; i <= n; i++) 11 sums[i] = sums[i - 1] + nums[i - 1]; 12 for (int i = 1; i <= n; i++) { 13 int target = s + sums[i - 1]; 14 auto bound = lower_bound(sums.begin(), sums.end(), target); 15 if (bound != sums.end()) 16 ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1))); 17 } 18 return ans == INT_MAX ? 0 : ans; 19 } 20 };
- 题三:寻找峰值 162. 寻找峰值 - 力扣(LeetCode)
题意:找到数组中某个峰值元素的索引(且nums[-1]与nums[len] = 负无穷)
思想:首先思考如何判断峰值所在区间。
假设mid < mid + 1
- 对于mid – 1,无论是mid – 1 > mid还是mid – 1 > mid均不能得到mid是峰值;
- 对于mid + 2,有两种情况:若mid + 2 < mid + 1则峰值为mid + 1;若mid + 2 > mid + 1,继续后推,由于边界后的值为-∞,那么一定可以得到最后一个值为峰值。
综上:峰值一定在较大的一部分。
1 //C# Version 2 3 public class Solution { 4 public int FindPeakElement(int[] nums) { 5 int left = 0, right = nums.Length - 1; 6 while(left < right) 7 { 8 int mid = left + (right - left) / 2; 9 if(nums[mid] > nums[mid + 1]) right = mid; 10 else left = mid + 1; 11 } 12 return left; 13 } 14 }
1 //C++ Version 2 3 int findPeakElement(vector<int>& nums) { 4 int left = 0, right = nums.size() - 1; 5 for (; left < right; ) { 6 int mid = left + (right - left) / 2; 7 if (nums[mid] > nums[mid + 1]) { 8 right = mid; 9 } else { 10 left = mid + 1; 11 } 12 } 13 return left; 14 }
小结
一维二分思想和操作较为简单,具体步骤为:
1. 确定并构建查找对象。即是查找元素,还是查找和、差等,构建出用于查找的序列,如:前缀和。
2. 判断二分后目标值可能的所在区间。一般是通过中值和目标值的比较更改区间,特殊地(如峰值寻找)需要运用一定数学知识进行判断。
有关二维二分
二维本质上可以看作是一维的叠加,某些简单的情况下,可以一维一维的查找。也可以从定义出发,从中点开始进行区间更改。当然,二维二分也有一些常见的变式,如从一个端点、对角线两个端点出发等。
- 题一:搜索二维矩阵 74. 搜索二维矩阵 - 力扣(LeetCode)
题意:在二维矩阵中查找某个值是否存在。
思想:可以将二维数组划分为一维数组,一行一行或一列一列进行判断。可以对矩阵的第一列的元素二分查找,找到最后一个不大于目标值的元素,然后在该元素所在行,进行二分查找目标值是否存在。
1 //C# Version 2 3 class Solution { 4 public bool SearchMatrix(int[][] matrix, int target) { 5 int rowIndex = BinarySearchFirstColumn(matrix, target); 6 if (rowIndex < 0) return false; 7 return BinarySearchRow(matrix[rowIndex], target); 8 } 9 10 private int BinarySearchFirstColumn(int[][] matrix, int target) { 11 int low = -1, high = matrix.Length - 1; 12 while (low < high) { 13 int mid = (high - low + 1) / 2 + low; 14 if (matrix[mid][0] <= target) low = mid; 15 else high = mid - 1; 16 } 17 return low; 18 } 19 20 private bool BinarySearchRow(int[] row, int target) { 21 int low = 0, high = row.Length - 1; 22 while (low <= high) { 23 int mid = (high - low) / 2 + low; 24 if (row[mid] == target) return true; 25 else if (row[mid] > target) high = mid - 1; 26 else low = mid + 1; 27 } 28 return false; 29 } 30 }
也可以从定义出发,从中间点开始进行判断。
1 //C# Version 2 3 public class Solution { 4 public bool SearchMatrix(int[][] matrix, int target) { 5 int m = matrix.Length, n = matrix[0].Length; 6 int low = 0, high = m * n - 1; 7 while (low <= high) { 8 int mid = low + ((high - low) >> 1); 9 int x = matrix[mid / n][mid % n]; 10 if (x < target) low = mid + 1; 11 else if (x > target) high = mid - 1; 12 else return true; 13 } 14 return false; 15 } 16 }
注意到每行的第一个整数大于前一行的最后一个整数。因此,把每一行拼接到前一行可以得到一个递增序列,所以可以从右上角开始进行判断。
1 //C# Version 2 3 public class Solution { 4 public bool SearchMatrix(int[][] matrix, int target) { 5 int n = matrix.Length; 6 if(n == 0) return false; 7 int row = 0, col = matrix[0].Length - 1; 8 while(row < n && col >= 0) 9 { 10 if(matrix[row][col] < target) row++; 11 else if(matrix[row][col] >target) col--; 12 else return true; 13 } 14 return false; 15 } 16 }
1 //C++ Version 2 3 class Solution { 4 public: 5 bool searchMatrix(vector<vector<int>>& matrix, int target) { 6 int row = matrix.size(), col = matrix[0].size(); 7 for(int i = 0, j = col-1; i < row && j >= 0;) { 8 if(matrix[i][j] == target) 9 return true; 10 else if(matrix[i][j] > target) 11 j--; 12 else if(matrix[i][j] < target) 13 i++; 14 } 15 return false; 16 } 17 };
- 题二:有序矩阵中的第K小的元素 378. 有序矩阵中第 K 小的元素 - 力扣(LeetCode)
题意:在矩阵中找到第K小数
思想:可以从定义出发,从中间点开始进行判断。关键是统计对于当前数mid,有多少个比它小的数。
若每行的第一个整数大于前一行的最后一个整数,则cnt = i * n + j。但本题不满足该条件,则需要寻找一个参照值,通过循环,统计小于等于当前值的元素数。观察四个边角,左上角的元素最小,右下角的元素最大,而左下角和右上角的元素大小与mid相比是未定的,不妨取二者其一作为参照值。
在此,取左下角的值为参照值。
1 //C# Version 2 3 public class Solution { 4 public int KthSmallest(int[][] matrix, int k) { 5 int n = matrix.Length; 6 int left = matrix[0][0], right = matrix[n - 1][n - 1]; 7 while(left < right) { 8 int mid = left + ((right - left) >> 1); 9 if(Check(matrix, mid, k, n)) right = mid; 10 else left = mid + 1; 11 } 12 return left; 13 } 14 private bool Check(int[][] matrix, int mid, int k, int n) { 15 int cnt = 0; 16 int i = n - 1, j = 0; 17 while(i >= 0 && j < n) { 18 if(matrix[i][j] > mid) i--; 19 else { 20 cnt += i + 1; 21 j++; 22 } 23 } 24 return cnt >= k; 25 } 26 }
- 题三 乘法表中第K小数 668. 乘法表中第k小的数 - 力扣(LeetCode)
本题与上题类似,只是在计数上有变化。
1 /C# Version 2 3 public class Solution { 4 public int FindKthNumber(int m, int n, int k) { 5 int left = 1, right = m * n; 6 while(left < right) { 7 int mid = left + ((right - left) >> 1); 8 if(CheckCnt(mid, k, m, n)) right = mid; 9 else left = mid + 1; 10 } 11 return left; 12 } 13 private bool CheckCnt(int mid, int k, int m, int n) { 14 int cnt = 0; 15 for(int i = 1; i <= m; i++) cnt += Math.Min(mid / i, n); 16 return cnt >= k; 17 } 18 }
小结
二维二分通常从边角出发,通常以边角值为参照值,进行区间的更新。其本质依旧是比大小,改区间。
有关第K小数
在此介绍一种算法:中位数的中位数算(BFPRT),该算法主要解决TOP-K问题。
有一个经典的问题,“从长度为N的无序数组中找出前k大的数”。TOP-K问题的最简单解法为快速排序后取第K大的数,但快速排序可能会达到最坏情况时间复杂度O(n2),且会对无用的数据进行排序操作(归并除外)。而该算法的主要优化是,修改快速排序选择主元的方法,优化最坏时间复杂度。
对于快速排序,一般选择中间位置的元素作为参照值,将小的数移到参照值左边,大的数移到右边,此时对于中间位置的该值,即为序列中第n/2小的数。
那么,是否可以用类似的方法,通过一次O(n)的操作找出第k小数呢?
该算法通过“随机选择”实现了这个操作,其思想与快排类似,仅仅改变了对参照值的选取。
具体流程:
1.将n个元素划为 n/5 组,每组5个,至多只有一组由 n%5 个元素组成。
2.寻找每一个组的中位数(可以用插排)。
3.对步骤2选出的 n/5 个中位数,重复步骤1和步骤2,递归下去,直到剩下一个数字。
4.最终剩下的数字近似为序列的中位数pivot,把小于等于它的数放左边,大于的数放右边。
5.判断pivot的位置与k的大小,如果pivot > k,则在[0, pivot – 1]内寻找第k小数;反之在[pivot + 1, n - 1]内寻找 k – pivot 小的数。
注意下面两种分治的思想:
1.分治法O(nlogn):大问题分解为小问题,小问题都要递归各个分支,例如:快速排序。
2.减治法O(n):大问题分解为小问题,小问题只要递归一个分支,例如:二分查找,随机选择。
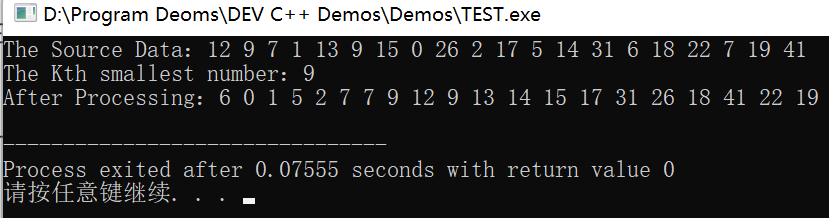
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int InsertSort(int array[], int left, int right); 5 int GetPivotIndex(int array[], int left, int right); 6 int Partition(int array[], int left, int right, int pivot_index); 7 int BFPRT(int array[], int left, int right, int k); 8 9 ///划分 10 int Partition(int arr[], int left, int right, int pivot_index) { 11 swap(arr[pivot_index], arr[right]); // 把主元放置于末尾 12 13 int partition_index = left; // 跟踪划分的分界线 14 for (int i = left; i < right; i++) 15 if (arr[i] < arr[right]) 16 swap(arr[partition_index++], arr[i]); // 比pivot小的都放在左侧 17 18 swap(arr[partition_index], arr[right]); // 最后把pivot换回来 19 return partition_index; 20 } 21 22 ///返回第 k 小数的下标 23 int BFPRT(int arr[], int left, int right, int k) { 24 int pivot_index = GetPivotIndex(arr, left, right); // 得到中位数的中位数下标 25 int partition_index = Partition(arr, left, right, pivot_index); // 进行划分,返回划分边界 26 int num = partition_index - left + 1; 27 28 if (num == k) 29 return partition_index; 30 else if (num > k) 31 return BFPRT(arr, left, partition_index - 1, k); 32 else 33 return BFPRT(arr, partition_index + 1, right, k - num); 34 } 35 36 ///返回 [left, right]的中位数。 37 int Insertion(int arr[], int left, int right) { 38 int temp, j; 39 for (int i = left + 1; i <= right; i++) { 40 temp = arr[i]; 41 j = i - 1; 42 while (j >= left && arr[j] > temp) { 43 arr[j + 1] = arr[j]; 44 j--; 45 } 46 arr[j + 1] = temp; 47 } 48 return left + ((right - left) >> 1); 49 } 50 51 ///数组每五个元素作为一组,并计算每组的中位数,最后返回这些中位数的中位数下标 52 ///末尾返回语句最后一个参数多加 1 的作用是向上取整,可以始终保持 k 大于 0。 53 int GetPivotIndex(int arr[], int left, int right) { 54 if (right - left < 5) 55 return Insertion(arr, left, right); 56 int sub_right = left - 1; 57 58 // 每五个作为一组,求出中位数,并把这些中位数全部依次移动到数组左边 59 for (int i = left; i + 4 <= right; i += 5) { 60 int index = Insertion(arr, i, i + 4); 61 swap(arr[++sub_right], arr[index]); 62 } 63 64 // 利用 BFPRT 得到这些中位数的中位数下标 65 return BFPRT(arr, left, sub_right, ((sub_right - left + 1) >> 1) + 1); 66 } 67 68 int main() { 69 ios::sync_with_stdio(false); 70 int k = 8; // 1 <= k <= array.size 71 int nums[20] = { 12, 9, 7, 1, 13, 9, 15, 0, 26, 2, 17, 5, 14, 31, 6, 18, 22, 7, 19, 41 }; 72 73 cout << "The Source Data:"; 74 for (int i = 0; i < 20; i++) 75 cout << nums[i] << " "; 76 cout << endl; 77 78 // 因为是以 k 为划分,所以还可以求出第 k 小值 79 cout << "The Kth smallest number:" << nums[BFPRT(nums, 0, 19, k)] << endl; 80 81 cout << "After Processing:"; 82 for (int i = 0; i < 20; i++) 83 cout << nums[i] << " "; 84 cout << endl; 85 return 0; 86 }